Lineare Approximation
Nehmen wir an, Sie haben eines Tages einen Taschenrechner vergessen und möchten wirklich herausfinden, wie die Quadratwurzel von 2 ist. Wie würden wir ohne Taschenrechner herausfinden? Wir können lineare Annäherung verwenden!
Linearisierung einer Funktion
Bei der Linearisierung einer Funktion geht es nur darum, die Tangente der Funktion an einem bestimmten Punkt anders zu finden., Die Linearisierungsformel lautet:

wobei L (x) die Gleichung der Tangente am Punkt a ist.
Wie ist das für uns nützlich? Nun, wir können diese Gleichung tatsächlich verwenden, um die Werte der Funktion in der Nähe von Punkt a zu approximieren.,
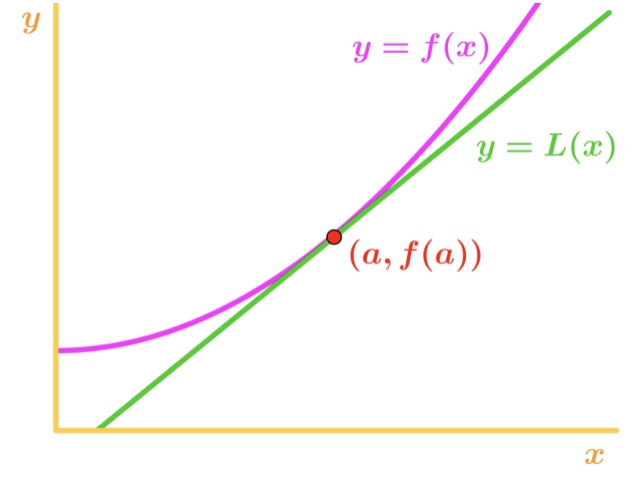
Beachten Sie, dass bei x-Werten in der Nähe von Punkt a die Funktion und die Tangentiallinie relativ nahe beieinander liegen. Aus diesem Grund können wir schreiben, dass die Funktion ungefähr gleich der Tangente in der Nähe von Punkt a ist., In anderen Worten,

wo ≈\approx≈ ist rund symbol. Diese Gleichung wird als lineare Näherungsformel bezeichnet. Es ist in gewissem Sinne linear, dass die Tangente eine gerade Linie ist, und wir verwenden sie, um die Funktion anzunähern. Mit dieser Annäherung können wir Werte annähern, die nicht von Hand gemacht werden können. Zum Beispiel kann die Quadratwurzel von 2 oder das natürliche Protokoll von 5 alle approximiert werden!, Eine wichtige Sache zu beachten ist, dass diese Approximation nur für x-Werte in der Nähe von Punkt a funktioniert. Wenn Sie einen x-Wert weit von Punkt a entfernt haben, wird die Approximation wirklich ungenau.
Schauen wir uns jetzt nicht ein paar Beispiele an, um die Linearisierung einer Funktion zu finden, und schauen uns dann an, wie man lineare Approximation verwendet!
Finden Sie die Linearisierung von L (x)der Funktion bei a
Frage 1: Betrachten Sie die Funktion
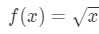
Angenommen, wir möchten die Linearisierung der Funktion an Punkt a=4 finden.
Um die Linearisierung L(x) zu finden, denken Sie daran, dass

- Schritt 1: Find a
- Schritt 2: Find f(a)
- Schritt 3: Find f'(a).
- Schritt 4: Stecken Sie alle drei in die Formel, um L (x)
-
Folgen wir diesen Schritten!,
Schritt 1: Zum Glück wird uns in der Frage a = 4 gegeben, also müssen wir nicht danach suchen.
- Schritt 2:
Beachten Sie, dass
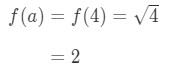
Gleichung 1: Linearisierung Frage pt. 3 - Schritt 3:
Wissen Sie, dass die Ableitung von Quadratwurzeln
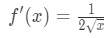
Gleichung 1: Linearisierungsfrage pt., 4 And so plugging in x=a gives us:
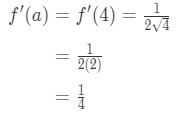
Equation 1: Linearization question pt. 5 - Step 4:
Since we know a, f(a), and f'(a), we can now plug it into L(x) to find the linearization of f(x).
Hence,
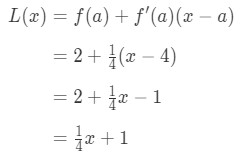
Equation 1: Linearization question pt., 6 Also L(x)=14\frac{1}{4}41x+1 ist die Linearisierung der Funktion an der Stelle x=4. Außerdem ist es auch die Tangente der Funktion am Punkt x=4.
Wie mache ich eine lineare Approximation
Denken Sie daran, dass wir früher gesagt haben, dass wir die Gleichung der Tangente verwenden könnten, um Werte der Funktion in der Nähe von a zu approximieren? Versuchen wir dies mit der Linearisierung, die wir zuvor gefunden haben. Daran erinnern, dass
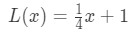
für Punkte in der Nähe von x=4. Wir können dies in eine lineare Näherung für f(x) ändern, indem wir Folgendes sagen:
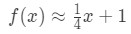
Angenommen, ich möchte f(4.04) annähern. Wenn Sie dies in die ursprüngliche Funktion einfügen würden ,würden Sie 4.04\sqrt{4.04}4.04. Ohne Taschenrechner wäre das wirklich schwer zu berechnen., Jedoch, durch lineare approximation, können wir sagen, dass

Diese Fragen gaben uns bisher eine Funktion und einen Punkt zum Arbeiten. Was wäre, wenn überhaupt keine davon gegeben würde? Was ist, wenn die Frage uns nur sagt, eine Zahl zu schätzen?
Verwenden Sie eine lineare Approximation, um eine Zahl zu schätzen
Angenommen, wir möchten 10\sqrt{10}10 schätzen. Wie würden wir es tun?, Wir müssten die lineare Approximation

aber wir haben nicht einmal eine Funktion und einen Punkt zum Arbeiten. Das heißt, wir müssen sie selbst machen. Dies führt uns zu den folgenden Schritten:
- Schritt 1: Erstellen Sie eine Funktion
- Schritt 2: Erstellen Sie Punkt a
- Schritt 3: Finden Sie f(a) und f'(a)
- Schritt 4: Stecken Sie alles in die lineare Näherungsformel
Folgen wir den Schritten!,
Frage 2: Schätzung 10\sqrt{10}10
- Schritt 1: Lassen Sie uns eine Funktion. Beachten Sie, dass wir schätzen
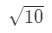
Gleichung 3: Schätzung mit linearen ca. pt.2 Wir müssen irgendwie eine Beziehung zwischen f(x) und 10 – \sqrt{10}10. Wir können nicht sagen, dass f(x) = 10\sqrt{10}10 da die Funktion nicht von x abhängig ist. Lassen
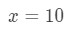
Gleichung 3: Rechnen mit linearen ca. pt.,3 Wenn wir das tun, dann sagen wir im Grunde
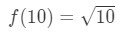
Gleichung 3: Schätzung mit linearen ca. pt.4 Wir können jetzt offensichtlich sagen, was die Funktion sein soll. Lassen
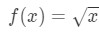
Gleichung 3: Rechnen mit linearen ca. pt.5 Wir haben also eine Funktion, aber jetzt brauchen wir einen Punkt a, mit dem wir arbeiten können.,
- Schritt 2:
Der Schlüssel zum Finden des richtigen Werts a besteht darin, zwei Dinge zu berücksichtigen:
1) Stellen Sie sicher, dass der Wert a nahe bei x
2) Stellen Sie sicher, dass f(a) eine schöne Zahl ist.
Wäre a = 8 ausreichend genug? Nun, 8 ist ziemlich nah an 10, also ist es nicht schlecht.
Gleichung 3: Schätzung mit linearen ca. pt.6 Beachten Sie, dass 8\sqrt{8}8 ist nicht eine sehr schöne Zahl. Tatsächlich erhalten Sie eine Reihe von Dezimalzahlen. Also müssen wir etwas anderes versuchen.,
Wäre a = 9 ausreichend genug? Auch hier ist 9 ziemlich nah an 10, also ist es okay. Auch,

Gleichung 3: Rechnen mit linearen ca. pt.7 f(a) ist eigentlich eine schöne ganze Zahl ist hier, also das tatsächlich funktioniert! Die Auswahl von a=9 ist also ausreichend.
- Schritt 3:
Beachten Sie, dass von früher:

Gleichung 3: Schätzung mit linearen ca. pt.,8 Calculating f'(x) we have again:

Equation 3: Estimate with linear approx. pt.9 So
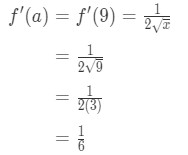
Equation 3: Estimate with linear approx. pt.,10 - Step 4:
Going back to the linear approximation formula we have:

Equation 3: Estimate with linear approx. pt.11 Plugging a, f(a), f'(a), f(x), and x in our formula you will see that:

Equation 3: Estimate with linear approx. pt.12 Hence, we just approximated the number!,
Wenn Sie mehr Praxisprobleme zur linearen Approximation wünschen, empfehle ich Ihnen, sich diesen Link hier anzusehen.
http://tutorial.math.lamar.edu/Classes/CalcI/LinearApproximations.aspx
Überschätzen und unterschätzen
Wir wissen, dass lineare Näherung nur eine Schätzung des Funktionswerts an einem bestimmten Punkt ist. Woher wissen wir das jedoch, wenn unsere Schätzung überschätzt oder unterschätzt wird? Wir berechnen die zweite Ableitung und betrachten die Konkavität.,
Konkav nach oben vs konkav nach unten
Wenn die zweite Ableitung der Funktion für Werte in der Nähe von a größer als 0 ist, ist die Funktion konkav nach oben. Dies bedeutet, dass unsere Annäherung eine Unterschätzung sein wird. In anderen Worten,
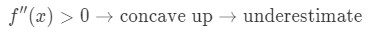
Warum? Schauen wir uns diese Grafik an.,
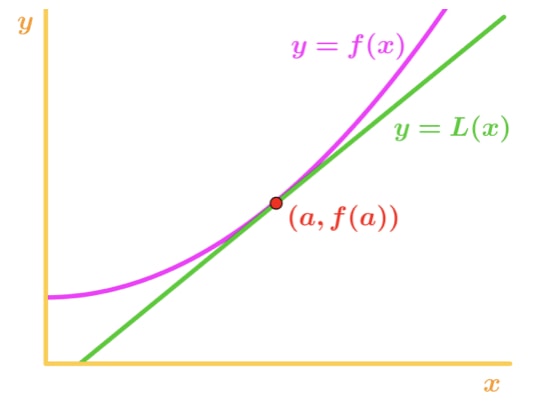
Beachten Sie, dass f(x) ist konkav nach oben und der Linie, direkt unter f(x). Nehmen wir an, wir sollten die Tangente verwenden, um f(x) zu approximieren. Dann sind die y-Werte der Tangente immer kleiner als der tatsächliche Wert von f(x). Daher haben wir eine Unterschätzung
Wenn nun die zweite Ableitung der Funktion für Werte in der Nähe von a kleiner als 0 ist,ist die Funktion konkav nach unten., Dies bedeutet, dass unsere Annäherung eine Überschätzung sein wird. Mit anderen Worten,
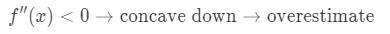
Warum? Schauen wir uns ein anderes Diagramm an.
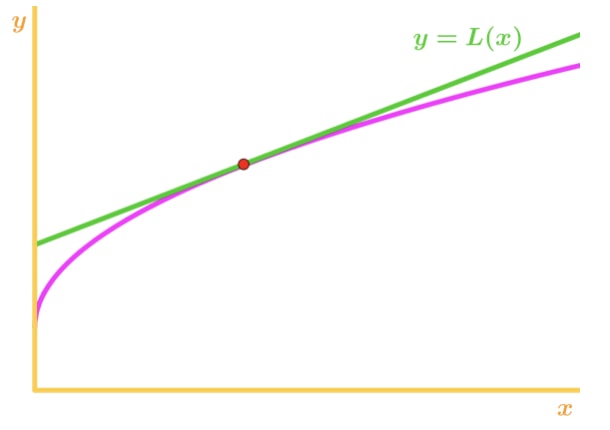
Beachten Sie, dass f(x) ist konkav nach unten und die Tangente ist rechts oben f(x). Nehmen wir noch einmal an, wir werden die Tangente verwenden, um f(x) zu approximieren., Dann werden die y-Werte der Tangente immer größer sein als der tatsächliche Wert von f (x). Daher haben wir eine Überschätzung.
Wenn Sie also jemals sehen müssen, ob Ihr Wert eine Unterschätzung oder eine Überschätzung ist, gehen Sie folgendermaßen vor:
- Schritt 1: Finden Sie die zweite Ableitung
- Schritt 2: Sehen Sie sich die Konkavität der Funktion in der Nähe von Punkt a
- Schritt 3: Bestätigen Sie, dass es sich um eine Unterschätzung/Überschätzung handelt
Schauen wir uns ein Beispiel an:
Frage 3: Sei f(x) = x\sqrt{x}x und a = 4. Wenn wir linear nähern f (4.,04), wäre es eine Überschätzung oder eine Unterschätzung?
- Schritt 1: Sehen Sie, dass
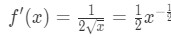
Gleichung 4: Frage überschätzen pt.1 Die zweite Ableitung lautet also
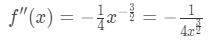
Gleichung 4: Frage überschätzen pt.2 - Schritt 2:
Beachten Sie, dass a=4 ist. Schauen Sie sich nun die zweite Ableitung an., Wenn x positiv ist, sehen wir, dass
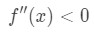
Gleichung 4: Überschätzen Frage pt.3 Daher ist es konkav nach unten
- Schritt 3:
Wir wissen, dass die Tangente über der Funktion liegt, wenn die Funktion konkav nach unten ist. Daher ergibt die Verwendung der Tangente als Näherung einen überschätzten Wert.
Differentiale
Wir können Werte nicht nur mit linearer Approximation approximieren, sondern auch mit Differentialen approximieren., Zur Annäherung verwenden wir die folgende Formel
wobei dy und dx Differentiale sind und f'(x) die Ableitung von f in Bezug auf x. Da es sich um sehr kleine Änderungen in x und y, dann werden wir die Tatsache verwenden, dass:
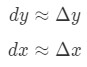
Die meisten Fragen, die wir stellen, betreffen jedoch die Einstellung
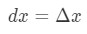
Die Verwendung dieser Fakten führt uns also zu:
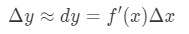
Diese Näherung ist sehr nützlich, wenn die Änderung von y angenähert wird., Denken Sie daran, damals hatten sie keine Rechner, also ist dies die beste Annäherung, die sie für Funktionen mit Quadratwurzeln oder natürlichen Protokollen bekommen konnten.
Die meiste Zeit müssen Sie selbst nach f'(x) und Δ\DeltaΔx suchen. Mit anderen Worten, folgen Sie diesen Schritten, um Δ\DeltaΔy zu approximieren!
- Schritt 1: Finden Δ \ DeltaΔx
- Schritt 2: Finden f'(x)
- Schritt 3: Stecker alles in die formel zu finden dy. dy ist die Näherung für Δ\DeltaΔy.
schauen wir uns ein Beispiel für die Verwendung dieser Näherung:
Frage 4: Betrachten Sie die Funktion y = ln(x + 1)., Angenommen, x ändert sich von 0 auf 0,01. Ungefähre Δ\DeltaΔy.
- Schritt 1: Beachten Sie, dass sich x von 0 auf 0,01 ändert, sodass die Änderung in x lautet:
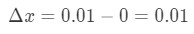
Gleichung 6: Differentialfrage pt.1 - Schritt 2:
Die Ableitung wäre:
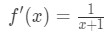
Gleichung 6: Differential Frage pt.,2 - Schritt 3:
Alles einstecken wir haben:
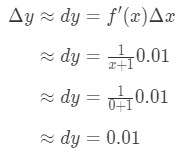
Gleichung 6: Differentialfrage pt.3 Daher Δ\DeltaΔy ≈\approx≈ 0.01
Wir möchten jedoch meistens einen Wert der Funktion und nicht die Änderung des Werts schätzen. Daher addieren wir beide Seiten der Gleichung um y, was uns Folgendes gibt:
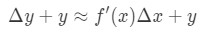
das ist das gleiche wie:
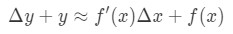
Diese Gleichung ist etwas schwer zu lesen, also werden wir sie noch mehr neu anordnen. Versuchen wir, y und Δ\DeltaΔy loszuwerden. Beachten Sie, dass Δ\DeltaΔy+ y im Grunde dasselbe ist wie das Finden des Werts der Funktion bei Δ\DeltaΔx+x. Mit anderen Worten,
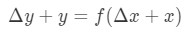
Wenn Sie dies in unserer obigen Annäherung ersetzen, erhalten wir:
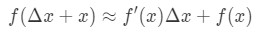
wobei f(Δ\DeltaΔx+x) der Wert ist, den wir schätzen möchten. Wie verwenden wir diese Formel? Ich empfehle folgende Schritte:
Lassen Sie uns diese Schritte für die folgende Frage verwenden.
Frage 5: Verwenden Sie Differentiale, um 10\sqrt{10}10 zu approximieren.
- Schritt 1: Vergleichen Sie f(Δ\DeltaΔx+x) mit 10 – \sqrt{10}10., Since 10\sqrt{10}10 has a square root and 9 is a perfect square that is closest to 10, then let
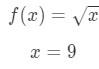
Equation 7: Approximate value with differentials pt.1 Notice that:
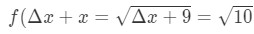
Equation 7: Approximate value with differentials pt.,2 Sehen Sie, dass es keine andere Wahl gibt, als Δ\DeltaΔx = 1
- Schritt 2:
Sehen Sie, dass die Ableitung Folgendes ergibt:

Gleichung 7: Ungefährer Wert mit Differentialen pt.3 Dies impliziert also
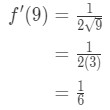
Gleichung 7: Ungefährer Wert mit Differentialen pt.,4 - Schritt 3:
das Stopfen alles in die Formel ergibt:
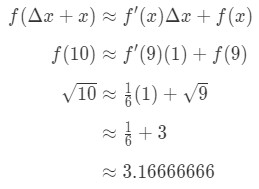
Gleichung 7: Ungefähre Wert Differentiale pt.5 Daher haben wir uns nur der Zahl angenähert.
Eine interessante Sache ist, dass lineare Näherung und Differentiale beide das gleiche Ergebnis für 10\sqrt{10}10 ergeben.,
Wenn Sie mehr über Differentiale erfahren möchten, klicken Sie auf diesen Link:
http://tutorial.math.lamar.edu/Classes/CalcI/LinearApproximations.aspx
L ‚ Hospitalregel mit linearer Approximation beweisen
Jetzt haben wir viel über lineare Approximation gelernt, aber was können wir sonst noch damit machen? Wir können tatsächlich die lineare Approximationsformel verwenden, um eine Regel zu beweisen, die als L ‚ Hospitalregel bekannt ist . Hier ist, wie der Beweis funktioniert.
Denken Sie daran, dass die lineare Näherungsformel lautet:

Sehen Sie, dass wir die Formel so anordnen können, dass:
Erkenne, dass die Näherung immer genauer wird, wenn wir x Werte auswählen, die näher an a liegen. Mit anderen Worten, wenn wir die Grenze als x→a nehmen, dann werden sie gleich. So
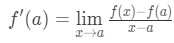
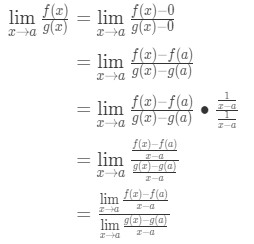
Beachten Sie nun, dass wir hier die Formel anwenden können, die wir zuvor abgeleitet haben. So, jetzt
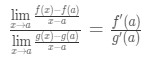
Anstatt nun f'(a) und g'(a) zu schreiben, können wir Grenzen als x→a anwenden (weil wir wissen, dass f und g unterscheidbar sind)., So
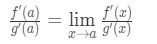
Daher haben wir gerade gezeigt, dass:
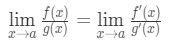
Das ist L ‚ Hospitalregel .
Wenn wir die l ‚hopital-Regel verwenden
Wir möchten immer die l‘ optial-Regel anwenden, wenn wir auf unbestimmte Grenzen stoßen. Es gibt zwei Arten von unbestimmten Formen., Diese unbestimmten Formen wären:
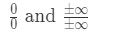
Viele Leute machen den Fehler, l ‚ hopitals Regel zu verwenden, ohne zu überprüfen, ob es sich um eine unbestimmte Grenze handelt. So stellen Sie sicher, dass Sie es zuerst überprüfen! Andernfalls funktioniert es nicht und Sie erhalten die falsche Antwort. Hier ist eine Anleitung zur Verwendung der l ‚ hopital-Regel:
- Schritt 1: Bewerten Sie das Limit direkt.
- Schritt 2: Überprüfen Sie, ob es sich um eine der unbestimmten Formen handelt. Wenn ja, gehen Sie zu Schritt 3.,
- Schritt 3: Verwenden Sie die l ‚ hopital-Regel.
- Schritt 4: Überprüfen Sie, ob Sie ein anderes unbestimmtes Formular erhalten. Wiederholen Sie Schritt 3, wenn Sie dies tun.
Schauen wir uns einige Beispiele mit diesen Schritten an.
Frage 6: Bewerten Sie die Grenze,
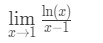
- Schritt 1: Auswertung der Grenze direkt gibt uns
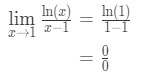
Gleichung 9: L’hopital ist Regel Frage pt.,2 - Schritt 2:
ja, es ist eine der unbestimmten Formen.
- Schritt 3:
Anwenden der l ‚hopital-Regel Wir haben:
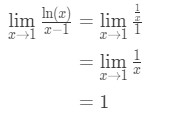
Gleichung 9: L ‚ hopitals Regelfrage pt.3 - Schritt 4:
Eins ist keine unbestimmte Form, also sind wir fertig und die Antwort ist 1.
Nun, diese Frage war ein bisschen einfach, also warum schauen wir uns nicht etwas an, das etwas schwieriger ist.,
Frage 7: Bewerten Sie die Grenze
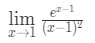
- Schritt 1: Das Limit direkt auswerten wir sehen, dass:
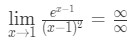
Gleichung 10: L ‚ hopitals Regel zweimal Frage pt.2 - Schritt 2:
Dies ist eine unbestimmte form, so gehen Sie zu Schritt 3.,
- Schritt 3:
Anwenden der l ‚hopital-Regel Wir haben
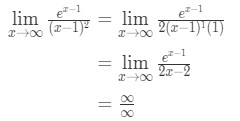
Gleichung 10: L ‚ hopitals Regel zweimal Frage pt.3 - Schritt 4:
Dies ist ein weiterer unbestimmter form. Wir müssen also zu Schritt 3 zurückkehren und l ‚ optials Regeln erneut anwenden.
- Schritt 3:
l ‚hopitals Regel erneut anwenden Wir haben:
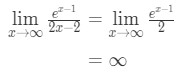
Gleichung 10: L ‚ hopitals Regel zweimal Frage pt.,4 - Schritt 4:
Unendlichkeit ist keine unbestimmte Form, also sind wir fertig und die Antwort lautet ∞\infty∞