aproximación lineal
digamos que un día olvidaste una calculadora y realmente quieres encontrar cómo es la raíz cuadrada de 2. ¿Cómo lo averiguaríamos sin una calculadora? ¡Podemos usar aproximación lineal!
linealización de una función
la linealización de una función se trata de encontrar la línea tangente de la función en un punto específico de una manera diferente., La linealización de la fórmula es la siguiente:

donde L(x) es la ecuación de la recta tangente en el punto a.
¿Cómo es esto útil para nosotros? Bueno, realmente podemos usar esta ecuación para aproximar valores de la función cerca del punto A. echa un vistazo a este gráfico.,
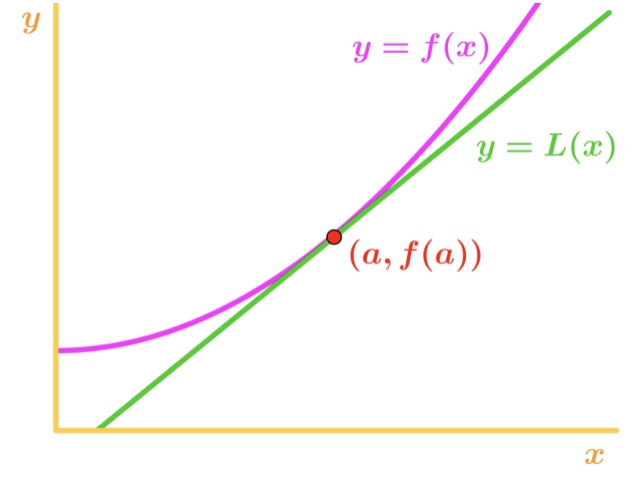
observe que para los valores de x cerca del punto a, vemos que la función y la línea tangente relativamente cerca uno del otro. Debido a esto, podemos escribir que la función es aproximadamente igual a la recta tangente cerca del punto a., En otras palabras,

donde ≈\aprox≈ es aproximadamente el símbolo. Esta ecuación se conoce como la fórmula de aproximación lineal. Es lineal en un sentido que la tangente es una línea recta y la estamos usando para aproximar la función. Usando esta aproximación, podemos aproximar valores que no se pueden hacer a mano. Por ejemplo,la raíz cuadrada de 2 o el logaritmo natural de 5 se puede aproximar!, Una cosa importante a tener en cuenta es que esta aproximación solo funciona para valores de x cerca del punto a. si tienes un valor de x lejos del punto a, entonces la aproximación se vuelve realmente inexacta.
Ahora no echemos un vistazo a algunos ejemplos de encontrar la linealización de una función y luego ver cómo utilizar la aproximación lineal!
Encuentre la linealización L(x) de la función en un
Pregunta 1: Considere la función
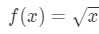
supongamos que queremos encontrar la linealización de la función en el punto a=4.
para encontrar la linealización L(x), recuerde que

- Paso 1: encuentra a
- Paso 2: Encuentra f(A)
- Paso 3: Encuentra f'(a).
- Paso 4: Conecte los tres en la fórmula para encontrar L (x)
-
¡sigamos estos pasos!,
Paso 1: afortunadamente a = 4 se nos da en la pregunta, por lo que no tenemos que buscarlo.
- Paso 2:
Observe que
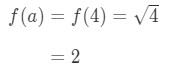
la Ecuación 1: Linealización pregunta pt. 3 - Paso 3:
Saber que la derivada de la raíz cuadrada es
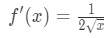
la Ecuación 1: Linealización pregunta pt., 4 And so plugging in x=a gives us:
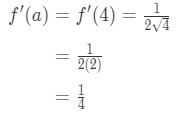
Equation 1: Linearization question pt. 5 - Step 4:
Since we know a, f(a), and f'(a), we can now plug it into L(x) to find the linearization of f(x).
Hence,
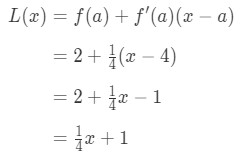
Equation 1: Linearization question pt., 6 So L(x)=14\frac{1}{4}41x+1 es la linealización de esta función en el punto x=4. Además, también es la línea tangente de la función en el punto x = 4.
cómo hacer la aproximación lineal
recuerde que antes dijimos que podríamos usar la ecuación de la recta tangente para aproximar los valores de la función cerca de a? Intentemos esto con la linealización que encontramos antes. Recordar que
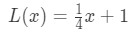
para puntos cercanos a x=4. Podemos cambiar esto en una aproximación lineal para f (x) diciendo que:
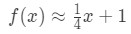
Ahora, digamos que quiero aproximar f(4.04). Si tuvieras que conectar esto a la función original, entonces obtendrías 4.04\sqrt{4.04}4.04 . Esto sería muy difícil de calcular sin una calculadora., Sin embargo, usando aproximación lineal, podemos decir que

hasta ahora, estas preguntas nos dieron una función y un punto para trabajar. ¿Y si no se les dio nada de esto? ¿Qué pasa si la pregunta solo nos dice que estimemos un número?
Use aproximación lineal para estimar un número
supongamos que queremos estimar 10\sqrt{10} 10. ¿Cómo lo haríamos?, Necesitaríamos utilizar la aproximación lineal

pero ni siquiera tenemos una función y un punto para trabajar. Esto significa que tenemos que hacerlos nosotros mismos. Esto nos lleva a hacer los siguientes pasos:
- Paso 1: Crear una función
- Paso 2: Crear punto a
- Paso 3: Encontrar f(A) y f'(A)
- Paso 4: Conecte todo en la fórmula de aproximación lineal
¡sigamos los pasos!,
Pregunta 2: estimación 10\sqrt{10} 10
- Paso 1: vamos a llegar a una función. Tenga en cuenta que estamos estimando
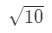
la Ecuación 3: Estimación lineal aprox. pt.2 necesitamos de alguna manera hacer una relación entre f(x) y 10\sqrt{10}10. No podemos decir que f ( x) = 10\sqrt{10}10 porque la función no será dependiente de x. entonces, ¿por qué no hacemos esto? Vamos
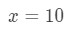
la Ecuación 3: Estimación lineal aprox. pt.,3 Si hacemos eso, entonces estamos diciendo básicamente
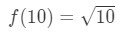
la Ecuación 3: Estimación lineal aprox. pt.4 ahora obviamente podemos decir cuál debe ser la función. Vamos
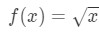
la Ecuación 3: Estimación lineal aprox. pt.5 Así que tenemos una función, pero ahora necesitamos un punto a trabajar.,
- Paso 2:
la clave para encontrar el valor a correcto es considerar dos cosas:
1) Asegúrese de que el valor a esté cerca de x
2) Asegúrese de que f(a) sea un buen número.
¿a = 8 sería suficiente? Bueno, 8 es bastante cerca de 10 por lo que no está mal. Sin embargo,
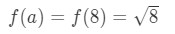
la Ecuación 3: Estimación lineal aprox. pt.6 Observe que 8\sqrt{8}8 no es un número muy agradable. De hecho, obtienes un montón de números decimales. Así que tenemos que intentar otra cosa.,
¿a = 9 sería suficiente? Una vez más, 9 es bastante cerca de 10 por lo que está bien. También,

la Ecuación 3: Estimación lineal aprox. pt.7 f(a) es en realidad un buen número entero aquí, así que esto realmente funciona! Así que elegir a = 9 es suficiente.
- Paso 3:
tenga en cuenta que a partir de principios:

la Ecuación 3: Estimación lineal aprox. pt.,8 Calculating f'(x) we have again:

Equation 3: Estimate with linear approx. pt.9 So
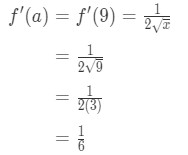
Equation 3: Estimate with linear approx. pt.,10 - Step 4:
Going back to the linear approximation formula we have:

Equation 3: Estimate with linear approx. pt.11 Plugging a, f(a), f'(a), f(x), and x in our formula you will see that:

Equation 3: Estimate with linear approx. pt.12 Hence, we just approximated the number!,
si desea más problemas de práctica sobre aproximación lineal, entonces le recomiendo que mire este enlace aquí.
http://tutorial.math.lamar.edu/Classes/CalcI/LinearApproximations.aspx
sobreestimar y subestimar
sabemos que la aproximación lineal es solo una estimación del valor de la función en un punto especificado. Sin embargo, ¿cómo sabemos que si nuestra estimación es una sobreestimación o una subestimación? Calculamos la segunda derivada y miramos la concavidad.,
Cóncavo arriba vs Cóncavo abajo
si la segunda derivada de la función es mayor que 0 para valores cercanos a a, entonces la función es cóncava arriba. Esto significa que nuestra aproximación será una subestimación. En otras palabras,
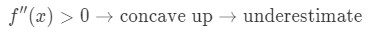
¿por Qué? Echemos un vistazo a este gráfico.,
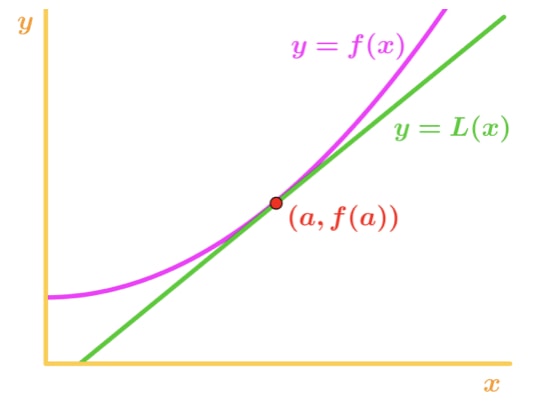
Observe que f(x) es cóncava hacia arriba y la línea tangente se encuentra justo debajo de f(x). Digamos que usamos la recta tangente para aproximar f (x). Entonces los valores y de la línea tangente siempre van a ser menores que el valor real de f (x). Por lo tanto, tenemos una subestimación
ahora si la segunda derivada de la función es menor que 0 para valores cerca de a, entonces la función es cóncava hacia abajo., Esto significa que nuestra aproximación será una sobreestimación. En otras palabras,
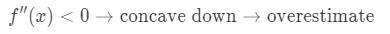
de Nuevo, ¿por qué? Echemos un vistazo a otro gráfico.
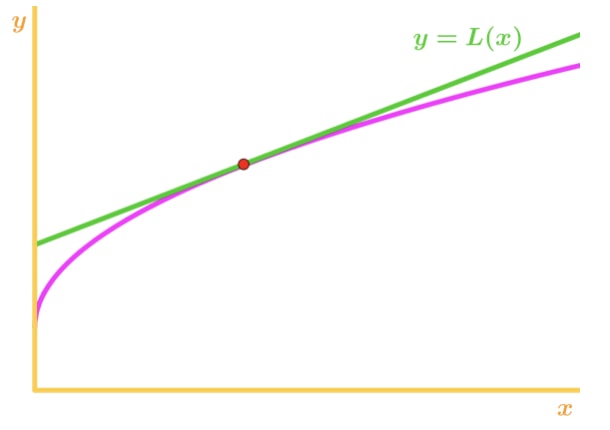
Observe que f(x) es cóncava hacia abajo y la línea tangente está justo encima de f(x). Una vez más, digamos que vamos a usar la recta tangente para aproximar f(x)., Entonces los valores y de la recta tangente siempre van a ser mayores que el valor real de f (x). Por lo tanto, tenemos una sobreestimación.
así que si alguna vez necesitas ver si tu valor es una subestimación o una sobreestimación, asegúrate de seguir estos pasos:
- Paso 1: Encuentra la segunda derivada
- Paso 2: Mira la concavidad de la función cerca del punto a
- Paso 3: confirma que es una subestimación/sobreestimación
echemos un vistazo a un ejemplo:
pregunta 3: x) = x\sqrt{x}x y a = 4. Si nos lineal aproximada f (4.,04), ¿sería una sobreestimación o una subestimación?
- Paso 1: vea que
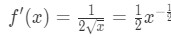
ecuación 4: sobreestimar la pregunta pt.1 Así que la segunda derivada es
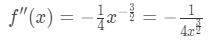
la Ecuación (4): Sobreestimar pregunta pt.2 - Paso 2:
observe que a = 4, por lo que queremos ver valores positivos de x cerca de 4. Ahora mira la segunda derivada., Cuando x es positivo, vemos que
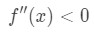
la Ecuación (4): Sobreestimar pregunta pt.3 por lo tanto, es cóncava hacia abajo
- Paso 3:
sabemos que si la función es cóncava hacia abajo, entonces la línea tangente estará por encima de la función. Por lo tanto, el uso de la línea tangente como una aproximación dará un valor sobreestimado.
diferenciales
no solo podemos aproximar valores con aproximación lineal, sino que también podemos aproximar con diferenciales., Para aproximar, utilizamos la siguiente fórmula
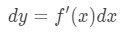
donde dy y dx son diferenciales, y f'(x) es la derivada de F en términos de x. dado que estamos tratando con cambios muy pequeños en X E y, entonces vamos a utilizar el hecho de que:
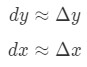
Sin embargo, la mayoría de las preguntas que hacemos implican establecer
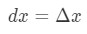
así que el uso de estos hechos nos llevará a tener:
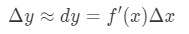
Esta aproximación es muy útil cuando se aproxima el cambio de y., Tenga en cuenta que en ese entonces no tenían Calculadoras, por lo que esta es la mejor aproximación que podrían obtener para funciones con raíces cuadradas o registros naturales.
La mayor parte del tiempo tendrá que buscar F'(x) y Δ\Deltaδx usted mismo. En otras palabras, siga estos pasos para aproximar Δ\DeltaΔy!
- Paso 1: Encuentra Δ\DeltaΔx
- Paso 2: Encuentra f'(x)
- Paso 3: Conecta todo en la fórmula para encontrar dy. dy será la aproximación Para Δ\DeltaΔy.
veamos un ejemplo de uso de esta aproximación:
Pregunta 4: considere la función y = ln (x + 1)., Supongamos que X cambia de 0 a 0.01. Δ \ Deltaδy Aproximado.
- Paso 1: Observe que X cambia de 0 a 0.01, por lo que el cambio en x sería:
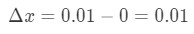
ecuación 6: pregunta diferencial pt.1 - Paso 2:
La derivada sería:
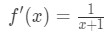
Ecuación 6: Diferencial pregunta pt.,2 - Paso 3:
Conectar todo en tenemos:
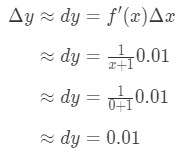
Ecuación 6: Diferencial pregunta pt.3 por lo tanto, Δ\Deltaδy ≈\approx≈ 0.01
Sin embargo, la mayoría de las veces queremos estimar un valor de la función, y no el cambio del valor. Por lo tanto, agregaremos ambos lados de la ecuación por y, lo que nos da:
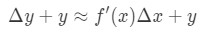
que es la misma como:
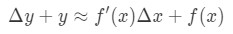
Esta ecuación es un poco difícil de leer, así que vamos a reorganizar aún más. Vamos a tratar de deshacerse de Y y Δ\DeltaΔy. Observe que Δ\deltaδy+y es básicamente lo mismo que encontrar el valor de la función en Δ\Deltaδx + x. En otras palabras,
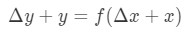
por lo tanto sustituyendo esto en nuestra aproximación anterior nos dará:
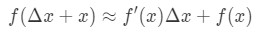
donde f(Δ\Deltaδx+x) es el valor que estamos tratando de estimar. ¿Cómo usamos esta fórmula? Recomiendo seguir estos pasos:
usemos estos pasos para la siguiente pregunta.
Pregunta 5: Use diferenciales para aproximarse a 10\sqrt{10} 10.
- Paso 1: Compare f(Δ\Deltaδx+x) con 10\sqrt{10}10., Since 10\sqrt{10}10 has a square root and 9 is a perfect square that is closest to 10, then let
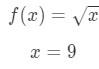
Equation 7: Approximate value with differentials pt.1 Notice that:
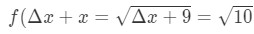
Equation 7: Approximate value with differentials pt.,2 Ver que no hay otra opción sino para que Δ\DeltaΔx = 1
- Paso 2:
Ver que la derivada se obtiene:

Ecuación 7: valor Aproximado con diferenciales de pt.3 por Lo que esto implica
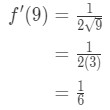
Ecuación 7: valor Aproximado con diferenciales de pt.,4 - Paso 3:
Conectar todo en la fórmula nos da:
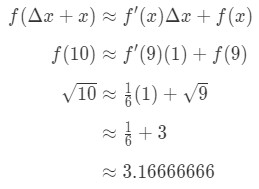
Ecuación 7: valor Aproximado con diferenciales de pt.5 por lo tanto, solo aproximamos el número.
una cosa interesante a tener en cuenta es que tanto la aproximación lineal como los diferenciales dan el mismo resultado para 10\sqrt{10}10.,
si quieres saber más sobre diferenciales, haz clic en este enlace:
http://tutorial.math.lamar.edu/Classes/CalcI/LinearApproximations.aspx
probando la regla de L’hospital usando aproximación lineal
ahora hemos aprendido mucho sobre aproximación lineal, pero ¿qué más podemos hacer con ella? Realmente podemos utilizar la fórmula de aproximación lineal para probar una regla conocida como regla de L’Hospital . Así es como funciona la prueba.
recuerde que la fórmula de aproximación lineal es:

a Ver que podemos reorganizar la fórmula, de modo que:
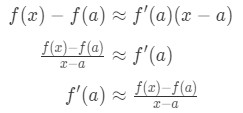
darse cuenta de que la aproximación se vuelve más y más precisa a medida que elegimos valores de x que están más cerca de a. En otras palabras, si tomamos el límite como x→A, entonces serán iguales. So
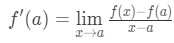
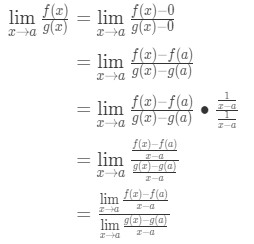
ahora observe que podemos aplicar la fórmula que derivamos anteriormente aquí. Así que ahora
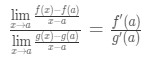
ahora en lugar de escribir f'(A) y g'(A), podemos aplicar límites como x→a (porque sabemos que f y g son diferenciables)., So
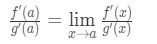
por lo tanto, hemos demostrado que:
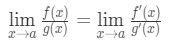
que es L’Hospital de la Regla .
cuándo usar la regla de l’Hopital
siempre queremos aplicar la regla de l’hoptial cuando nos encontramos con límites indeterminados. Hay dos tipos de formas indeterminadas., Estos indeterminado formas sería:
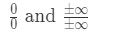
muchas personas cometen el error de usar la regla de l’hospital, sin siquiera comprobar si se trata de un límite indeterminado. ¡Así que asegúrate de comprobarlo primero! De lo contrario, no funcionará y obtendrá la respuesta incorrecta. Aquí hay una guía para usar la regla de l’Hopital:
- Paso 1: evaluar el límite directamente.
- Paso 2: Compruebe si es una de las formas indeterminadas. Si lo es, vaya al paso 3.,
- Paso 3: Utilice la regla de l’Hopital.
- Paso 4: Compruebe si obtiene otro formulario indeterminado. Repita el paso 3 si lo hace.
echemos un vistazo a algunos ejemplos usando estos pasos.
la Pregunta 6: Evaluar el límite
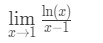
- Paso 1: Evaluar el límite directamente nos da
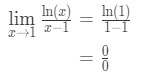
Ecuación 9: L’hospital de la regla pregunta pt.,2 - Paso 2:
Sí, es una de las formas indeterminadas.
- Paso 3:
Aplicar la regla de l’hospital, tenemos:
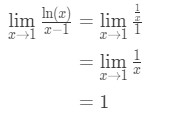
Ecuación 9: L’hospital de la regla pregunta pt.3 - Paso 4:
uno no es una forma indeterminada, así que hemos terminado y la respuesta es 1.
ahora esa pregunta fue un poco fácil, así que por qué no echamos un vistazo a algo que es un poco más difícil.,
Pregunta 7: evaluar el límite
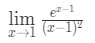
- Paso 1: Evaluar el límite directamente vemos que:
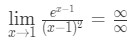
Ecuación 10: L’hospital de la regla dos veces la pregunta pt.2 - Paso 2:
Esta es una forma indeterminada, así que vaya al paso 3.,
- Paso 3:
aplicando la regla de l’Hopital tenemos
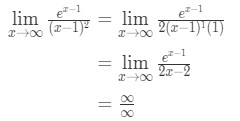
ecuación 10: La regla de L’Hopital pregunta dos veces pt.3 - Paso 4:
Esta es otra forma indeterminada. Así que tenemos que volver al paso 3 y aplicar las reglas de l’hoptial de nuevo.
- Paso 3:
aplicando la regla de l’Hopital nuevamente tenemos:
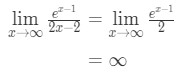
ecuación 10: La regla de L’Hopital pregunta dos veces pt.,4 - Paso 4:
Infinity no es una forma indeterminada, así que hemos terminado y la respuesta es ∞\infty∞