aproximação Linear
digamos que um dia se esqueceu de uma calculadora e deseja realmente descobrir como é a raiz quadrada de 2. Como descobriríamos sem uma calculadora? Podemos usar aproximação linear!
Linearização de uma função
A linearização de uma função é apenas sobre encontrar a linha tangente da função em um ponto específico de uma maneira diferente., A linearização fórmula é a seguinte:

onde L(x) é a equação da reta tangente no ponto a.
Como é que isto é útil para nós? Bem, nós podemos realmente usar esta equação para aproximar os valores da função perto do ponto A. Dê uma olhada neste gráfico. ,
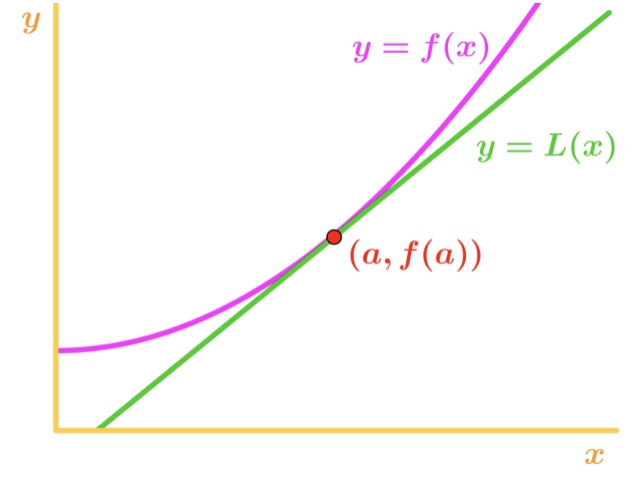
Observe que para valores de x perto de ponto, vemos que a função e a reta tangente é relativamente próximos uns dos outros. Por causa disso, somos capazes de escrever que a função é aproximadamente igual à linha tangente perto do ponto A., Em outras palavras,

onde ≈\approx≈ está a cerca de símbolo. Esta equação é conhecida como a fórmula de aproximação linear. É linear em um sentido que a tangente é uma linha reta e nós estamos usando-a para aproximar a função. Usando esta aproximação, somos capazes de aproximar valores que não podem ser feitos à mão. Por exemplo, a raiz quadrada de 2 ou o log natural de 5 podem ser todos aproximados!, Uma coisa importante a notar é que esta aproximação só funciona para os valores x perto do ponto A. Se você tem um valor x longe do ponto a, então a aproximação torna-se realmente imprecisa.
Agora não vamos dar uma olhada em alguns exemplos de encontrar a linearização de uma função e, em seguida, olhar para como usar a aproximação linear!
Find the linearization of L(x) of the function at a
Question 1: Consider the function
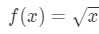
digamos que queremos encontrar a linearização da função no ponto a=4.
Para encontrar a linearização L(x), lembre-se que

- Step 1: Find a
- Step 2: Find f(A)
- Step 3: Find f'(a).
- Passo 4: Plug all three into the formula to find L (x)
-
Let’s follow these steps!,
Passo 1: felizmente a = 4 nos é dado na pergunta, então não temos que procurá-lo.
- Step 2:
Notice that
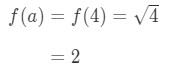
Equation 1: Linearization question pt. 3 - Passo 3:
Sabe-se que a derivada de raízes quadradas é
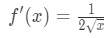
Equação 1: Linearização pergunta pt., 4 And so plugging in x=a gives us:
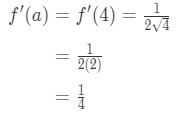
Equation 1: Linearization question pt. 5 - Step 4:
Since we know a, f(a), and f'(a), we can now plug it into L(x) to find the linearization of f(x).
Hence,
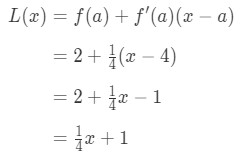
Equation 1: Linearization question pt., 6 Então L(x)=14\frac{1}{4}41x+1 é a linearização desta função no ponto x=4. Além disso, é também a linha tangente da função no ponto x=4.
Como fazer a aproximação linear
Lembra-te antes que dissemos que podíamos usar a equação da linha tangente para aproximar os valores da função perto de a? Vamos tentar com a linearização que encontramos antes. Recordar que
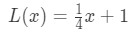
para pontos próximos de x=4. Podemos mudar isso para uma aproximação linear para f (x) dizendo que:
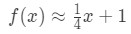
agora, digamos que eu quero aproximar f(4.04). Se ligasse isto à função original, receberia 4,04\sqrt{4,04}4,04 . Isto seria muito difícil de calcular sem uma calculadora., No entanto, a utilização de aproximação linear, pode-se dizer que

até agora, estas questões nos deram uma função e um ponto para trabalhar. E se nada disto foi dado? E se a pergunta nos diz apenas para estimar um número?
Use aproximação Linear para estimar um número
suponha que queremos estimar 10\sqrt{10}10. Como o faríamos?, Seria necessário usar a aproximação linear

mas nós nem sequer temos uma função e um ponto para trabalhar. Isto significa que temos de ser nós a fazê-los. Isto leva-nos a fazer os seguintes passos:
- Passo 1: criar uma função
- Passo 2: criar um ponto a
- Passo 3: Encontrar f(A) E f'(A)
- Passo 4: Ligar tudo à fórmula de aproximação linear
vamos seguir os passos!,
Pergunta 2: estimativa 10\sqrt{10}10
- Passo 1: vamos criar uma função. Note that we are estimating
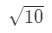
Equation 3: Estimate with linear approx. tamanho.2 precisamos, de alguma forma, fazer uma relação entre f(x) e 10\sqrt{10}10. Não podemos dizer que f ( x) = 10\sqrt{10}10 porque a função não será dependente de x. Então por que não fazemos isso? Let
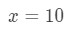
Equation 3: Estimate with linear approx. tamanho.,3 Se fizermos isso, estamos basicamente dizendo
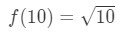
Equação 3: Estimativa linear com aprox. tamanho.4 podemos agora obviamente dizer qual a função deve ser. Let
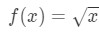
Equation 3: Estimate with linear approx. tamanho.5 assim temos uma função, mas agora precisamos de um ponto a para trabalhar.,
- Passo 2:
a chave para encontrar o valor certo a é considerando duas coisas:
1) Certifique-se de que o valor a está próximo de x
2) Certifique-se de que f(A) é um número agradável.a = 8 seria suficiente? Bem, 8 é quase 10, por isso não é mau. No entanto,
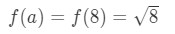
Equação 3: Estimativa linear com aprox. tamanho.6 Notice that 8\sqrt{8}8 is not a very nice number. Na verdade, recebes um monte de números decimais. Temos de tentar outra coisa.,a = 9 seria suficiente? Mais uma vez, o 9 é quase 10, por isso está tudo bem. Also,

Equation 3: Estimate with linear approx. tamanho.7 f(A) é realmente um bom número inteiro aqui, então isso realmente funciona! Então escolher a = 9 é suficiente.
- Passo 3:
Note que a partir de anterior:

Equação 3: Estimativa linear com aprox. tamanho.,8 Calculating f'(x) we have again:

Equation 3: Estimate with linear approx. pt.9 So
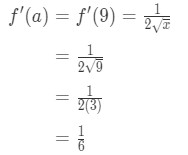
Equation 3: Estimate with linear approx. pt.,10 - Step 4:
Going back to the linear approximation formula we have:

Equation 3: Estimate with linear approx. pt.11 Plugging a, f(a), f'(a), f(x), and x in our formula you will see that:

Equation 3: Estimate with linear approx. pt.12 Hence, we just approximated the number!,
Se você quiser mais problemas de prática sobre aproximação linear, então eu recomendo que você olhe para esta ligação aqui.
http://tutorial.math.lamar.edu/Classes/CalcI/LinearApproximations.aspx
Superestimar e Subestimar
sabemos que a aproximação linear é apenas uma estimativa do valor da função em um determinado ponto. No entanto, como é que sabemos se a nossa estimativa é uma sobrestimação ou uma subavaliação? Calculamos a segunda derivada e olhamos para a concavidade.,
côncavo para cima vs côncavo para baixo
Se a segunda derivada da função é maior que 0 para valores próximos a, então a função é côncava para cima. Isto significa que a nossa aproximação será uma subestimação. Em outras palavras,
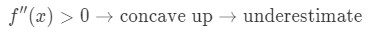
Por quê? Vamos dar uma olhada neste gráfico.,
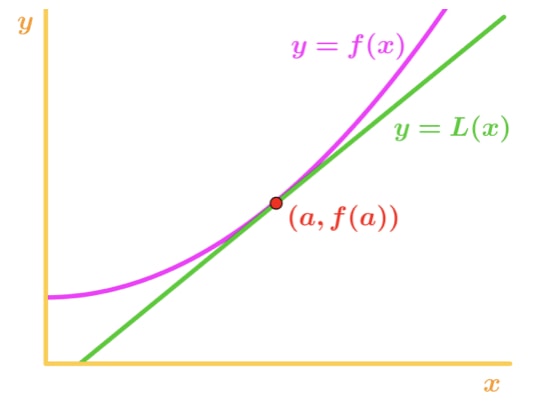
Observe que f(x) é côncava para cima e a reta tangente é direito f(x). Digamos que devemos usar a linha tangente para aproximar f (x). Então os valores y da linha tangente serão sempre menores que o valor real de f(x). Portanto, temos uma subestimação
agora se a segunda derivada da função é menor que 0 para valores próximos a, então a função é côncava para baixo., Isto significa que a nossa aproximação será uma sobrestimação. Em outras palavras,
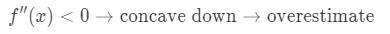
de Novo, por quê? Vamos ver outro gráfico.
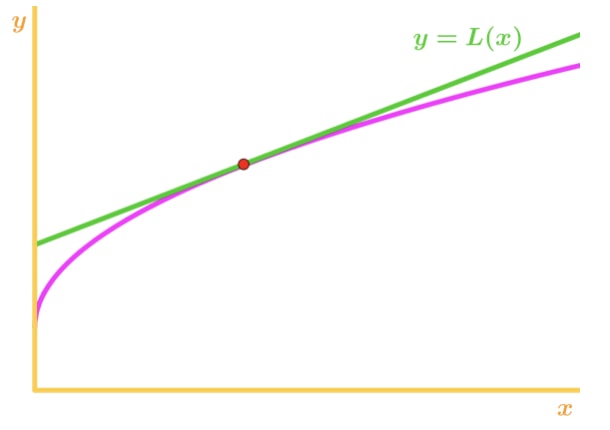
Observe que f(x) é côncava para baixo e a reta tangente é direito acima de f(x). Mais uma vez, digamos que vamos usar a linha tangente para aproximar f(x)., Então os valores y da linha tangente serão sempre maiores que o valor real de f(x). Por isso, temos uma sobrestimação.
por Isso, se você precisa ver se o seu valor é uma subestimação ou superestimação, certifique-se de que você siga estas etapas:
- Passo 1: Encontrar a segunda derivada
- Passo 2: observe a concavidade da função de perto de ponto de um
- Passo 3: Confirmar que ele está subestimado/superestimar
Vamos dar uma olhada em um exemplo:
a Pergunta 3: seja f(x) = x\sqrt{x}x e a = 4. Se nós lineares aproximarmos f (4.,04), seria uma sobrestimação ou uma subestimação?
- Step 1: See that
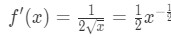
Equation 4: Overestimate question pt.1 Então a segunda derivada é
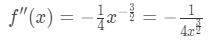
Equação 4: Superestimar pergunta pt.2 - Step 2:
Notice that a=4, so we want to look at positive values of x near 4. Agora Veja o segundo derivado., When x is positive, we see that
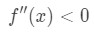
Equation 4: Overestimate question pt.3 por isso, é côncava para baixo
- Passo 3:
sabemos que, se a função é côncava para baixo, então a reta tangente será acima da função. Assim, usar a linha tangente como uma aproximação dará um valor sobrestimado.
diferenciais
não só podemos aproximar valores com aproximação linear, como também podemos aproximar-nos com diferenciais., Para aproximar, usamos a seguinte fórmula
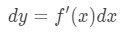
onde dy e dx são diferenciais, e f'(x) é a derivada de f em relação a x. Uma vez que estamos lidando com pequenas mudanças em x e y, então vamos usar o fato de que:
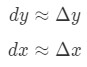
no Entanto, a maioria das questões que envolvem a definição
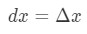
Então, usando estes fatos nos leva a ter:
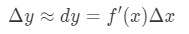
esta aproximação é muito útil quando se aproxima a mudança de y., Tenha em mente então eles não tinham Calculadoras, então esta é a melhor aproximação que eles poderiam obter para funções com raízes quadradas ou logs naturais.
na maioria das vezes você terá que procurar por f'(x) e Δ\DeltaΔx você mesmo. Em outras palavras, siga estes passos para aproximar Δ\DeltaΔy!
- Step 1: Find Δ\DeltaΔx
- Step 2: Find f'(x)
- Step 3: Plug everything into the formula to find dy. dy será a aproximação Para Δ\DeltaΔy.
Let’s look at an example of using this approximation:
Question 4: Consider the function y = ln(x + 1)., Suponha que x muda de 0 para 0,01. Aproximadamente Δ\DeltaΔy.
- Step 1: Notice that x changes from 0 to 0,01, so the change in x would be:
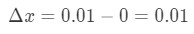
Equation 6: Differential question pt.1 - Passo 2:
A derivada seria:
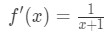
Equação 6: Diferencial pergunta pt.,2 - Passo 3:
Ligar tudo em nós tem:
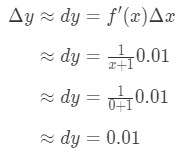
Equação 6: Diferencial pergunta pt.3 Portanto, Δ\DeltaΔy ≈\approx≈ 0.01
no Entanto, a maior parte do tempo queremos estimar um valor da função, e não a alteração do valor. Assim, adicionaremos ambos os lados da equação por y, que nos dá:
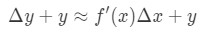
o que é o mesmo que:
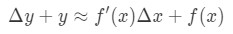
esta equação é um pouco difícil de ler, por isso vamos reorganizá-la ainda mais. Vamos tentar livrar-nos do y E Do Δ\DeltaΔy. Observe que Δ\DeltaΔy+ y é basicamente o mesmo que encontrar o valor da funł c ao Δ\DeltaΔx+x. Em outras palavras,
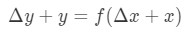
Portanto, substituindo na nossa aproximação acima nos dará:
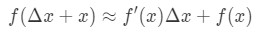
where f(Δ\DeltaΔx+x) is value we are trying to estimate. Como usamos esta fórmula? Eu recomendo seguir estes passos:
vamos usar estes passos para a seguinte pergunta.Pergunta 5: usar diferenciais para aproximadamente 10\sqrt{10}10.
- Passo 1: comparar f (Δ \ DeltaΔx+x)com 10\sqrt{10}10., Since 10\sqrt{10}10 has a square root and 9 is a perfect square that is closest to 10, then let
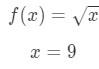
Equation 7: Approximate value with differentials pt.1 Notice that:
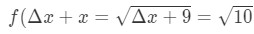
Equation 7: Approximate value with differentials pt.,2 Veja que não há nenhuma escolha mas para deixar o Δ\DeltaΔx = 1
- Passo 2:
Veja que o derivativo dá a:

Equação 7: valor Aproximado com diferenciais pt.3 isto implica
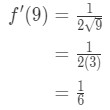
Equação 7: valor Aproximado com diferenciais pt.,4 - Passo 3:
Ligar tudo na fórmula dá-nos a:
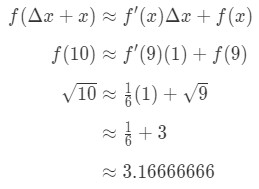
Equação 7: valor Aproximado com diferenciais pt.5 portanto, nós apenas aproximamos o número.
uma coisa interessante a notar é que a aproximação linear e os diferenciais ambos dão o mesmo resultado para 10\sqrt{10}10.,
Se você deseja saber mais sobre os diferenciais, clique neste link:
http://tutorial.math.lamar.edu/Classes/CalcI/LinearApproximations.aspx
Provando a Regra de L’Hospital usando aproximação linear
Agora temos aprendido muito sobre a aproximação linear, mas o que mais podemos fazer com ele? Podemos usar a fórmula de aproximação linear para provar uma regra conhecida como Regra do Hospital . Aqui está como a prova funciona.
Recall that the linear approximation formula is:

Veja o que podemos reorganizar a fórmula de modo que:
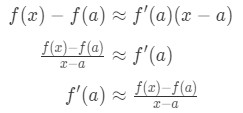
Perceber que a aproximação torna-se mais e mais precisos como nós escolhemos os valores de x que estão mais perto de um. Em outras palavras, se tomarmos o limite como x→a, então eles serão iguais. So
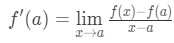
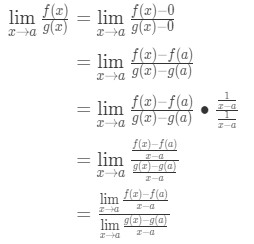
agora note que podemos aplicar a fórmula que derivamos anteriormente aqui. So now
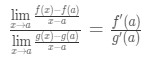
Agora, em vez de escrever f'(a) e g'(a), podemos aplicar limites x→a (porque sabemos que f e g são diferenciáveis)., So
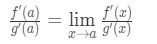
por isso, acabamos de mostrar que:
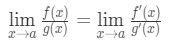
qual é a Regra de L’Hospital .
quando usar a regra de l’Opital
sempre queremos aplicar a regra de l’optial quando encontramos limites indeterminados. Existem dois tipos de formas indeterminadas., Estes indeterminado a forma:
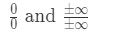
muitas pessoas cometem o erro de usar a regra de l’hopital, sem mesmo verificar se ele é indeterminado limite. Por isso certifica-te que o verificas primeiro! Caso contrário, não funcionará e obtereis a resposta errada. Aqui está um guia para usar a regra de l’Opital:
- Passo 1: avaliar o limite diretamente.
- Passo 2: Verifique se é uma das formas indeterminadas. Se for, vá para o Passo 3.,Passo 3: usar a regra de l’Opital.
- Passo 4: Verifique se tem outra forma indeterminada. Repita o Passo 3 se o fizer.
vamos dar uma olhada em alguns exemplos usando estes passos.Pergunta 6: avalie o limite
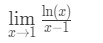
- Passo 1: Avaliar o limite diretamente nos dá
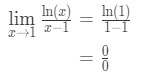
Equação 9: L’hopital da regra pergunta pt.,2 - Passo 2:
Sim, é uma das formas indeterminadas.
- Passo 3:
Aplicando a regra de l’hopital, temos:
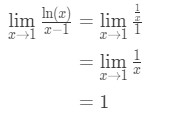
Equação 9: L’hopital da regra pergunta pt.3 - Passo 4:
one is not an indeterminate form, so we are done and the answer is 1.
Agora que a questão foi um pouco fácil, então por que não damos uma olhada em algo que é um pouco mais difícil.,Pergunta 7: avaliar o limite
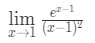
- Passo 1: Avaliar o limite diretamente, podemos ver que:
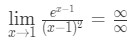
Equação 10: L’hopital da regra duas vezes pergunta pt.2 - Step 2:
This is an indeterminate form, so go to step 3.,
- Passo 3:
Aplicando a regra de l’hopital, temos
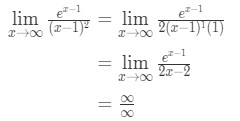
Equação 10: L’hopital da regra duas vezes pergunta pt.3 - Passo 4:
esta é outra forma indeterminada. Temos de voltar ao passo 3 e aplicar as regras do aeroporto.
- Passo 3:
Aplicando a regra de l’hopital, novamente, temos:
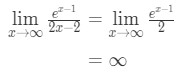
Equação 10: L’hopital da regra duas vezes pergunta pt.,4 - Passo 4:
o Infinito não é indeterminado forma, então, estamos a fazer e a resposta é: ∞\infty∞