lineaire benadering
laten we zeggen dat je op een dag een rekenmachine bent vergeten en je echt wilt weten hoe wat de vierkantswortel van 2 is. Hoe komen we daar achter zonder rekenmachine? We kunnen lineaire benadering gebruiken!
linearisatie van een functie
De linearisatie van een functie gaat over het vinden van de raaklijn van de functie op een specifiek punt op een andere manier., De linearisatieformule is:

waarbij L(x) de vergelijking is van de raaklijn op punt a.
Hoe is dit nuttig voor ons? We kunnen deze vergelijking gebruiken om de waarden van de functie bij punt a te benaderen.,
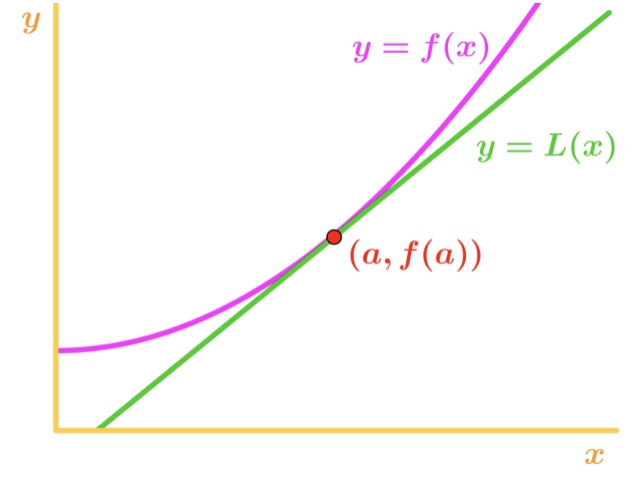
merk op dat Voor x-waarden in de buurt van punt a, we zien dat de functie en de raaklijn relatief dicht bij elkaar liggen. Hierdoor kunnen we schrijven dat de functie ongeveer gelijk is aan de raaklijn bij punt a., Met andere woorden,

waarbij ≈\approx≈ het ongeveer-symbool is. Deze vergelijking staat bekend als de lineaire benaderingsformule. Het is lineair in de zin dat de raaklijn een rechte lijn is en we gebruiken het om de functie te benaderen. Met behulp van deze benadering zijn we in staat om waarden te benaderen die niet met de hand kunnen worden gedaan. Bijvoorbeeld, de vierkantswortel van 2 of de natuurlijke log van 5 kunnen allemaal worden benaderd!, Een belangrijk ding om op te merken is dat deze benadering alleen werkt voor x-waarden in de buurt van punt A. als je een X-waarde ver van punt a hebt, dan wordt de benadering echt onnauwkeurig.
kijken we nu niet naar een paar voorbeelden van het vinden van de linearisatie van een functie en dan kijken we naar hoe lineaire benadering te gebruiken!
vind de linearisatie van L (x) van de functie bij een
Vraag 1: overweeg de functie
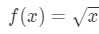
laten we zeggen dat we de linearisatie van de functie willen vinden op punt A=4.
om de linearisatie L(x) te vinden, bedenk dan dat

- Stap 1: Zoek een
- Stap 2: Zoek f(a)
- Stap 3: Zoek f'(a).
- Stap 4: Plug alle drie in de formule om L(x)
-
te vinden laten we deze stappen volgen!,
Stap 1: gelukkig wordt A = 4 gegeven in de vraag, dus we hoeven er niet naar te zoeken.
- Stap 2:
merk op dat
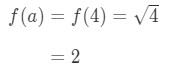
vergelijking 1: Linearisatievraag pt. 3 - Stap 3:
weet dat de afgeleide van vierkantswortels
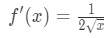
vergelijking 1: Linearisatievraag pt., 4 And so plugging in x=a gives us:
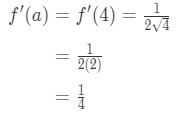
Equation 1: Linearization question pt. 5 - Step 4:
Since we know a, f(a), and f'(a), we can now plug it into L(x) to find the linearization of f(x).
Hence,
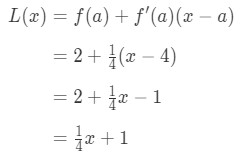
Equation 1: Linearization question pt., 6 dus L(x)=14\frac{1}{4}41x+1 is de linearisatie van deze functie op punt x=4. Daarnaast is het ook de raaklijn van de functie op punt x = 4.
hoe doe je een lineaire benadering
herinner je dat we eerder zeiden dat we de vergelijking van de raaklijn konden gebruiken om waarden van de functie in de buurt van a te benaderen? Laten we dit proberen met de linearisatie die we eerder vonden. Bedenk dat
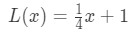
voor punten in de buurt van x=4. We kunnen dit veranderen in een lineaire benadering voor f(x) door te zeggen dat:
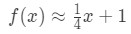
laten we nu zeggen dat ik f(4.04) wil benaderen. Als je dit in de oorspronkelijke functie zou steken, dan zou je 4.04\sqrt{4.04}4.04 krijgen . Dit zou echt moeilijk te berekenen zijn zonder een rekenmachine., Echter, met behulp van lineaire benadering, kunnen we zeggen dat

tot nu toe gaven deze vragen ons een functie en een punt om mee te werken. Wat als er helemaal geen van deze zijn gegeven? Wat als de vraag ons alleen vertelt om een getal te schatten?
gebruik lineaire benadering om een getal
te schatten stel dat we 10\sqrt{10}10 willen schatten. Hoe zouden we het doen?, We zouden de lineaire benadering moeten gebruiken

maar we hebben niet eens een functie en een punt om mee te werken. Dit betekent dat we ze zelf moeten maken. Dit leidt ons tot de volgende stappen:
- Stap 1: Maak een functie
- Stap 2: Maak punt A
- Stap 3: Zoek f (a) en f ‘ (a)
- Stap 4: Sluit alles aan op de lineaire benaderingsformule
laten we de stappen volgen!,
vraag 2: schatting 10 \ sqrt{10}10
- Stap 1: Laten we een functie bedenken. Merk op dat we
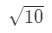
vergelijking 3: schatting met lineaire CA. pt.2 we moeten op de een of andere manier een relatie maken tussen f(x) en 10\sqrt{10}10. We kunnen niet zeggen dat f ( x) = 10 \ sqrt{10}10 omdat de functie niet afhankelijk zal zijn van x. Laat
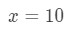
vergelijking 3: schatting met lineaire CA. pt.,3 Als we dat doen, dan zeggen we eigenlijk
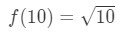
vergelijking 3: schatting met lineaire CA. pt.4 we kunnen nu duidelijk vertellen wat de functie moet zijn. Let
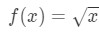
vergelijking 3: schatting met lineaire CA. pt.5 dus we hebben een functie, maar nu hebben we een punt a nodig om mee te werken.,
- Stap 2:
de sleutel tot het vinden van de juiste waarde a is door twee dingen te overwegen:
1) Zorg ervoor dat de waarde a dicht bij x
2) Zorg ervoor dat f(a) een mooi getal is.
zou a = 8 voldoende zijn? Nou, 8 is vrij dicht bij 10 dus het is niet slecht.
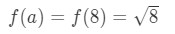
vergelijking 3: schatting met lineaire CA. pt.6 merk op dat 8\sqrt{8}8 geen erg mooi getal is. In feite krijg je een hoop decimale getallen. Dus we moeten iets anders proberen.,
zou a = 9 voldoende zijn? Nogmaals, 9 is vrij dicht bij 10 dus het is oke. Ook

vergelijking 3: schatting met lineaire CA. pt.7 f(a) is eigenlijk een mooi heel getal hier, dus dit werkt echt! Dus a=9 is voldoende.
- Stap 3:
merk op dat uit eerder:

vergelijking 3: schatting met lineaire CA. pt.,8 Calculating f'(x) we have again:

Equation 3: Estimate with linear approx. pt.9 So
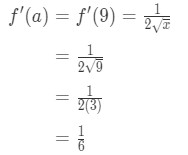
Equation 3: Estimate with linear approx. pt.,10 - Step 4:
Going back to the linear approximation formula we have:

Equation 3: Estimate with linear approx. pt.11 Plugging a, f(a), f'(a), f(x), and x in our formula you will see that:

Equation 3: Estimate with linear approx. pt.12 Hence, we just approximated the number!,
Als u meer oefenproblemen wilt over lineaire benadering, dan raad ik u aan deze link hier te bekijken.
http://tutorial.math.lamar.edu/Classes/CalcI/LinearApproximations.aspx
overschatten en onderschatten
we weten dat lineaire benadering slechts een schatting is van de waarde van de functie op een bepaald punt. Maar hoe weten we dat als onze schatting een overschatting of een onderschatting is? We berekenen de tweede afgeleide en kijken naar de concaviteit.,
Concave up vs Concave down
als de tweede afgeleide van de functie groter is dan 0 voor waarden in de buurt van a, dan is de functie concave up. Dit betekent dat onze benadering een onderschatting zal zijn. Met andere woorden,
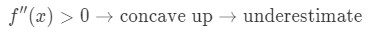
waarom? Laten we eens naar deze grafiek kijken.,
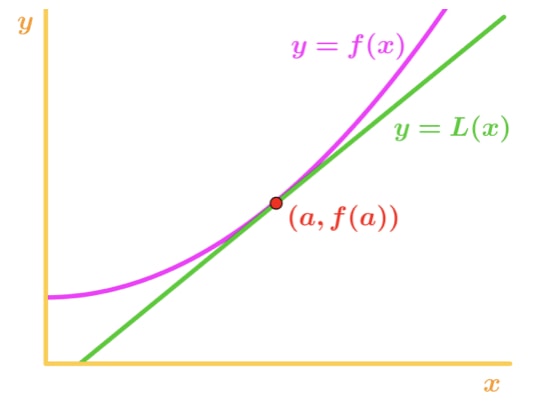
merk op dat f(x) naar boven concaaf is en de raaklijn recht onder f(x) staat. Laten we zeggen dat we de raaklijn gebruiken om f(x) te benaderen. Dan zullen de y-waarden van de raaklijn altijd kleiner zijn dan de werkelijke waarde van f (x). Daarom hebben we nu een onderschatting
als de tweede afgeleide van de functie kleiner is dan 0 voor waarden in de buurt van a, dan is de functie concave naar beneden., Dit betekent dat onze benadering een overschatting zal zijn. Met andere woorden,
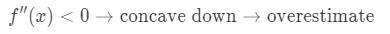
nogmaals, waarom? Laten we een andere grafiek bekijken.
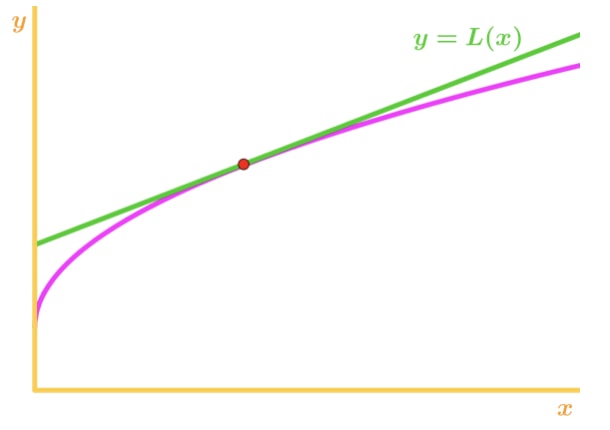
merk op dat f(x) naar beneden concave is en de raaklijn recht boven f(x) ligt. Nogmaals, laten we zeggen dat we de raaklijn gaan gebruiken om F(x) te benaderen., Dan zullen de y-waarden van de raaklijn altijd groter zijn dan de werkelijke waarde van f (x). Daarom hebben we een overschatting.
dus als u ooit wilt zien of uw waarde een onderschatting of een overschatting is, moet u deze stappen volgen:
- Stap 1: Zoek de tweede afgeleide
- Stap 2: Kijk naar de concaviteit van de functie nabij punt A
- Stap 3: Bevestig dat het een onderschatting/overschatting
laten we een voorbeeld bekijken:
vraag 3: Laat f(x) = x\sqrt{x}x en A = 4. Als we lineaire benadering f (4.,04), zou het een overschatting of een onderschatting zijn?
- Stap 1: zie dat
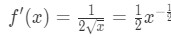
vergelijking 4: overschatting vraag pt.1 dus het tweede derivaat is
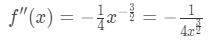
vergelijking 4: overschatting vraag pt.2 - Stap 2:
merk op dat a=4, dus we willen kijken naar positieve waarden van x in de buurt van 4. Kijk nu naar de tweede afgeleide., Als x positief is, zien we dat
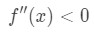
vergelijking 4: overschatting vraag pt.3 daarom is het concave down
- Stap 3:
we weten dat als de functie concave down is, de raaklijn boven de functie zal zijn. Daarom zal het gebruik van de raaklijn als benadering een overschatte waarde opleveren.
Differentialen
niet alleen kunnen we waarden benaderen met lineaire benadering, maar we kunnen ook benaderen met Differentialen., Om te schatten, gebruiken we de volgende formule
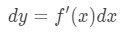
waar dy en dx zijn de verschillen, en f'(x) de afgeleide van f in termen van x. Omdat we te maken hebben met zeer kleine veranderingen in x en y, dan gaan we gebruik maken van het feit dat:
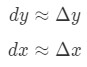
echter, de meeste vragen die we hebben betrekking op het instellen van
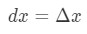
dus het gebruik van deze feiten zal ons leiden tot:
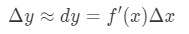
deze benadering is zeer nuttig bij het benaderen van de verandering van y., Houd er rekening mee dat ze toen geen rekenmachines hadden, dus dit is de beste benadering die ze konden krijgen voor functies met vierkantswortels of natuurlijke logs.
Meestal moet je zelf zoeken naar f ‘ (x) en Δ\DeltaΔx. Met andere woorden, volg deze stappen om Δ\DeltaΔy te benaderen!
- Stap 1: Find Δ \ DeltaΔx
- Stap 2: Find f ‘ (x)
- Stap 3: Plug alles in de formule om dy te vinden. dy is de benadering voor Δ\DeltaΔy.
laten we eens kijken naar een voorbeeld van het gebruik van deze benadering:
vraag 4: beschouw de functie y = ln(x + 1)., Stel dat x verandert van 0 naar 0.01. Geschatte Δ\DeltaΔy.
- Stap 1: merk op dat x verandert van 0 naar 0,01, dus de verandering in x zou zijn:
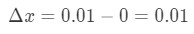
vergelijking 6: Differentiaalvraag pt.1 - Stap 2:
het derivaat zou zijn:
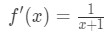
vergelijking 6: Differentiaalvraag pt.,2 - Stap 3:
alles inpluggen wat we hebben:
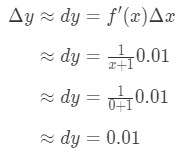
vergelijking 6: Differentiaalvraag pt.3 vandaar, Δ\DeltaΔy ≈\approx≈ 0.01
echter, meestal willen we een waarde van de functie schatten, en niet de verandering van de waarde. Vandaar dat we beide zijden van de vergelijking met y toevoegen, wat ons geeft:
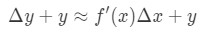
wat hetzelfde is als:
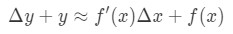
deze vergelijking is een beetje moeilijk te lezen, dus we gaan het nog meer herschikken. Laten we proberen om zich te ontdoen van y En Δ\DeltaΔy. Merk op dat Δ\DeltaΔy + y in principe hetzelfde is als het vinden van de waarde van de functie bij Δ\DeltaΔx+x. met andere woorden,
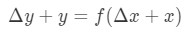
dus als we dit in onze benadering hierboven vervangen, krijgen we:
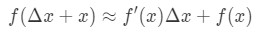
waarbij f(Δ\DeltaΔx+x) de waarde is die we proberen in te schatten. Hoe gebruiken we deze formule? Ik raad aan om deze stappen te volgen:
laten we deze stappen gebruiken voor de volgende vraag.
opdracht 5: Gebruik differentiëlen om ongeveer 10\sqrt{10}10 te benaderen.
- Stap 1: vergelijk f (Δ\DeltaΔx+x) met 10 \ sqrt{10}10., Since 10\sqrt{10}10 has a square root and 9 is a perfect square that is closest to 10, then let
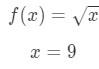
Equation 7: Approximate value with differentials pt.1 Notice that:
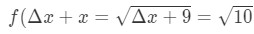
Equation 7: Approximate value with differentials pt.,2 zie dat er geen andere keuze is dan Δ\DeltaΔx = 1
- Stap 2:
zie dat het derivaat geeft:

vergelijking 7: geschatte waarde met differentiëlen pt.3 dus dit impliceert
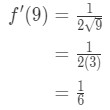
vergelijking 7: geschatte waarde met Differentialen pt.,4 - Stap 3:
alles in de formule steken geeft ons:
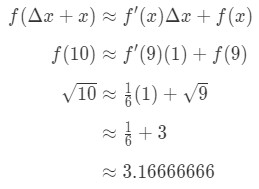
vergelijking 7: geschatte waarde met Differentialen pt.5 daarom benaderden we het getal.
een interessant ding om op te merken is dat lineaire benadering en Differentialen beide hetzelfde resultaat geven voor 10\sqrt{10}10.,
Als u meer wilt weten over Differentialen, klik dan op deze link:
http://tutorial.math.lamar.edu/Classes/CalcI/LinearApproximations.aspx
bewijzen van de regel van L ‘ Hospital met behulp van lineaire benadering
nu hebben we veel geleerd over lineaire benadering, maar wat kunnen we er nog meer mee doen? We kunnen de lineaire benaderingsformule gebruiken om een regel te bewijzen die bekend staat als de regel van L ‘ Hospital . Hier is hoe het bewijs werkt.
bedenk dat de lineaire benaderingsformule is:

zie dat we de formule zo kunnen herschikken dat:
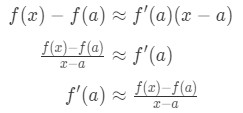
besef dat de benadering steeds nauwkeuriger wordt als we x-waarden kiezen die dichter bij a liggen. met andere woorden, als we de limiet als x→a nemen, dan zullen ze gelijk zijn. So
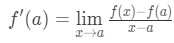
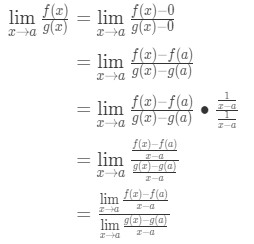
merk nu op dat we hier de formule kunnen toepassen die we eerder hebben afgeleid. Dus nu
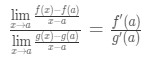
in plaats van F'(A) en g'(a) te schrijven, kunnen we nu limieten toepassen als x→a (omdat we weten dat f en g differentieerbaar zijn)., So
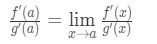
daarom hebben we zojuist aangetoond dat:
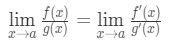
wat de regel van L ‘ Hospital is .
wanneer de regel van l ‘Hopital moet worden gebruikt
We willen altijd de regel van l’ Hopital toepassen wanneer we onbepaalde limieten tegenkomen. Er zijn twee soorten onbepaalde vormen., Deze onbepaalde formulieren zouden zijn:
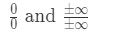
veel mensen maken de fout om de regel van l ‘ Hopital te gebruiken zonder zelfs maar te controleren of het een onbepaalde limiet. Dus zorg ervoor dat u het eerst controleren! Anders zal het niet werken en krijg je het verkeerde antwoord. Hier is een handleiding voor het gebruik van de regel van l ‘ Hopital:
- Stap 1: Evalueer de limiet direct.
- Stap 2: Controleer of het een van de onbepaalde vormen is. Als dat zo is, ga dan naar stap 3.,
- Stap 3: Gebruik de regel van l ‘ Hopital.
- Stap 4: Controleer of u een ander onbepaald formulier krijgt. Herhaal Stap 3 Als u dat doet.
laten we een paar voorbeelden bekijken met behulp van deze stappen.
Vraag 6: Evalueer de limiet
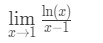
- Stap 1: Het evalueren van de limiet geeft ons direct
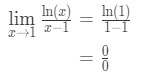
vergelijking 9: L ‘Hopital’ s regelvraag pt.,2 - Stap 2:
Ja, Het is een van de onbepaalde vormen.
- Stap 3:
door de regel van l ‘ Hopital toe te passen hebben we:
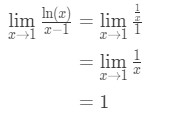
vergelijking 9: L ‘Hopital’ s regelvraag pt.3 - Stap 4:
Eén is geen onbepaalde vorm, dus we zijn klaar en het antwoord is 1.
nu was die vraag een beetje eenvoudig, dus waarom gaan we niet eens kijken naar iets dat een beetje moeilijker is.,
vraag 7: Evalueer de limiet
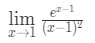
- Stap 1: bij het direct evalueren van de limiet zien we dat:
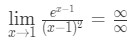
vergelijking 10: L ‘Hopital’ s regel twee keer Vraag pt.2 - Stap 2:
Dit is een onbepaald formulier, dus ga naar stap 3.,
- Stap 3:
door de regel van l ‘ Hopital toe te passen hebben we
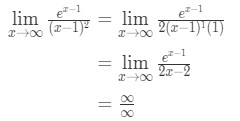
vergelijking 10: L ‘Hopital’ s regel twee keer Vraag pt.3 - Stap 4:
Dit is een andere onbepaalde vorm. Dus moeten we terug naar stap 3 en l ‘hoptial’ s regels opnieuw toepassen.
- Stap 3:
door de regel van l ‘ Hopital opnieuw toe te passen hebben we:
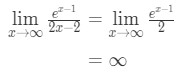
vergelijking 10: L ‘Hopital’ s regel twee keer Vraag pt.,4 - Stap 4:
oneindigheid is geen onbepaalde vorm, dus we zijn klaar en het antwoord is ∞\infty∞