선형 근사값
자의 말하는 일을 잊었 계산기하고 당신이 정말로 원하는 방법을 찾기 위해 무엇을 square root of2 입니다. 계산기가 없으면 어떻게 알 수 있을까요? 우리는 선형 근사를 사용할 수 있습니다!
의 선형화 기능
의 선형화 기능을 막을 찾는 접선의 기능에서 특정 시점에서 다른 방법이다., 선형화 공식은 다음과 같습니다.

L(x)은 방정식의 접라인서점니다.
이것은 어떻게 우리에게 유용하? 글쎄,우리는 실제로이 방정식을 사용하여 점 a 근처의 함수 값을 근사시킬 수 있습니다.이 그래프를 살펴보십시오.,
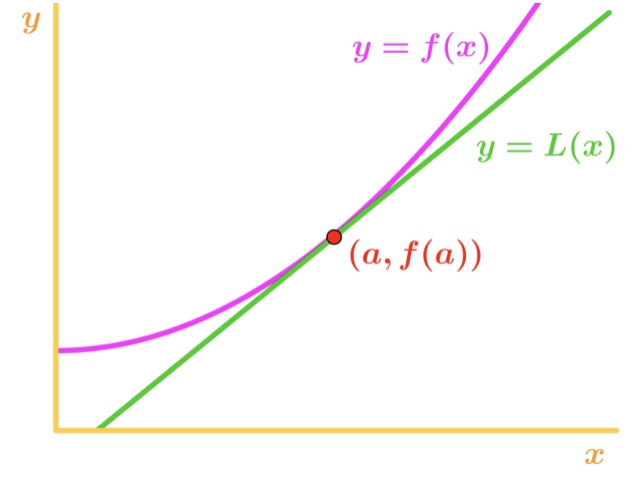
통 x 값을 지점 근처에는,우리는 함수와 접선 상대적으로 가까운 거리에 있습니다. 이 때문에 우리는 함수가 점 a 근처의 접선 선과 거의 같다고 쓸 수 있습니다., 에 다른 단어를,

어디≈\약≈은 약징이다. 이 방정식을 선형 근사 공식으로 알려져 있습니다. 접선이 직선이라는 의미에서 선형이며 함수를 근사하기 위해 사용하고 있습니다. 이 근사치를 사용하여 손으로 할 수없는 값을 근사화 할 수 있습니다. 예를 들어,2 의 제곱근 또는 5 의 자연 로그는 모두 근사 할 수 있습니다!, 하나 중요한 것은 이러 근사치 작동을 위한 x 값이 근처 지점니다. 이 있는 경우 x 값까지 지점에서,다음 근사이 정말 정확하지 않습니다.
이제 우리도 살펴 몇 가지 예의를 찾는 것의 선형화 기능 및 다음 사용하는 방법에 대해 알아 선형 근사값!
찾의 선형화 L(x)의 기능에
질문 1:을 고려한 기능
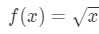
점 a=4 에서 함수의 선형화를 찾고 싶다고 가정 해 봅시다.
선형화 L(x)를 찾으려면

- 1 단계:
- 2 단계:F(a)찾기
- 3 단계:F'(a)찾기.
- 4 단계:세 가지를 모두 수식에 연결하여 L(x)
-
다음 단계를 수행합시다!,
1 단계:운 좋게도 질문에 a=4 가 주어 지므로 찾을 필요가 없습니다.
- 2 단계:
주의
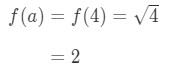
방정식 1:선형화 질문 pt. 3 - 3 단계:
알고 있는 상태에서 사각형 뿌리입니다.
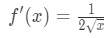
수학식 1:선형화 질문 pt., 4 And so plugging in x=a gives us:
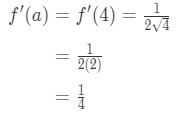
Equation 1: Linearization question pt. 5 - Step 4:
Since we know a, f(a), and f'(a), we can now plug it into L(x) to find the linearization of f(x).
Hence,
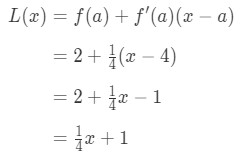
Equation 1: Linearization question pt., 6 그래서 L(x)=14\frac{1}{4}41x+1 은 점 x=4 에서이 함수의 선형화입니다. 또한 점 x=4 에서 함수의 접선 선이기도합니다.
을 어떻게 선형 근사값
이전에 우리는 기억했는 우리가 사용할 수 있는 방정식의 접선하여 대략적인 값의 기능에 가까? 앞에서 찾은 선형화로 이것을 시도해 봅시다.
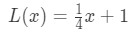
x=4 근처의 점에 대해. 우리는 변경할 수 있으로 선형 근사값 f(x)의 말입니다.
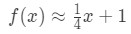
이제 f(4.04)를 근사하고 싶다고 가정 해 봅시다. 이것을 원래 함수에 연결한다면 4.04\sqrt{4.04}4.04 를 얻을 것입니다. 계산기가 없으면 계산하기가 정말 어려울 것입니다., 그러나 사용하여 선형 근사치,우리가 말할 수 있습니다.

지금까지이 질문들은 우리에게 기능과 작업 할 지점을 제공했습니다. 이것들 중 어느 것도 전혀 주어지지 않았다면 어떨까요? 질문이 숫자를 추정하기 만하면 어떨까요?
선형 근사를 사용하여 숫자
10\sqrt{10}10 을 추정하고 싶다고 가정 해보십시오. 우리는 그것을 어떻게 할 것입니까?, 우리는 선형 근사

그러나 우리는 작동 할 함수와 지점조차 가지고 있지 않습니다. 이것은 우리가 그들 자신을 만들어야한다는 것을 의미합니다. 이 우리를 인도하려면 다음 단계를 수행합니다.
- 1 단계:함수 만들기
- 2 단계:을 만들 지점
- 3 단계:찾 f(a)f(a)
- 4 단계:플러그로 모든 것을 선형 근사값식을
의 단계를 따르십시오!,
질문 2:추정 10\sqrt{10}10
- 1 단계:함수를 생각해 봅시다. 우리는
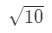
방정식 3:선형 약으로 추정. 태평양 표준시.2 우리는 어떻게 든 f(x)와 10\sqrt{10}10 사이의 관계를 만들어야합니다. 함수가 x 에 종속되지 않기 때문에 f(x)=10\sqrt{10}10 이라고 말할 수 없습니다. 예를 들어,방정식 3 은 선형 추정치 인 약 1b876f7e53 을 곱한 값입니다. 태평양 표준시.,3우리가 할 경우는,그러면 우리는 기본적으로 말하는
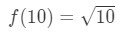
식 3:견적을 가진 선형 approx. 태평양 표준시.4 이제 함수가 무엇이어야하는지 분명히 알 수 있습니다. Let
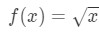
식 3:견적을 가진 선형 approx. 태평양 표준시.5 그래서 우리는 함수를 가지고 있지만,이제는 작업 할 점 a 가 필요합니다.,
- 2 단계:
키를 찾는 오른쪽의 값이를 고려하여 두 가지:
1)있는지 확인하는 값은 가까 x
2)지 확인하 f(a)은 번호입니다.
a=8 이 충분할까요? 글쎄,8 은 10 에 꽤 가깝기 때문에 나쁘지 않습니다. 그러나,
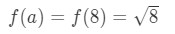
방정식 3:선형 약으로 추정. 태평양 표준시.6 8\sqrt{8}8 은 아주 좋은 숫자가 아니라는 것을 알 수 있습니다. 사실,당신은 십진수의 무리를 얻을. 그래서 우리는 다른 것을 시도해야합니다.,
a=9 가 충분할까요? 다시 말하지만,9 는 10 에 꽤 가깝기 때문에 괜찮습니다. 또한,

방정식 3:선형 약으로 추정. 태평양 표준시.7 f(a)는 실제로 여기에 좋은 전체 번호이므로 실제로 작동합니다! 그래서 a=9 를 고르는 것만으로도 충분합니다.
- 3 단계:
참고로서 이전:

식 3:견적을 가진 선형 approx. 태평양 표준시.,8 Calculating f'(x) we have again:

Equation 3: Estimate with linear approx. pt.9 So
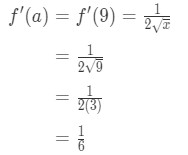
Equation 3: Estimate with linear approx. pt.,10 - Step 4:
Going back to the linear approximation formula we have:

Equation 3: Estimate with linear approx. pt.11 Plugging a, f(a), f'(a), f(x), and x in our formula you will see that:

Equation 3: Estimate with linear approx. pt.12 Hence, we just approximated the number!,
하려면 더 많은 연습 문제에 대해 선형 근사값,그 후에 내가 있는 이 링크에서 여기입니다.
http://tutorial.math.lamar.edu/Classes/CalcI/LinearApproximations.aspx
과대 평가하고 과소 평가
우리가 알고 있는 선형 근사값은 그 추정의 함수의 값을 지정한 지점에서. 그러나 우리의 추정이 과대 평가 또는 과소 평가 인 경우 어떻게 알 수 있습니까? 우리는 두 번째 파생물을 계산하고 오목점을 살펴 봅니다.,
오목 업 대 오목 다운
함수의 두 번째 파생물이 a 근처의 값에 대해 0 보다 큰 경우 함수는 오목 업입니다. 이것은 우리의 근사치가 과소 평가 될 것임을 의미합니다. 에 다른 단어를,
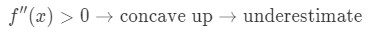
Why? 이 그래프를 살펴 보겠습니다.,
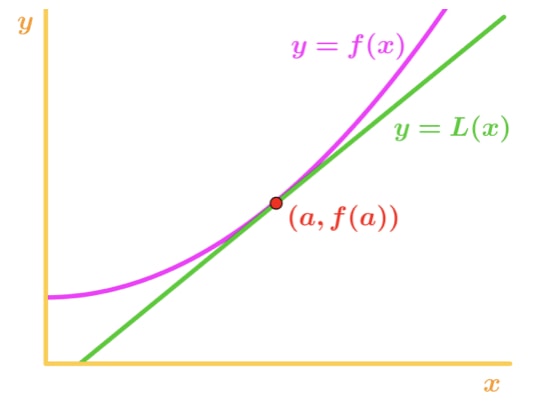
통 f(x)은 오목한 위로와 접선은 오른쪽 아래 f(x) 접선 선을 사용하여 f(x)를 근사화한다고 가정 해 봅시다. 그런 다음 접선 선의 y 값은 항상 f(x)의 실제 값보다 작을 것입니다. 따라서 우리는 과소 평가
이제 함수의 두 번째 파생물이 a 근처의 값에 대해 0 보다 작 으면 함수가 아래로 오목 해집니다., 이것은 우리의 근사치가 과대 평가 될 것임을 의미합니다. 에 다른 단어를,
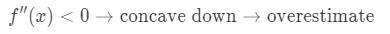
시,왜? 다른 그래프를 살펴 보겠습니다.
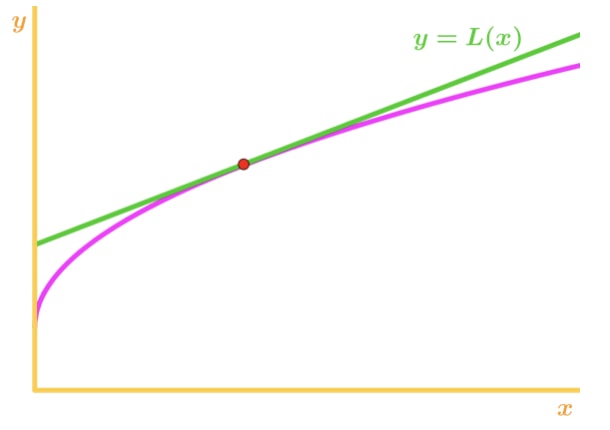
통 f(x)오목 아래와 접선은 오른쪽 위 f(x) 다시 말하지만,접선 선을 사용하여 f(x)를 근사화한다고 가정 해 봅시다., 그런 다음 접선 선의 y 값은 항상 f(x)의 실제 값보다 커질 것입니다. 따라서 우리는 과대 평가를합니다.
그래서 만약 당신이 이제까지 볼 필요가있는 경우에 당신의 값이 과소 평가 또는 인가 과대,확인 이 단계를 따른다:
- 1 단계:찾기 두 번째는 파생
- 2 단계:보면 오목의 기능에 가까운 지점입니다.
- 3 단계: 되었는지 확인하는 과소 평가/을 과대 평가
의 예를 살펴:
질문 3:Let f(x)x=\sqrt{x}x,a=4. 경우 우리는 선형 대략적인 f(4.,04),그것은 과대 평가 또는 과소 평가일까요?
- 1 단계:
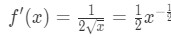
방정식 4:과대 평가 질문 pt.1 그 두 번째는 파생은
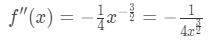
방정식 4:을 과대 평가 질문 pt.2 - 2 단계:
A=4 이므로 4 근처의 x 의 양수 값을보고 싶습니다. 이제 두 번째 파생물을 살펴보십시오., X 이 긍정적이,우리는 것을 볼
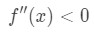
방정식 4:을 과대 평가 질문 pt.3 따라서,그것은 오목한 다운
- 3 단계:
우리가 알고 있는 경우 이 함수는 오목한 다음 접하는 라인이 될 것입니다 위에 있습니다. 따라서 접선 선을 근사치로 사용하면 과대 평가 된 값을 얻게됩니다.
차동
선형 근사치로 값을 근사 할 수있을뿐만 아니라 차동으로 근사 할 수도 있습니다., 를 대략적인,우리가 사용하는 다음 공식
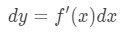
어디 dy 및 dx 는 차이며,f(x)의 유도체 f 측면에서의 x. 때문에 우리가 다루고 있는 아주 작은 변화에서의 x,y,우리는 우리가 사용하는 사실
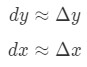
그러나,대부분의 질문에 우리가 포함한 설정
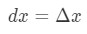
도를 사용하여 이러한 사실이 우리를 이끌가:
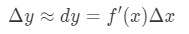
이 근사는 y 의 변화를 근사 할 때 매우 유용합니다., 유지 마음에 다시 다음 그들이 가지고 있지 않은 계산기,이것이 최고의 근사 받을 수 있는지에 대한 기능 사각형 뿌리 또는 천연다.
대부분의 경우 f'(x)와 Δ\DeltaΔx 를 직접 찾아야합니다. 즉,다음 단계에 따라 Δ\DeltaΔy 를 근사화하십시오!
- 1 단계:Δ\DeltaΔx 찾기
- 2 단계:F'(x)찾기
- 3 단계:모든 것을 수식에 연결하여 dy 를 찾습니다. Dy 는 Δ\DeltaΔy 에 대한 근사치가 될 것입니다.
이 근사치를 사용하는 예를 살펴 보겠습니다.
질문 4:함수 y=ln(x+1)을 고려하십시오., X 가 0 에서 0.01 로 변경된다고 가정합니다. 대략적인 Δ\DeltaΔy.
- 1 단계:는지 확 x 에서 변경 0 0.01,so 변 x 이 될 것이다:
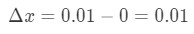
방정식 6:차동 질문 pt.1 - 2 단계:
물이 될 것이다:
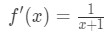
방정식 6:차동 질문 pt.,2 - 3 단계:
연결하는 모든 것에는 우리가
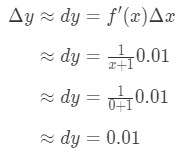
방정식 6:차동 질문 pt.3 따라서,Δ\DeltaΔy≈\약≈0.01
그러나,대부분의 시간을 우리가 원하는 값을 추정하는 기능의,그리고 변화의 값으로 설정합니다. 따라서 우리가 추가됩니다 양쪽의 방정식 y,을 제공합니다:
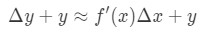
과 동일:
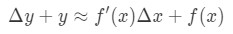
이 방정식을 읽고,그래서 우리는 다시 정렬됩니다. Y 와 Δ\DeltaΔy 를 제거하려고합시다. 알 Δ\DeltaΔy+y 은 기본적으로 같은 가치를 발견의 기능에 Δ\DeltaΔx+x. 에 다른 단어를,
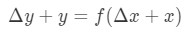
따라서 대체에서 이것은 우리의 근사상 우리에게 줄 것이다:
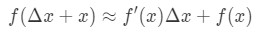
여기서 f(Δ\DeltaΔx+x)는 우리가 추정하려고하는 값입니다. 이 공식을 어떻게 사용합니까? 다음 단계를 따르는 것이 좋습니다.
다음 질문에 대해 다음 단계를 사용하겠습니다.
질문 5:차이를 사용하여 10\sqrt{10}10 을 근사화하십시오.
- 1 단계:F(Δ\DeltaΔx+x)와 10\sqrt{10}10 을 비교합니다., Since 10\sqrt{10}10 has a square root and 9 is a perfect square that is closest to 10, then let
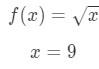
Equation 7: Approximate value with differentials pt.1 Notice that:
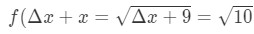
Equation 7: Approximate value with differentials pt.,2 볼 수 없다는 것을 보 Δ\DeltaΔx=1
- 2 단계:
는 파생적인 환산하면 다음과 같습니다.

방정식을 7:대략적인 값을 가진 차이 pt.3 이렇듯
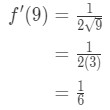
방정식을 7:대략적인 값을 가진 차이 pt.,4 - 3 단계:
연결하는 모든 공식으로 우리를 제공합니다:
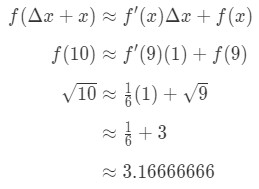
방정식을 7:대략적인 값을 가진 차이 pt.5 따라서 우리는 단지 숫자를 근사했습니다.
한 가지 흥미로운 것은 참고 선형 근사값과 차이 모두 제공에 대해 동일한 결과 10\sqrt{10}10.,
를 배우고 싶다면 더 많은 차이에 대해 이 링크를 클릭하십시오.
http://tutorial.math.lamar.edu/Classes/CalcI/LinearApproximations.aspx
을 증명하 L’Hospital 의 규칙을 사용하여 선형 근사값
이제 우리는 많은 것을 배웠에 대한 선형 근사값만,다른 무엇을 할 수 있을까요? 우리는 실제로 선형 근사 공식을 사용하여 L’Hospital 의 규칙으로 알려진 규칙을 증명할 수 있습니다. 증명이 작동하는 방법은 다음과 같습니다.
리콜는 선형 근사값을 공식은 다음과 같습니다.

을 참조하십시오 우리는 다시 정렬 할 수 있습니다 수식도록:
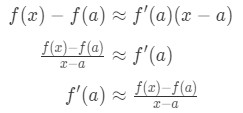
깨닫는 근사치를 더 정확한 것으로 우리가 선택 x 의 값이 있는 가까운다. 다시 말하면 우리의 제한으로 x→,다음 그들이 동일하다. 따라서
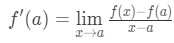
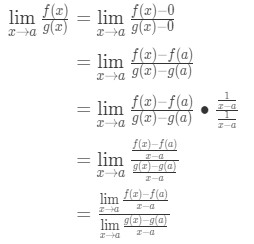
이제는 우리가 적용할 수 있는 수식은 우리는 파생 이전의 바로 여기에 있습니다. 이제
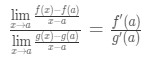
이 쓰는 대신 f(a)g(a),우리 적용할 수 있는 제한으로 x→(기 때문에 우리가 알고 있 f 및 g 는 differentiable)., 따라서
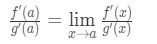
따라서,우리는 그냥 보여주었다.
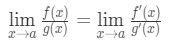
이 L’Hospital 의 규칙이 있습니다.
때 사용하 l’hopital 규
우리는 항상 적용하고 싶 l’hoptial 의 규칙을 때 우리는 불확실한다. 불확정 형태에는 두 가지 유형이 있습니다., 이러한 불확정 형성이 될 것이다:
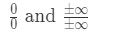
많은 사람들의 실수를 사용하여 l’hopital 규지 않고도 확인하면 그것이 불확실 한계입니다. 그러니 먼저 확인하십시오! 그렇지 않으면 작동하지 않으며 잘못된 대답을 얻을 것입니다. 다음은 l’hopital 의 규칙 사용에 대한 안내서입니다.
- 1 단계:한계를 직접 평가하십시오.
- 2 단계:불확정 양식 중 하나인지 확인하십시오. 그렇다면 3 단계로 이동하십시오.,
- 3 단계:l’hopital 의 규칙을 사용하십시오.
- 4 단계:다른 불확정 양식을 얻는 지 확인하십시오. 그럴 경우 3 단계를 반복하십시오.
이 단계를 사용하여 몇 가지 예를 살펴 보겠습니다.
질문 6:을 평가하 제한
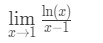
- 1 단계:평가를 제한 직접 우리에게
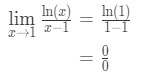
식 9:L’hopital 규 질문 pt.,2 - 2 단계:
예,불확정 형태 중 하나입니다.
- 3 단계:
을 적용하 l’hopital 의 원칙 우리는 가지고있다:
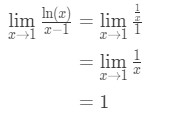
식 9:L’hopital 규 질문 pt.3 - 4 단계:
한가지 확정되지 않은 형태로,그래서 우리가 할 수 있고 대답은 1 입니다.이제 그 질문은 조금 쉬웠습니다.,
질문 7:을 평가하 제한
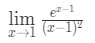
식 10:L’hopital 의 규칙을 두 번 질문 pt.1 - 1 단계:평가하는 한계에 직면 다음과 같습니다.
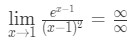
식 10:L’hopital 의 규칙을 두 번 질문 pt.2 - 2 단계:
이것은 불확정 형식이므로 3 단계로 이동하십시오.,
- 3 단계:
을 적용하 l’hopital 의 원칙 우리는 우리가
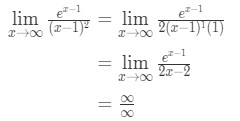
식 10:L’hopital 의 규칙을 두 번 질문 pt.3 - 4 단계:
이것은 또 다른 불확정 형식입니다. 그래서 우리는 3 단계로 돌아가서 l’hoptial 의 규칙을 다시 적용해야합니다.
- 3 단계:
을 적용하 l’hopital 의 규칙을 다시 우리의 전
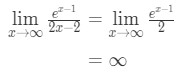
식 10:L’hopital 의 규칙을 두 번 질문 pt.,4 - 4 단계:
무한지 확정되지 않은 형태로,그래서 우리가 할 수 있고 대답은∞\infty∞
- 1 단계:평가하는 한계에 직면 다음과 같습니다.