Approssimazione lineare
Diciamo che un giorno hai dimenticato una calcolatrice e vuoi davvero trovare come è la radice quadrata di 2. Come lo scopriremmo senza una calcolatrice? Possiamo usare l’approssimazione lineare!
Linearizzazione di una funzione
La linearizzazione di una funzione consiste solo nel trovare la linea tangente della funzione in un punto specifico in un modo diverso., La linearizzazione formula è:

dove L(x) è l’equazione della retta tangente nel punto a.
Come sia utile a noi? Bene, possiamo effettivamente usare questa equazione per approssimare i valori della funzione vicino al punto a. Dai un’occhiata a questo grafico.,
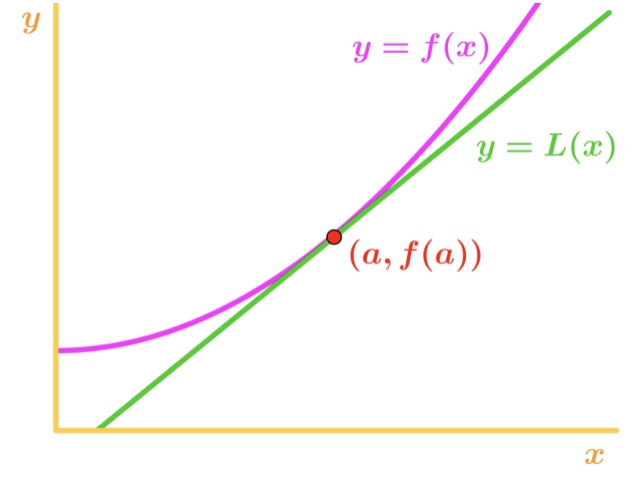
si Noti che per i valori di x in prossimità del punto a, vediamo che la funzione e la retta tangente è relativamente vicino all’altro. Per questo motivo, siamo in grado di scrivere che la funzione è approssimativamente uguale alla linea tangente vicino al punto a., In altre parole,

dove ≈\approx≈ è il simbolo approssimativamente. Questa equazione è conosciuta come la formula di approssimazione lineare. È lineare nel senso che la tangente è una linea retta e la stiamo usando per approssimare la funzione. Usando questa approssimazione, siamo in grado di approssimare valori che non possono essere fatti a mano. Ad esempio, la radice quadrata di 2 o il log naturale di 5 possono essere approssimati!, Una cosa importante da notare è che questa approssimazione funziona solo per i valori x vicino al punto a. Se hai un valore x lontano dal punto a, allora l’approssimazione diventa davvero imprecisa.
Ora non diamo un’occhiata ad alcuni esempi di trovare la linearizzazione di una funzione e poi guardiamo come usare l’approssimazione lineare!
Trova la linearizzazione di L(x) della funzione in una
Domanda 1: Considera la funzione
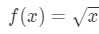
Diciamo che vogliamo trovare la linearizzazione della funzione al punto a=4.
Per trovare la linearizzazione L(x), ricordiamo che

- Passo 1: Trovare un
- Passo 2: Trovare f(a)
- Passo 3: Trovare f'(a).
- Passo 4: Collegare tutti e tre nella formula per trovare L(x)
-
Seguiamo questi passaggi!,
Passo 1: Fortunatamente a = 4 ci viene dato nella domanda, quindi non dobbiamo cercarlo.
- Passo 2:
Si noti che
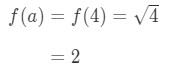
Equazione 1: Domanda di linearizzazione pt. 3 - Passo 3:
Sapere che la derivata delle radici quadrate è
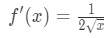
Equazione 1: Domanda di linearizzazione pt., 4 And so plugging in x=a gives us:
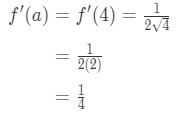
Equation 1: Linearization question pt. 5 - Step 4:
Since we know a, f(a), and f'(a), we can now plug it into L(x) to find the linearization of f(x).
Hence,
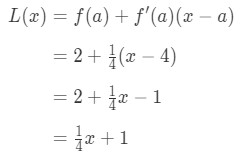
Equation 1: Linearization question pt., 6 Quindi L(x)=14\frac{1}{4}41x+1 è la linearizzazione di questa funzione nel punto x=4. Inoltre, è anche la linea tangente della funzione al punto x = 4.
Come fare approssimazione lineare
Ricordate in precedenza abbiamo detto che potremmo usare l’equazione della retta tangente per approssimare i valori della funzione vicino a? Proviamo questo con la linearizzazione che abbiamo trovato prima. Ricordiamo che
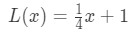
per i punti vicini a x = 4. Possiamo cambiare questo in un’approssimazione lineare per f (x) dicendo che:
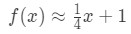
Ora, diciamo che voglio approssimare f(4.04). Se dovessi collegarlo alla funzione originale, otterrai 4.04 \ sqrt{4.04} 4.04 . Questo sarebbe davvero difficile da calcolare senza una calcolatrice., Tuttavia, usando l’approssimazione lineare, possiamo dire che

Ora, queste domande ci hanno dato una funzione e un punto con cui lavorare. Cosa succede se nessuno di questi è stato dato a tutti? Cosa succede se la domanda ci dice solo di stimare un numero?
Usa l’approssimazione lineare per stimare un numero
Supponiamo di voler stimare 10\sqrt{10}10. Come faremmo?, Avremmo bisogno di usare l’approssimazione lineare

ma non abbiamo nemmeno una funzione e un punto con cui lavorare. Questo significa che dobbiamo farli noi stessi. Questo ci porta a fare i seguenti passi:
- Passo 1: creare una funzione
- Passo 2: creare il punto a
- Passo 3: Trovare f(a) e f'(a)
- Passo 4: Collegare tutto nella formula di approssimazione lineare
Seguiamo i passaggi!,
Domanda 2: Stima 10\sqrt{10}10
- Passo 1: Troviamo una funzione. Si noti che stiamo stimando
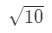
Equazione 3: Stima con lineare ca. PT.2 Dobbiamo in qualche modo creare una relazione tra f(x) e 10\sqrt{10}10. Non possiamo dire che f (x) = 10 \ sqrt{10}10 perché la funzione non dipenderà da x. Quindi perché non lo facciamo? Let
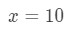
Equazione 3: Stima con lineare ca. PT.,3 Se lo facciamo, stiamo fondamentalmente dicendo
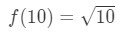
Equazione 3: Stima con lineare ca. PT.4 Ora possiamo ovviamente dire quale dovrebbe essere la funzione. Let
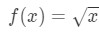
Equazione 3: Stima con lineare ca. PT.5 Quindi abbiamo una funzione, ma ora abbiamo bisogno di un punto a con cui lavorare.,
- Passo 2:
La chiave per trovare il giusto valore a è considerando due cose:
1) Assicurati che il valore a sia vicino a x
2) Assicurati che f(a) sia un bel numero.
A = 8 sarebbe sufficiente? Bene, 8 è abbastanza vicino a 10 quindi non è male. Tuttavia,
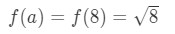
Equazione 3: Stima con lineare ca. PT.6 Si noti che 8\sqrt{8}8 non è un numero molto bello. In effetti, ottieni un sacco di numeri decimali. Quindi dobbiamo provare qualcos’altro.,
A = 9 sarebbe sufficiente? Ancora una volta, 9 è abbastanza vicino a 10 quindi va bene. Inoltre,

Equazione 3: Stima con lineare ca. PT.7 f(a) è in realtà un bel numero intero qui, quindi funziona davvero! Quindi scegliere a = 9 è abbastanza sufficiente.
- Passo 3:
Si noti che da prima:

Equazione 3: Stima con lineare ca. PT.,8 Calculating f'(x) we have again:

Equation 3: Estimate with linear approx. pt.9 So
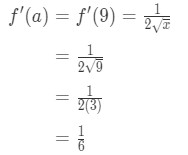
Equation 3: Estimate with linear approx. pt.,10 - Step 4:
Going back to the linear approximation formula we have:

Equation 3: Estimate with linear approx. pt.11 Plugging a, f(a), f'(a), f(x), and x in our formula you will see that:

Equation 3: Estimate with linear approx. pt.12 Hence, we just approximated the number!,
Se vuoi più problemi di pratica sull’approssimazione lineare, ti consiglio di guardare questo link qui.
http://tutorial.math.lamar.edu/Classes/CalcI/LinearApproximations.aspx
Sopravvalutare e Sottovalutare
Sappiamo che l’approssimazione lineare è solo una stima del valore della funzione in un punto specificato. Tuttavia, come facciamo a sapere che se la nostra stima è una sovrastima o una sottovalutazione? Calcoliamo la derivata seconda e guardiamo la concavità.,
Concavo up vs Concavo down
Se la derivata seconda della funzione è maggiore di 0 per i valori vicini a, la funzione è concava up. Ciò significa che la nostra approssimazione sarà una sottovalutazione. In altre parole,
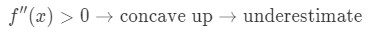
Perché? Diamo un’occhiata a questo grafico.,
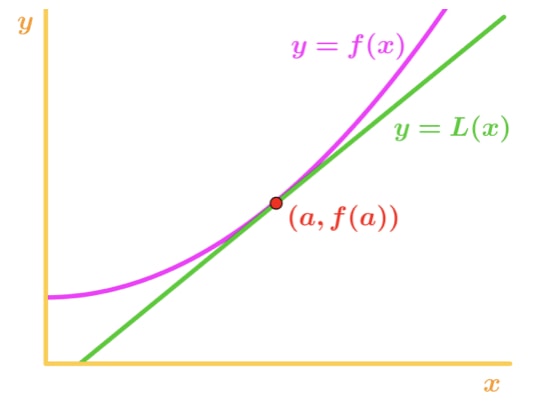
Si noti che f(x) è concavo verso l’alto e la linea tangente è proprio sotto f(x). Diciamo che dovevano usare la linea tangente per approssimare f (x). Quindi i valori y della linea tangente saranno sempre inferiori al valore effettivo di f (x). Quindi, abbiamo una sottostima
Ora se la derivata seconda della funzione è inferiore a 0 per i valori vicini a, allora la funzione è concava verso il basso., Ciò significa che la nostra approssimazione sarà una sovrastima. In altre parole,
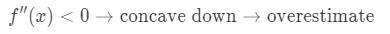
Ancora una volta, perché? Diamo un’occhiata a un altro grafico.
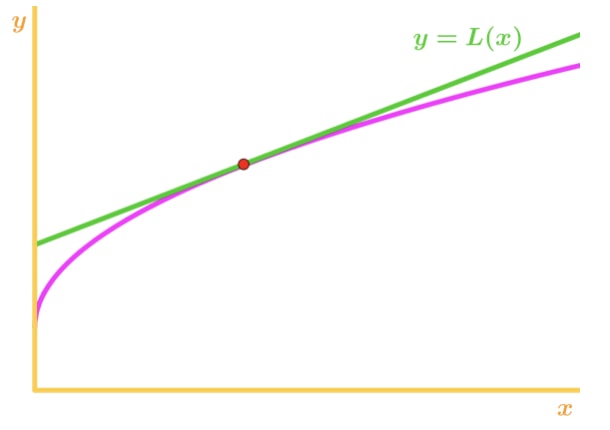
Si noti che f (x) è concavo verso il basso e la linea tangente è proprio sopra f (x). Di nuovo, diciamo che useremo la linea tangente per approssimare f (x)., Quindi i valori y della linea tangente saranno sempre maggiori del valore effettivo di f (x). Quindi, abbiamo una sovrastima.
Quindi, se mai bisogno di vedere se il valore è una sottostima o sovrastima, assicurarsi di seguire questi passi:
- Passo 1: Trovare la derivata seconda
- Passo 2: guardate la concavità della funzione vicino a punto di un
- Step 3: Confermare che si tratta di una sottostima/sovrastima
diamo un’occhiata a un esempio:
Domanda 3: sia f(x) = x\sqrt{x}x e = 4. Se abbiamo approssimativo lineare f (4.,04), sarebbe una sopravvalutazione o una sottovalutazione?
- Passo 1: Vedere che
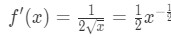
Equazione 4: Sovrastima domanda pt.1 Quindi la derivata seconda è
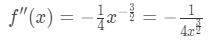
Equazione 4: Sovrastima domanda pt.2 - Passo 2:
Si noti che a = 4, quindi vogliamo guardare i valori positivi di x vicino a 4. Ora guarda la seconda derivata., Quando x è positivo, vediamo che
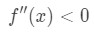
Equazione 4: Sovrastima domanda pt.3 Quindi, è concavo verso il basso
- Passo 3:
Sappiamo che se la funzione è concava verso il basso, quindi la linea tangente sarà al di sopra della funzione. Quindi, usando la linea tangente come approssimazione darà un valore sovrastimato.
Differenziali
Non solo possiamo approssimare i valori con approssimazione lineare, ma possiamo anche approssimare con differenziali., Per approssimare, si utilizza la seguente formula
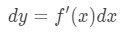
dove dx e dy sono differenziali, e f'(x) è la derivata di f in termini di x. Dal momento che abbiamo a che fare con dei piccoli cambiamenti in x e y, quindi abbiamo intenzione di utilizzare il fatto che:
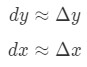
Tuttavia, la maggior parte delle domande riguardano l’impostazione
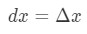
Quindi l’uso di questi fatti ci porterà ad avere:
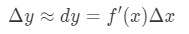
Questa approssimazione è molto utile quando si approssima il cambiamento di y., Tieni presente che allora non avevano calcolatrici, quindi questa è la migliore approssimazione che potevano ottenere per funzioni con radici quadrate o registri naturali.
La maggior parte delle volte dovrai cercare f'(x) e Δ\DeltaΔx da solo. In altre parole, seguire questi passaggi per approssimare Δ \ DeltaΔy!
- Passo 1: Trova Δ\DeltaΔx
- Passo 2: Trova f'(x)
- Passo 3: Collega tutto nella formula per trovare dy. dy sarà l’approssimazione per Δ \ DeltaΔy.
Diamo un’occhiata a un esempio di utilizzo di questa approssimazione:
Domanda 4: Considera la funzione y = ln(x + 1)., Supponiamo che x cambi da 0 a 0.01. Δ\DeltaΔy approssimativo.
- Passo 1: Si noti che x cambia da 0 a 0.01, quindi il cambiamento in x sarebbe:
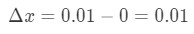
Equazione 6: Domanda differenziale pt.1 - Passo 2:
La derivata sarebbe:
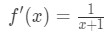
Equazione 6: Domanda differenziale pt.,2 - Passo 3:
Collegare tutto abbiamo:
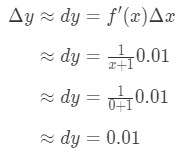
Equazione 6: Domanda differenziale pt.3 Quindi, Δ\DeltaΔy ≈\approx≈ 0.01
Tuttavia, il più delle volte vogliamo stimare un valore della funzione e non la modifica del valore. Quindi aggiungeremo entrambi i lati dell’equazione per y, che ci dà:
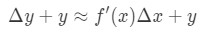
che è lo stesso di:
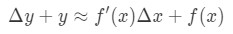
Questa equazione è un po ‘ difficile da leggere, quindi la riorganizzeremo ancora di più. Proviamo a sbarazzarci di y e Δ \ DeltaΔy. Si noti che Δ\DeltaΔy+ y è fondamentalmente lo stesso di trovare il valore della funzione a Δ \ DeltaΔx + x. In altre parole,
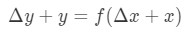
Quindi la sostituzione di questo nella nostra approssimazione sopra ci darà:
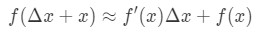
dove f(Δ\DeltaΔx+x) è il valore che stiamo cercando di stimare. Come usiamo questa formula? Raccomando di seguire questi passaggi:
Usiamo questi passaggi per la seguente domanda.
Domanda 5: Usa i differenziali per approssimare 10 \ sqrt{10}10.
- Passo 1: Confrontare f(Δ \ DeltaΔx + x) con 10\sqrt{10}10., Since 10\sqrt{10}10 has a square root and 9 is a perfect square that is closest to 10, then let
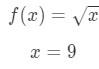
Equation 7: Approximate value with differentials pt.1 Notice that:
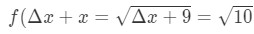
Equation 7: Approximate value with differentials pt.,2 Guarda che non c’è scelta, ma per far Δ\DeltaΔx = 1
- Passo 2:
Vedere che la derivata si ottiene:

Equazione 7: valore Approssimato con differenziali pt.3 Quindi questo implica
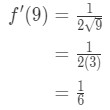
Equazione 7: Valore approssimativo con differenziali pt.,4 - Passo 3:
Collegare tutto nella formula ci dà:
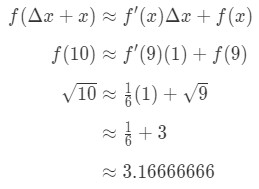
Equazione 7: Valore approssimativo con differenziali pt.5 Quindi, abbiamo appena approssimato il numero.
Una cosa interessante da notare è che l’approssimazione lineare e i differenziali danno entrambi lo stesso risultato per 10\sqrt{10}10.,
Se vuoi saperne di più sui differenziali, fai clic su questo link:
http://tutorial.math.lamar.edu/Classes/CalcI/LinearApproximations.aspx
Dimostrando la regola dell’Ospedale usando l’approssimazione lineare
Ora abbiamo imparato molto sull’approssimazione lineare, ma cos’altro possiamo fare con essa? Possiamo effettivamente usare la formula di approssimazione lineare per dimostrare una regola nota come Regola di L’Hospital . Ecco come funziona la prova.
Ricordiamo che la formula di approssimazione lineare è:

Vediamo che possiamo riorganizzare la formula in modo che:
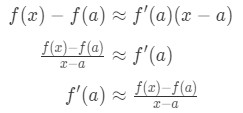
Renditi conto che l’approssimazione diventa sempre più accurata quando selezioniamo i valori x più vicini ad a. In altre parole, se prendiamo il limite come x→a, allora saranno uguali. Quindi
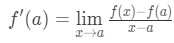
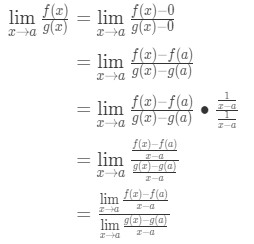
Ora si noti che possiamo applicare la formula che abbiamo derivato in precedenza proprio qui. Quindi ora
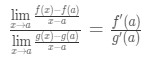
Ora invece di scrivere f'(a) e g'(a), possiamo applicare i limiti come x→a (perché sappiamo che f e g sono differenziabili)., Quindi
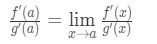
Quindi, abbiamo appena mostrato che:
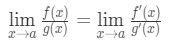
che è la Regola di l’Hospital .
Quando usare la regola di l’hopital
Vogliamo sempre applicare la regola di l’hoptial quando incontriamo limiti indeterminati. Esistono due tipi di forme indeterminate., Queste forme indeterminate sarebbero:
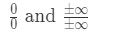
Molte persone commettono l’errore di usare l’hopital regola senza nemmeno controllare se si tratta di un limite indeterminato. Quindi assicuratevi di controllare prima! Altrimenti, non funzionerà e otterrai la risposta sbagliata. Ecco una guida per usare la regola di l’hopital:
- Passo 1: Valuta direttamente il limite.
- Passo 2: Controlla se è una delle forme indeterminate. Se lo è, vai al passaggio 3.,
- Passo 3: Usa la regola di l’hopital.
- Passo 4: Controlla se ottieni un altro modulo indeterminato. Ripetere il passaggio 3 se lo fai.
Diamo un’occhiata ad alcuni esempi utilizzando questi passaggi.
Domanda 6: Valutare il limite
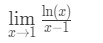
- Passo 1: Valutare il limite ci dà direttamente
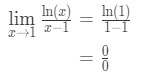
Equazione 9:La regola di L’hopital domanda pt.,2 - Passo 2:
Sì, è una delle forme indeterminate.
- Passo 3:
Applicando la regola di l’hopital abbiamo:
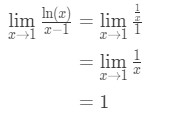
Equazione 9: La regola di L’hopital domanda pt.3 - Passo 4:
uno non è una forma indeterminata, quindi abbiamo finito e la risposta è 1.
Ora quella domanda era un po ‘facile, quindi perché non diamo un’occhiata a qualcosa che è un po’ più difficile.,
Domanda 7: Valuta il limite
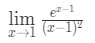
- Passo 1: Valutare direttamente il limite vediamo che:
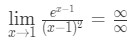
Equazione 10: La regola di L’hopital due volte domanda pt.2 - Passaggio 2:
Questa è una forma indeterminata, quindi vai al passaggio 3.,
- Passo 3:
Applicando la regola di l’hopital abbiamo
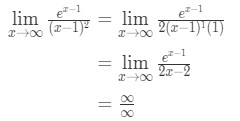
Equazione 10: La regola di L’hopital due volte domanda pt.3 - Passo 4:
Questa è un’altra forma indeterminata. Quindi dobbiamo tornare al punto 3 e applicare di nuovo le regole di l’optial.
- Passo 3:
Applicando di nuovo la regola di l’hopital abbiamo:
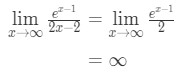
Equazione 10: La regola di L’hopital due volte domanda pt.,4 - Passo 4:
L’infinito non è una forma indeterminata, quindi abbiamo finito e la risposta è ∞\infty∞