Approximation linéaire
disons qu’un jour vous avez oublié une calculatrice et que vous voulez vraiment trouver comment est la racine carrée de 2. Comment le trouverions-nous sans calculatrice? Nous pouvons utiliser l’approximation linéaire!
la Linéarisation d’une fonction
La linéarisation de la fonction est juste de trouver la tangente de la fonction en un point précis d’une manière différente., La linéarisation de la formule est:

où L(x) est l’équation de la tangente au point d’un.
Comment est-ce utile pour nous? Eh bien, nous pouvons réellement utiliser cette équation pour approximer les valeurs de la fonction près du point a. Regardez ce graphique. ,
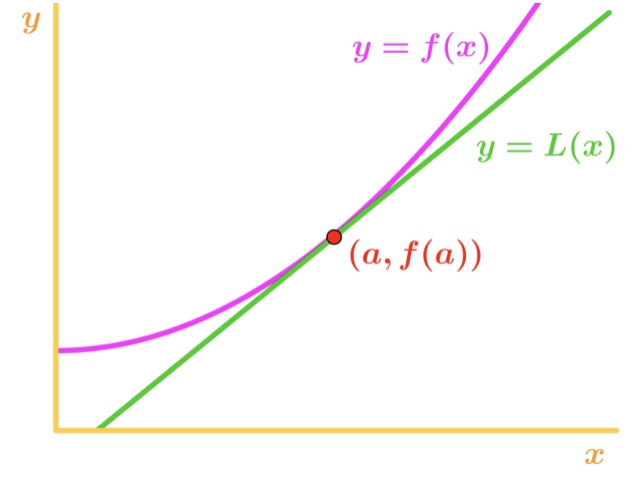
Notez que pour les valeurs de x à proximité d’un point, nous voyons que la fonction et la tangente est relativement proches les uns des autres. Pour cette raison, nous pouvons écrire que la fonction est approximativement égale à la ligne tangente près du point a., En d’autres termes,

où ≈\approx≈ est la environ symbole. Cette équation est connue sous le nom de formule d’approximation linéaire. Elle est linéaire dans le sens où la tangente est une droite et nous l’utilisons pour approximer la fonction. En utilisant cette approximation, nous sommes en mesure d’approximer des valeurs qui ne peuvent pas être faites à la main. Par exemple, la racine carrée de 2 ou le log naturel de 5 peuvent tous être approximés!, Une chose importante à noter est que cette approximation ne fonctionne que pour les valeurs x proches du point A. Si vous avez une valeur x loin du point a, l’approximation devient vraiment inexacte.
Maintenant, ne pas nous jeter un oeil à quelques exemples de trouver la linéarisation de la fonction, puis regardez comment utiliser l’approximation linéaire!
Trouver la linéarisation de L(x) de la fonction à la une
Question 1: Considérons la fonction
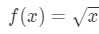
disons que nous voulons trouver la linéarisation de la fonction en un point a=4.
Pour trouver la linéarisation L(x), rappelle que

- Étape 1: Trouver un
- Étape 2: Trouver f(a)
- Étape 3: Trouver f'(a).
- Étape 4: Branchez tous les trois dans la formule pour trouver L(x)
-
nous allons suivre ces étapes!,
Étape 1: heureusement, a = 4 nous est donné dans la question, donc nous n’avons pas à le chercher.
- Etape 2:
Notez que
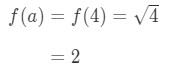
l’Équation 1: Linéarisation question pt. 3 - Etape 3:
Savez que les dérivés de racines carrées est
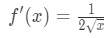
l’Équation 1: Linéarisation question pt., 4 And so plugging in x=a gives us:
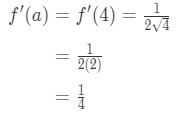
Equation 1: Linearization question pt. 5 - Step 4:
Since we know a, f(a), and f'(a), we can now plug it into L(x) to find the linearization of f(x).
Hence,
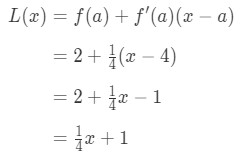
Equation 1: Linearization question pt., 6 Donc L(x)=14\frac{1}{4}41x+1 est la linéarisation de cette fonction au point x=4. De plus, c’est aussi la ligne tangente de la fonction au point x=4.
Comment faire une approximation linéaire
rappelez-vous que nous avons dit plus tôt que nous pourrions utiliser l’équation de la ligne tangente pour approximer les valeurs de la fonction près de a? Essayons ceci avec la linéarisation que nous avons trouvée plus tôt. Rappelons que
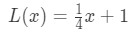
pour les points près de x=4. Nous pouvons changer cela dans une approximation linéaire de f(x) en disant:
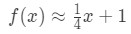
Maintenant, disons que je veux approximation de f(4.04). Si vous deviez brancher cela dans la fonction d’origine, vous obtiendrez 4.04 \ sqrt{4.04}4.04 . Ce serait vraiment difficile à calculer sans calculatrice., Cependant, l’utilisation d’approximation linéaire, nous pouvons dire que

Maintenant, jusqu’à présent, ces questions nous ont donné une fonction et un point à travailler. Que faire si aucune de ces ont été donnés à tous? Et si la question nous dit seulement d’estimer un nombre?
Utiliser l’approximation Linéaire pour estimer un nombre
Supposons que nous voulons estimer à 10\sqrt{10}10. Comment pourrions-nous le faire?, Nous aurions besoin d’utiliser l’approximation linéaire

mais nous n’avons même pas une fonction et un point à travailler. Cela signifie que nous devons faire nous-mêmes. Cela nous amène à faire les étapes suivantes:
- Étape 1: Créer une fonction
- Étape 2: Créer un point a
- Étape 3: Trouver f(a) et f'(a)
- Étape 4: Branchez tout dans la formule d’approximation linéaire
suivons les étapes!,
Question 2: Estimation de 10\sqrt{10}10
- Étape 1: nous allons venir avec une fonction. Notez que nous sommes à l’estimation de
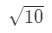
Équation 3: Estimation linéaire environ. PT.2 nous devons en quelque sorte établir une relation entre f(x) et 10\sqrt{10}10. Nous ne pouvons pas dire que f(x) = 10\sqrt{10}10 car la fonction ne dépendra pas de X. Alors pourquoi ne faisons-nous pas cela? Laissez
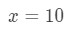
Équation 3: Estimation linéaire environ. PT.,3 Si nous le faisons, nous sommes fondamentalement en disant:
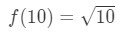
Équation 3: Estimation linéaire environ. PT.4 nous pouvons maintenant évidemment dire quelle devrait être la fonction. Laissez
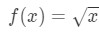
Équation 3: Estimation linéaire environ. PT.5 nous avons Donc une fonction, mais maintenant nous avons besoin d’un point a à travailler avec.,
- Etape 2:
La clé pour trouver la valeur de a est en prenant en compte deux choses:
1) assurez-vous que la valeur est proche de x
2) assurez-vous que f(a) est un joli nombre.
a = 8 serait-il suffisant? Eh bien, 8 est assez proche de 10 donc ce n’est pas mal. Cependant,
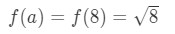
Équation 3: Estimation linéaire environ. PT.6 Notez qu’8\sqrt{8}8 n’est pas un très bon nombre. En fait, vous obtenez un tas de nombres décimaux. Nous avons donc essayer autre chose.,
a = 9 serait-il suffisant? Encore une fois, 9 est assez proche de 10, donc ça va. Aussi,

Équation 3: Estimation linéaire environ. PT.7 f(a) est en fait un bon nombre entier ici, donc cela fonctionne réellement! Donc, choisir a = 9 est suffisant.
- Etape 3:
Notez que de plus en plus tôt:

Équation 3: Estimation linéaire environ. PT.,8 Calculating f'(x) we have again:

Equation 3: Estimate with linear approx. pt.9 So
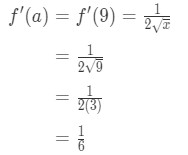
Equation 3: Estimate with linear approx. pt.,10 - Step 4:
Going back to the linear approximation formula we have:

Equation 3: Estimate with linear approx. pt.11 Plugging a, f(a), f'(a), f(x), and x in our formula you will see that:

Equation 3: Estimate with linear approx. pt.12 Hence, we just approximated the number!,
Si vous voulez plus de pratique des problèmes d’approximation linéaire, alors je vous recommande de regarder ce lien ici.
http://tutorial.math.lamar.edu/Classes/CalcI/LinearApproximations.aspx
surestimer et sous-estimer
Nous savons que l’approximation linéaire n’est qu’une estimation de la valeur de la fonction à un point spécifié. Cependant, comment savons-nous que si notre estimation est une surestimation ou une sous-estimation? Nous calculons la dérivée seconde et regardons la concavité.,
Concave jusqu’vs Concave vers le bas
Si la dérivée seconde de la fonction est supérieure à 0 pour les valeurs proches de a, alors la fonction est concave vers le haut. Cela signifie que notre approximation sera une sous-estimation. En d’autres termes,
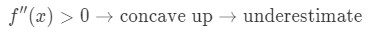
Pourquoi? Jetons un coup d’oeil à ce graphique.,
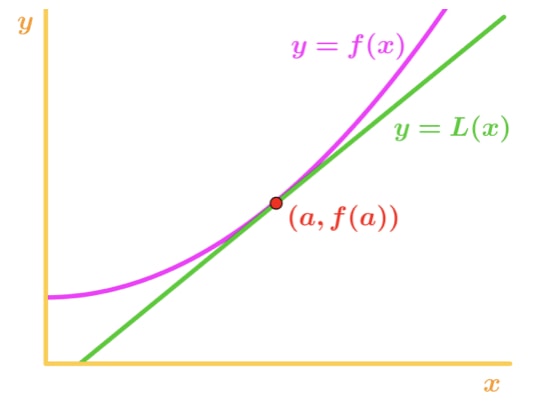
Notez que f(x) est concave vers le haut et la tangente de la ligne juste en-dessous de f(x). Disons qu’il fallait utiliser la ligne tangente pour approximer f (x). Ensuite, les valeurs y de la ligne tangente seront toujours inférieures à la valeur réelle de f(x). Par conséquent, nous avons une sous-estimation
maintenant si la dérivée seconde de la fonction est inférieure à 0 pour les valeurs proches de a, alors la fonction est concave vers le bas., Cela signifie que notre approximation sera une surestimation. En d’autres termes,
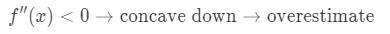
Encore une fois, pourquoi? Jetons un coup d’oeil à un autre graphique.
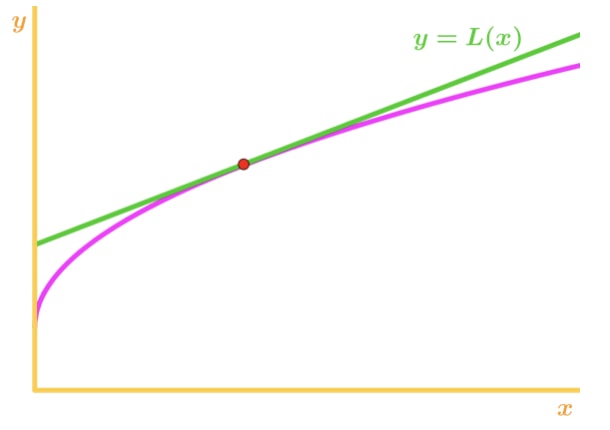
Notez que f(x) est concave vers le bas et la tangente est la droite au-dessus de f(x). Encore une fois, disons que nous allons utiliser la ligne tangente pour approximer f(x)., Ensuite, les valeurs y de la ligne tangente seront toujours supérieures à la valeur réelle de f(x). Par conséquent, nous avons une surestimation.
donc, si jamais vous avez besoin de voir si votre valeur est une sous-estimation ou une surestimation, assurez-vous de suivre ces étapes:
- Étape 1: Trouver la dérivée seconde
- Étape 2: regardez la concavité de la fonction près du point a
- Étape 3: confirmez qu’il s’agit d’une sous-estimation/surestimation
x) = x\sqrt{x}x et a = 4. Si nous approximons linéaire f (4.,04), serait-il une surestimation ou une sous-estimation?
- Étape 1: Voir à ce que
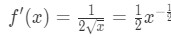
l’Équation 4: Surestimer la question pt.1 Donc la dérivée seconde est
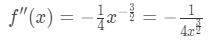
l’Équation 4: Surestimer la question pt.2 - Étape 2:
notez que a=4, nous voulons donc regarder les valeurs positives de x proches de 4. Maintenant, regardez la dérivée seconde., Lorsque x est positif, nous voyons que
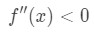
l’Équation 4: Surestimer la question pt.3 par conséquent, il est concave vers le bas
- Etape 3:
Nous savons que si la fonction est concave vers le bas, puis la tangente sera au-dessus de la fonction. Par conséquent, l’utilisation de la ligne tangente comme approximation donnera une valeur surestimée.
différentiels
non seulement nous pouvons approximer les valeurs avec une approximation linéaire, mais nous pouvons également approximer avec des différentiels., Pour approximer, nous utilisons la formule suivante
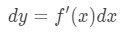
où dy et dx sont des différentiels, et f'(x) est le dérivée de f en termes de X. puisque nous avons affaire à de très petits changements dans X et Y, alors nous allons utiliser le fait que:
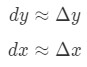
Cependant, la plupart des questions que nous ne nous impliquer la création d’
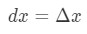
Donc, en utilisant ces faits nous amènent à avoir:
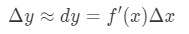
cette approximation est très utile lors de l’approximation du changement de Y., Gardez à l’esprit à l’époque, ils n’avaient pas de calculatrices, c’est donc la meilleure approximation qu’ils pouvaient obtenir pour les fonctions avec des racines carrées ou des journaux naturels.
la plupart du temps, vous devrez rechercher vous-même f'(x) Et Δ\DeltaΔx. En d’autres termes, suivez ces étapes pour approximer Δ\DeltaΔy!
- Étape 1: Trouver Δ\DeltaΔx
- Étape 2: Trouver f'(x)
- Étape 3: Branchez le tout dans la formule pour trouver dy. dy sera l’approximation de Δ \ DeltaΔy.
prenons un exemple d’utilisation de cette approximation:
Question 4: Considérons la fonction y = ln(x + 1)., Supposons que x passe de 0 à 0,01. Approximative Δ \ DeltaΔy.
- Étape 1: notez que x passe de 0 à 0.01, donc le changement dans x serait:
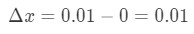
équation 6: Question différentielle pt.1 - Etape 2:
La dérivée serait:
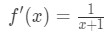
l’Équation (6): Différentiel question pt.,2 - Etape 3:
Brancher tout ce que nous avons:
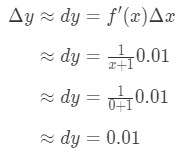
l’Équation (6): Différentiel question pt.3 par conséquent, Δ\DeltaΔy ≈\approx≈ 0.01
Cependant, la plupart du temps, nous voulons estimer une valeur de la fonction, et non pas le changement de la valeur. Par conséquent, nous allons ajouter les deux côtés de l’équation par y, ce qui nous donne:
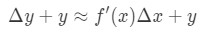
qui est le même que:
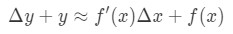
Cette équation est un peu dur à lire, donc nous allons réorganiser encore plus. Essayons de nous débarrasser de y et Δ\DeltaΔy. Notez que Δ \ DeltaΔy + y est fondamentalement la même chose que de trouver la valeur de la fonction à Δ \ DeltaΔx+X. En d’autres termes,
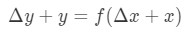
Donc en substituant dans notre approximation ci-dessus va nous donner:
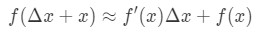
où f(Δ\DeltaΔx+x) est la valeur que nous essayons d’estimation. Comment pouvons-nous utiliser cette formule? Je recommande de suivre ces étapes:
utilisons ces étapes pour la question suivante.
Question 5: Utilisez les différentiels pour approximer 10\sqrt{10}10.
- Étape 1: comparer f(Δ\DeltaΔx+x) avec 10\sqrt{10}10., Since 10\sqrt{10}10 has a square root and 9 is a perfect square that is closest to 10, then let
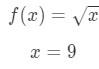
Equation 7: Approximate value with differentials pt.1 Notice that:
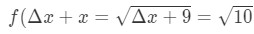
Equation 7: Approximate value with differentials pt.,2 voir qu’il n’y a pas d’autre choix que de laisser Δ\DeltaΔx = 1
- Étape 2:
voir que la dérivée donne:

équation 7: valeur approximative avec différentiels pt.3 Donc cela implique
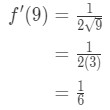
l’Équation 7: valeur Approximative avec des différentiels de pt.,4 - Etape 3:
Brancher le tout dans la formule nous donne:
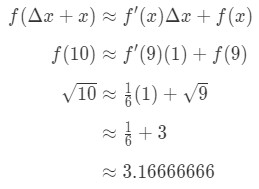
l’Équation 7: valeur Approximative avec des différentiels de pt.5 par conséquent, nous avons juste approchée du nombre.
Une chose intéressante à noter est que l’approximation linéaire et les différentiels donnent le même résultat pour 10\sqrt{10}10.,
Si vous souhaitez en savoir plus sur les différentiels, cliquez sur ce lien:
http://tutorial.math.lamar.edu/Classes/CalcI/LinearApproximations.aspx
Prouvant L’Hospital de la Règle à l’aide approximation linéaire
Maintenant, nous avons beaucoup appris sur l’approximation linéaire, mais quoi d’autre pouvons-nous faire? Nous pouvons en fait utiliser la formule d’approximation linéaire pour prouver une règle connue sous le nom de règle de l’Hôpital . Voici comment fonctionne la preuve.
rappelons que la formule d’approximation linéaire est:

Voyons que nous pouvons réorganiser la formule de la sorte:
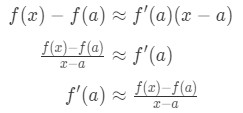
réalisez que l’approximation devient de plus en plus précise à mesure que nous choisissons des valeurs x plus proches de A. en d’autres termes, si nous prenons la limite comme x→a, alors elles seront égales. Donc
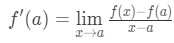
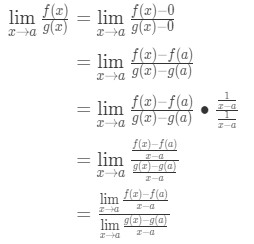
Maintenant, remarquez que nous pouvons appliquer la formule que nous avons obtenues plus tôt ici. Alors maintenant
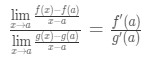
maintenant, au lieu d’écrire f'(a) et g'(A), Nous pouvons appliquer des limites comme x→a (car nous savons que f et g sont différentiables)., Donc
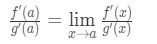
par conséquent, nous avons juste montré que:
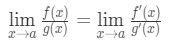
ce qui est la Règle de l’Hospital .
quand utiliser la règle de l’Hopital
nous voulons toujours appliquer la règle de l’hoptial lorsque nous rencontrons des limites indéterminées. Il existe deux types de formes indéterminées., Ces indéterminée formes serait:
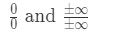
beaucoup de gens font l’erreur d’utiliser l’hopital de la règle, sans même vérifier si c’est une limite de durée indéterminée. Donc, assurez-vous de vérifier d’abord! Sinon, cela ne fonctionnera pas et vous obtiendrez la mauvaise réponse. Voici un guide pour utiliser la règle de l’hôpital:
- Étape 1: évaluer directement la limite.
- Étape 2: Vérifiez s’il s’agit d’une des formes indéterminées. Si elle l’est, passez à l’étape 3.,
- Étape 3: Utilisez la règle de l’hôpital.
- Étape 4: Vérifiez si vous obtenez un autre formulaire indéterminé. Répétez L’Étape 3 Si vous le faites.
jetons un coup d’œil à quelques exemples en utilisant ces étapes.
Question 6: Évaluer la limite
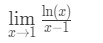
- Étape 1: Évaluation de la limite de directement nous donne
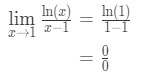
Équation 9: L’hôpital, la règle de la question pt.,2 - Etape 2:
Oui, c’est l’un de la à croissance indéterminée.
- Étape 3:
en appliquant la règle de l’hôpital, nous avons:
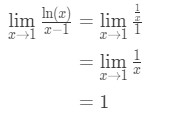
équation 9: la règle de l’hôpital question pt.3 - Étape 4:
on n’est pas une forme indéterminée, donc nous avons terminé et la réponse est 1.
Maintenant que la question était un peu facile, alors pourquoi ne pas nous jeter un oeil à quelque chose qui est un peu plus difficile.,
Question 7: évaluer la limite
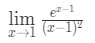
- Étape 1: évaluer la limite directement nous voyons que:
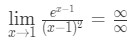
équation 10: la règle de l’hôpital deux fois question pt.2 - Etape 2:
C’est une forme indéterminée, alors passez à l’étape 3.,
- Étape 3:
en appliquant la règle de l’hôpital, nous avons
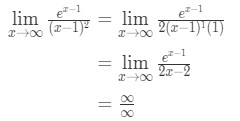
équation 10: la règle de l’hôpital pose deux fois la question pt.3 - Étape 4:
Ceci est une autre forme indéterminée. Nous devons donc revenir à l’étape 3 et appliquer à nouveau les règles de l’hoptial.
- Étape 3:
en appliquant à nouveau la règle de l’Hopital, nous avons:
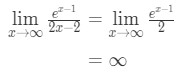
équation 10: la règle de l’Hopital interroge deux fois pt.,4 - Étape 4:
l’Infini n’est pas une forme indéterminée, de sorte que nous sommes fait et la réponse est ∞\infty∞