Es gibt keine einzige Strategie für die Übersetzung von mathematischen Phrasen in algebraische Ausdrücke. Solange Sie sich an die Grundlagen erinnern können, sollten Sie in der Lage sein, die anspruchsvolleren anzugehen. Stellen Sie einfach sicher, dass Sie rechtfertigen können, wie Sie Ihren eigenen algebraischen Ausdruck finden, und was noch wichtiger ist, dass er für Sie sinnvoll ist. Bitten Sie Ihre Lehrer bei Bedarf immer um Hilfe oder arbeiten Sie mit Ihren Klassenkameraden zusammen, damit Sie Ihre Antworten überprüfen können.,
Um Ihre Fähigkeiten beim Schreiben algebraischer Ausdrücke zu erweitern, werden wir verschiedene Möglichkeiten untersuchen, wie jede Operation als Wort oder Phrase im Problem angezeigt werden kann. Die vier arithmetischen Operationen sind Addition, Subtraktion, Multiplikation und Division.,
Key Words for Addition

Key Words for Subtraction

Key Words for Multiplication

Key Words for Division

It is time now time to go over some examples to practice writing algebraic expressions., Ich trenne die Beispiele in zwei:
- Grundlegende Beispiele für algebraische Ausdrücke
- Mehrteilige Beispiele für algebraische Ausdrücke
Grundlegende algebraische Ausdrücke Beispiele
Beispiel 1: Schreiben Sie einen algebraischen Ausdruck für die mathematische Phrase „die Summe einer Zahl und vier“.
Lösung: Das Wort „Summe“ gibt uns sofort den Hinweis, den wir hier hinzufügen werden. Beachten Sie, dass wir zwei Mengen hinzufügen möchten: eine unbekannte Nummer und die Nummer 4. Da wir den Wert der Zahl nicht kennen, können wir sie mit einer Variablen darstellen., Sie können alle Buchstaben des Alphabets verwenden. In diesem Fall stimmen wir der Verwendung von y für die Variable zu.
Wenn wir die Variablen y und 4 hinzufügen, haben wir y + 4. Es ist auch in Ordnung, Ihre Antwort als 4 + y zu schreiben, da die Addition kommutativ ist – das heißt, das Umschalten der Additionsreihenfolge ändert seine Summe nicht.
Die endgültige Antwort ist y+4.
Beispiel 2: Schreiben Sie einen algebraischen Ausdruck für die mathematische Phrase „10 um eine Zahl erhöht“.
Lösung: Die Schlüsselwörter „erhöht durch“ implizieren Addition. Dies bedeutet, dass eine unbekannte Zahl zu 10 hinzugefügt wurde., Mit dem Buchstaben k als Variable können wir die obige Anweisung als 10 + k übersetzen. Da Addition kommutativ ist, können wir sie als k + 10 umschreiben. Eine der beiden oben genannten ist eine richtige Antwort.
Die endgültige Antwort ist k+10.
Beispiel 3: Schreiben Sie einen algebraischen Ausdruck für die mathematische Phrase“die Differenz von 1 und einer Zahl“.
Lösung: Das Wort „Unterschied“ deutet darauf hin, dass wir subtrahieren werden. Wenn Sie auf dieses mathematische Wort (Unterschied) stoßen, achten Sie außerdem auf die Reihenfolge. Die Nummer 1 kommt zuerst, dann kommt eine unbekannte Nummer an zweiter Stelle., Das bedeutet, dass die Zahl 1 der Minuend und die unbekannte Zahl der Subtrahend ist. Wenn wir uns entscheiden, den Buchstaben x als Variable zu verwenden, wird die Antwort 1-x.
Die endgültige Antwort ist 1-x.
Beispiel 4: Schreiben Sie einen algebraischen Ausdruck für die mathematische Phrase „eine Zahl kleiner als 8“.
Lösung: Seien Sie sehr vorsichtig beim Umgang mit den Schlüsselwörtern „less than“. Die erste Menge, die vor den Schlüsselwörtern „kleiner als“ steht, die „eine Zahl“ ist, ist der Subtrahend. Während die Menge, die danach kommt, zum Minuend wird.,
Mit anderen Worten, wir werden die unbekannte Zahl von der Zahl 8 subtrahieren. Wenn wir unsere Variable als Buchstaben a auswählen, erhalten wir 8-a.
Die endgültige Antwort lautet 8-a.
Beispiel 5: Schreiben Sie einen algebraischen Ausdruck für die mathematische Phrase „das Produkt aus 5 und einer Zahl“.
Lösung: Um das Produkt aus zwei Größen oder Werten zu finden, bedeutet dies, dass wir sie zusammen multiplizieren. Wenn wir den Buchstaben m als unsere Variable auswählen, ist der algebraische Ausdruck für diese mathematische Phrase einfach 5m. Es bedeutet 5 mal die unbekannte Zahl m.
Die endgültige Antwort ist 5m.,
Beispiel 6: Schreiben Sie einen algebraischen Ausdruck für die mathematische Phrase „zweimal eine Zahl“.
Lösung: Das Wort „zweimal“ bedeutet, dass wir etwas verdoppeln werden. In diesem Fall möchten wir einen unbekannten Wert oder eine unbekannte Menge verdoppeln. Sei der Buchstabe d die unbekannte Zahl, wenn wir sie verdoppeln, erhalten wir den algebraischen Ausdruck 2d.
Die endgültige Antwort ist 2d.
Beispiel 7: Schreiben Sie einen algebraischen Ausdruck für die mathematische Phrase „der Quotient einer Zahl und 7“.
Lösung: Das Schlüsselwort „Quotient“ bedeutet, dass wir die Operation der Division durchführen. Wir werden eine unbekannte Zahl durch 7 teilen., Wenn Sie den Buchstaben w als Variable auswählen, kann die obige mathematische Phrase als algebraischer Ausdruck unten ausgedrückt werden.
,\LARGE{w \over 7}
Beispiel 8: Schreiben Sie einen algebraischen Ausdruck für die mathematische Formulierung „das Verhältnis von 10 und einer Zahl“.
Lösung: In ähnlicher Weise bedeutet das Wort „Verhältnis“ Division. Die Reihenfolge hier ist sehr wichtig. Die erste Menge ist die Zahl 10 und die zweite Menge ist die unbekannte Zahl. Das bedeutet, dass 10 durch eine unbekannte Zahl geteilt wird., Sei c die unbekannte Zahl, der algebraische Ausdruck für die obige mathematische Phrase kann als
\LARGE{10 \over c}
Mehrteilige algebraische Ausdrücke geschrieben werden Beispiele
Dieses Mal werden wir uns mit mathematischen Phrasen befassen, die etwas komplexer sind. Die algebraischen Ausdrücke können hier zwei oder mehr Operationen enthalten. Die grundlegenden Schlüsselwörter, die wir zuvor gelernt haben, dienen als Grundlage für die Arbeit mit den anspruchsvolleren mathematischen Phrasen, die wir in algebraische Ausdrücke interpretieren können.,
Beispiel 1: Schreiben Sie einen algebraischen Ausdruck für die mathematische Phrase“3 mehr als zweimal eine Zahl“.
Lösung: Um dies viel einfacher zu verstehen, werden wir diesen Satz in zwei Teile unterteilen. Erkenne zuerst, dass wir eine unbekannte Nummer haben. Wir können es durch beliebige Buchstaben des Alphabets darstellen. Sei die unbekannte Zahl die Variable x. Das folgende Diagramm sollte uns helfen zu sehen, was wirklich los ist.,
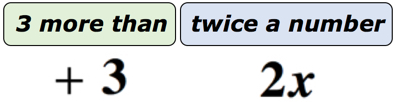
Wenn Sie darüber nachdenken, gibt es eine unbekannte Zahl, die durch die Variable x dargestellt wird, die verdoppelt oder mit 2 multipliziert wird. Was auch immer das Produkt ist, wir werden 3 hinzufügen. Unsere endgültige Antwort sollte also wie die folgende aussehen.
Die endgültige Antwort ist 2x+3.
Beispiel 2: Schreiben Sie einen algebraischen Ausdruck für die mathematische Phrase“die Differenz einer halben Zahl und 10″.
Lösung: Angenommen, die Variable y ist die unbekannte Zahl., Das Schlüsselwort „Unterschied“ fordert uns auf, eine Subtraktion durchzuführen. Hier ist es entscheidend, dass wir auf die Reihenfolge der Subtraktion achten. Nach dem Wort „Unterschied“ sollten wir zwei Mengen erwarten. Der erste wird der Minuend sein, während der zweite der Subtrahend sein wird. Schauen Sie sich das Diagramm unten an.
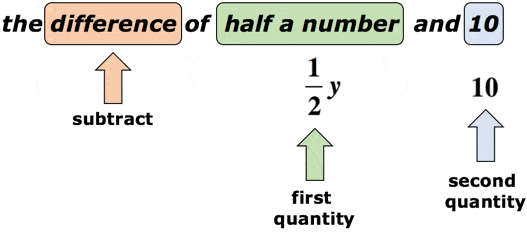
In Bezug auf das obige Diagramm subtrahieren wir die erste Menge um die zweite Menge. Mit anderen Worten, die zweite Menge wird von der ersten Menge subtrahiert., Die endgültige Antwort für mathematische Phrase sollte so etwas wie diese,
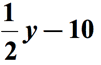
Beispiel 3: Schreiben Sie einen algebraischen Ausdruck für die mathematische Phrase“7 weniger als das Produkt einer Zahl und 6″.
Lösung: Wir wissen, dass „less than“ eine Subtraktionsoperation vorschlägt. Aber wir müssen hier ein bisschen vorsichtig sein, weil die Reihenfolge, wie wir subtrahieren, wichtig ist. Angenommen, die unbekannte Zahl wird durch die Variable k dargestellt. Setzen wir dies in ein Diagramm, um einen Sinn dafür zu machen.,
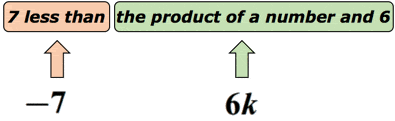
Tatsächlich kann diese mathematische Phrase als
“ das Produkt einer Zahl und 6 minus 7 „
umgeschrieben werden Die „7 kleiner als“ bedeutet „minus 7“ zu welcher Menge auch immer beschrieben wird, was in diesem Fall „das Produkt einer Zahl und 6“. Hier ist die endgültige Interpretation der mathematischen Phrase in einem algebraischen Ausdruck:
6k-7
Beispiel 4: Schreiben Sie einen algebraischen Ausdruck für die mathematische Phrase „der Durchschnitt einer Zahl und 4“.,
Lösung: Um mit dieser speziellen mathematischen Phrase zu beginnen, müssen wir überprüfen, was das Wort „Durchschnitt“ bedeutet. Um den Durchschnitt oder Mittelwert von zwei oder mehr Zahlen zu berechnen, müssen wir alle Zahlen addieren, um eine Summe zu erhalten, und sie dann durch die Anzahl der Einträge oder die Anzahl der Zahlen dividieren. Wenn wir m die Variable zur Darstellung der unbekannten Zahl lassen, kann die obige mathematische Phrase in algebraischen Ausdrücken ausgedrückt werden als
\LARGE{{m + 4} \over 2}
Beispiel 5: Schreiben Sie einen algebraischen Ausdruck für die mathematische Phrase „der Quotient von 1 und 1 um eine Zahl verringert“.,
Lösung: Das Schlüsselwort „Quotient“ bedeutet, dass wir teilen werden. In diesem Fall möchten wir die Zahl 1 durch die Menge 1 dividieren, die um eine Zahl verringert wurde. Unten ist der algebraische Ausdruck, der die mathematische Phrase oben darstellen kann. Sei a die unbekannte Nummer.
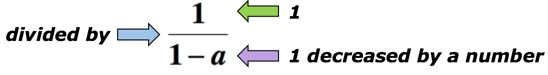
Beispiel 6: Schreiben Sie einen algebraischen Ausdruck für die mathematische Phrase“ein Drittel des Quadrats einer Zahl, erhöht um 2″.
Lösung: Hier ist einiges los., Erstens kann der Teil der Phrase, der „ein Drittel des Quadrats einer Zahl“ angibt, als “ das Quadrat einer Zahl geteilt durch 3 „interpretiert werden. Wir müssen die unbekannte Zahl um 2 erhöhen und dann durch 3 teilen. Angenommen, der unbekannte Anzahl von t erhalten wir
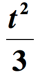
Wir sind noch nicht fertig. Der letzte Schritt besteht darin, die obige Menge um 2 hinzuzufügen, um den verbleibenden Teil des Ausdrucks “ um 2 erhöht „zu integrieren. Also hier ist die endgültige Darstellung der gegebenen mathematischen Phrase.,
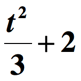
You might also be interested in:
Algebraic Expressions
Algebraic Sentences Word Problems