linjär Approximation
låt oss säga att en dag du glömde en kalkylator och du verkligen vill hitta hur vad kvadratroten av 2 är. Hur skulle vi ta reda på det utan en miniräknare? Vi kan använda linjär approximation!
Linearisering av en funktion
lineariseringen av en funktion handlar bara om att hitta tangentlinjen för funktionen vid en viss punkt på ett annat sätt., Lineariseringsformeln är:

där L(x) är ekvationen för tangentlinjen vid punkt a.
hur är det användbart för oss? Tja, vi kan faktiskt använda denna ekvation för att approximera värdena för funktionen nära punkt a. ta en titt på den här grafen.,
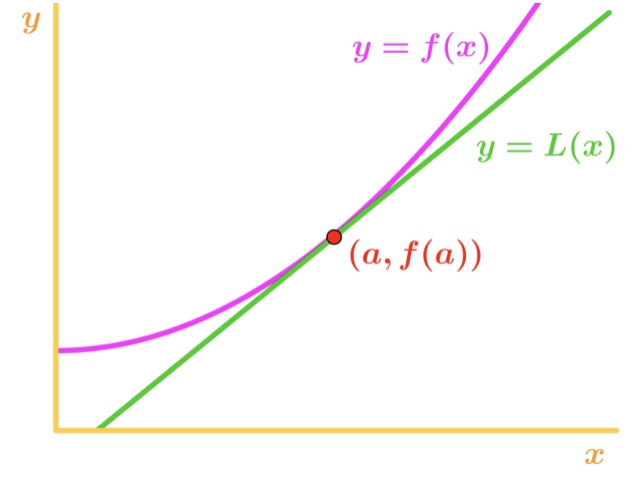
Observera att för x-värden nära punkt a ser vi att funktionen och tangentlinjen är relativt nära varandra. På grund av detta kan vi skriva att funktionen är ungefär lika med tangentlinjen nära punkt a., Med andra ord,

där\CA är den ungefärliga symbolen. Denna ekvation kallas linjär approximation formel. Det är linjärt i en mening att tangenten är en rak linje och vi använder den för att approximera funktionen. Med hjälp av denna approximation kan vi approximera värden som inte kan göras för hand. Till exempel kan kvadratroten av 2 eller den naturliga loggen på 5 alla approximeras!, En viktig sak att notera är att denna approximation bara fungerar för x-värden nära punkt a. om du har ett X-värde långt ifrån punkt A, blir approximationen verkligen felaktig.
nu tar vi inte en titt på några exempel på att hitta lineariseringen av en funktion och sedan titta på hur man använder linjär approximation!
hitta lineariseringen av L (x) av funktionen vid en
Fråga 1: överväga funktionen
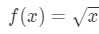
låt oss säga att vi vill hitta linjäriseringen av funktionen vid punkt a=4.
för att hitta lineariseringen L(x), kom ihåg att

- Steg 1: Hitta en
- steg 2: Hitta f(a)
- steg 3: Hitta f'(a).
- steg 4: Anslut alla tre till formeln för att hitta L (x)
-
låt oss följa dessa steg!,
Steg 1: lyckligtvis a = 4 ges till oss i frågan, Så vi behöver inte leta efter det.
- steg 2:
Lägg märke till att
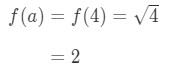
ekvation 1: Lineariseringsfråga pt. 3 - steg 3:
vet att derivatet av kvadratiska rötter är
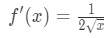
ekvation 1: Lineariseringsfråga pt., 4 And so plugging in x=a gives us:
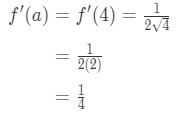
Equation 1: Linearization question pt. 5 - Step 4:
Since we know a, f(a), and f'(a), we can now plug it into L(x) to find the linearization of f(x).
Hence,
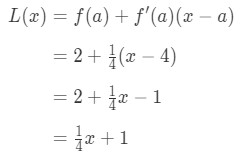
Equation 1: Linearization question pt., 6 Så L(x)=14\frac{1}{4}41x+1 är lineariseringen av denna funktion vid punkt x=4. Dessutom är det också tangentlinjen för funktionen vid punkt x=4.
hur man gör linjär approximation
Kom ihåg tidigare vi sa att vi kunde använda ekvationen för tangentlinjen för att approximera värdena för funktionen nära en? Låt oss prova det här med lineariseringen vi hittade tidigare. Minns att
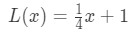
för punkter nära x=4. Vi kan ändra detta till en linjär approximation för f(x) genom att säga att:
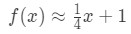
låt oss säga att jag vill approximera f(4.04). Om du skulle ansluta detta till den ursprungliga funktionen skulle du få 4.04 \ sqrt{4.04}4.04 . Detta skulle vara riktigt svårt att beräkna utan en miniräknare., Men med hjälp av linjär approximation kan vi säga att

hittills har dessa frågor gett oss en funktion och en punkt att arbeta med. Tänk om inget av dessa gavs alls? Vad händer om frågan bara säger oss att uppskatta ett nummer?
använd linjär approximation för att uppskatta ett tal
Antag att vi vill uppskatta 10\sqrt{10}10. Hur skulle vi göra det?, Vi skulle behöva använda den linjära approximationen

men vi har inte ens en funktion och en punkt att arbeta med. Det betyder att vi måste göra dem själva. Detta leder oss till att göra följande steg:
- Steg 1: Skapa en funktion
- steg 2: Skapa punkt a
- steg 3: Hitta f (A) och f'(a)
- steg 4: Anslut allt till linjär approximation formel
låt oss följa stegen!,
fråga 2: uppskattning 10\sqrt{10}10
- Steg 1: Låt oss komma med en funktion. Observera att vi uppskattar
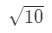
ekvation 3: uppskattning med linjär ca. pt.2 vi måste på något sätt göra ett förhållande mellan f(x) och 10\sqrt{10}10. Vi kan inte säga att f (x) = 10\sqrt{10}10 eftersom funktionen inte kommer att vara beroende av x. så varför gör vi inte det här? Låt
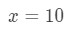
ekvation 3: uppskattning med linjär ca. pt.,3 om vi gör det säger vi i grunden
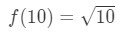
ekvation 3: uppskattning med linjär ca. pt.4 vi kan nu självklart berätta vad funktionen ska vara. Låt
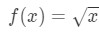
ekvation 3: uppskattning med linjär ca. pt.5 så vi har en funktion, men nu behöver vi en punkt A att arbeta med.,
- steg 2:
nyckeln till att hitta rätt värde a är genom att överväga två saker:
1) Se till att värdet A ligger nära x
2) Se till att f(a) är ett fint nummer.
skulle a = 8 vara tillräckligt? Tja, 8 är ganska nära 10 så det är inte dåligt.
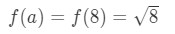
ekvation 3: uppskattning med linjär ca. pt.6 Observera att 8\sqrt{8}8 inte är ett mycket trevligt nummer. Faktum är att du får en massa decimaler. Så vi måste prova något annat.,
skulle a = 9 vara tillräckligt? Återigen är 9 ganska nära 10 så det är okej. Dessutom

ekvation 3: uppskattning med linjär ca. pt.7 f(a) är faktiskt ett fint heltal här, så det fungerar faktiskt! Så att plocka a = 9 är tillräckligt.
- steg 3:
notera att från tidigare:

ekvation 3: uppskattning med linjär ca. pt.,8 Calculating f'(x) we have again:

Equation 3: Estimate with linear approx. pt.9 So
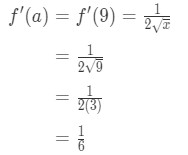
Equation 3: Estimate with linear approx. pt.,10 - Step 4:
Going back to the linear approximation formula we have:

Equation 3: Estimate with linear approx. pt.11 Plugging a, f(a), f'(a), f(x), and x in our formula you will see that:

Equation 3: Estimate with linear approx. pt.12 Hence, we just approximated the number!,
om du vill ha mer övningsproblem om linjär approximation, rekommenderar jag att du tittar på den här länken här.
http://tutorial.math.lamar.edu/Classes/CalcI/LinearApproximations.aspx
överskattar och underskattar
vi vet att linjär approximation bara är en uppskattning av funktionens värde vid en viss punkt. Men hur vet vi att om vår uppskattning är en överskattning eller en underskattning? Vi beräknar det andra derivatet och tittar på konkaviteten.,
konkav upp mot konkav ner
om det andra derivatet av funktionen är större än 0 för värden nära A, är funktionen konkav upp. Detta innebär att vår approximation kommer att bli en underskattning. Med andra ord,
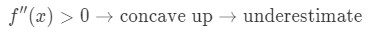
varför? Låt oss ta en titt på den här grafen.,
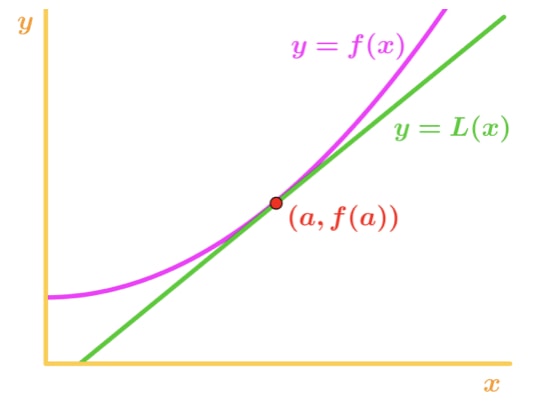
Observera att f(x) är konkav uppåt och tangentlinjen är rätt under f(x). Låt oss säga att använda tangentlinjen för att approximera f (x). Då kommer Y-värdena för tangentlinjen alltid att vara mindre än det faktiska värdet av f(x). Därför har vi en underskattning
Nu om det andra derivatet av funktionen är mindre än 0 för värden nära A, är funktionen konkav ner., Detta innebär att vår approximation kommer att bli en överskattning. Med andra ord,
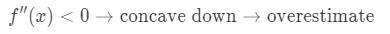
igen, varför? Låt oss ta en titt på ett annat diagram.
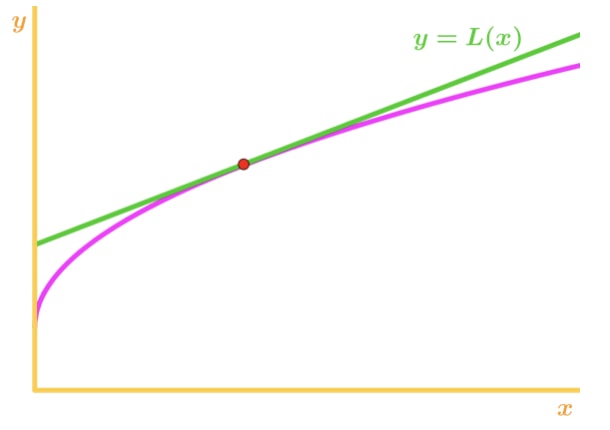
Lägg märke till att f(x) är konkav nedåt och tangentlinjen ligger precis ovanför f(x). Återigen, låt oss säga att vi kommer att använda tangentlinjen för att approximera f (x)., Då kommer Y-värdena för tangentlinjen alltid att vara större än det faktiska värdet av f(x). Därför har vi en överskattning.
Så om du någonsin behöver se om ditt värde är en underskattning eller en överskattning, se till att du följer dessa steg:
- Steg 1: Hitta det andra derivatet
- steg 2: titta på konkaviteten hos funktionen nära punkt a
- steg 3: Bekräfta att det är en underskattning/överskattning
låt oss ta en titt på ett exempel:
fråga 3: Låt f(x) = x\sqrt{x}x och A = 4. Om vi linjära ungefärliga f (4.,04), skulle det vara en överskattning eller en underskattning?
- Steg 1: Se till att
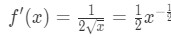
ekvation 4: överskattad fråga pt.1 så det andra derivatet är
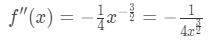
ekvation 4: överskattad fråga pt.2 - steg 2:
Observera att a=4, Så vi vill titta på positiva värden på x nära 4. Titta nu på det andra derivatet., När x är positivt ser vi att
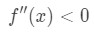
ekvation 4: överskattar frågan pt.3 det är därför konkavt ner
- steg 3:
vi vet att om funktionen är konkav ner, kommer tangentlinjen att ligga över funktionen. Därför kommer användningen av tangentlinjen som en approximation att ge ett överskattat värde.
skillnader
inte bara kan vi approximera värden med linjär approximation, men vi kan också approximera med skillnader., För att approximera använder vi följande formel
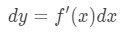
där dy och dx är differentialer, och f'(x) är derivatet av f när det gäller x. eftersom vi har att göra med mycket små förändringar i x och Y, då kommer vi att använda det faktum att:
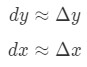
de flesta av de frågor vi ställer in
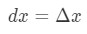
så att använda dessa fakta kommer att leda oss att ha:
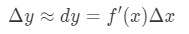
denna approximation är mycket användbar när man approximerar förändringen av y., Tänk på då hade de inte räknare, så det här är den bästa approximationen de kunde få för funktioner med kvadratiska rötter eller naturliga stockar.
För det mesta måste du leta efter f'(x) och Δ\DeltaΔx själv. Med andra ord, följ dessa steg för att approximera Δ\DeltaΔy!
- Steg 1: Hitta Δ\DeltaΔx
- steg 2: Hitta f'(x)
- steg 3: Anslut allt till formeln för att hitta dy. dy kommer att vara approximationen för Δ \ DeltaΔy.
låt oss titta på ett exempel på att använda denna approximation:
fråga 4: överväga funktionen y = ln (x + 1)., Antag att X ändras från 0 till 0,01. Ungefärliga Δ\DeltaΔy.
- Steg 1: Lägg märke till att x ändras från 0 till 0,01, så förändringen i x skulle vara:
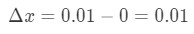
ekvation 6: Differentialfråga pt.1 - steg 2:
derivatet skulle vara:
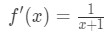
ekvation 6: Differentialfråga pt.,2 - steg 3:
koppla in allt vi har:
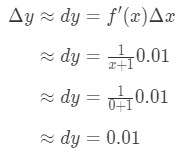
ekvation 6: Differentialfråga pt.3 därav, Δ \ DeltaΔy \ca 0,01
men för det mesta vill vi uppskatta ett värde av funktionen, och inte förändringen av värdet. Därför lägger vi till båda sidor av ekvationen med y, vilket ger oss:
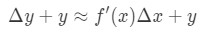
vilket är detsamma som:
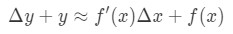
denna ekvation är lite svår att läsa, Så vi kommer att omorganisera den ännu mer. Låt oss försöka bli av med y Och Δ \ DeltaΔy. Observera att Δ\DeltaΔy+y i grunden är detsamma som att hitta värdet på funktionen vid Δ\DeltaΔx + x. med andra ord,
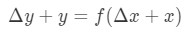
därmed ersätta detta i vår approximation ovan kommer att ge oss:
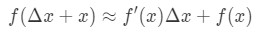
där F(Δ\DeltaΔx+x) är värde som vi försöker uppskatta. Hur använder vi denna formel? Jag rekommenderar att du följer dessa steg:
låt oss använda dessa steg för följande fråga.
fråga 5: använd skillnader för att approximera 10 \ sqrt{10}10.
- Steg 1: Jämför f(Δ\DeltaΔx+x) med 10\sqrt{10}10., Since 10\sqrt{10}10 has a square root and 9 is a perfect square that is closest to 10, then let
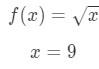
Equation 7: Approximate value with differentials pt.1 Notice that:
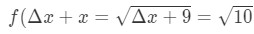
Equation 7: Approximate value with differentials pt.,2 se till att det inte finns något annat val än att låta Δ\DeltaΔx = 1
- steg 2:
se till att derivatet ger:

ekvation 7: ungefärligt värde med skillnader pt.3 så detta innebär
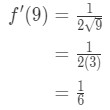
ekvation 7: ungefärligt värde med skillnader pt.,4 - steg 3:
koppla in allt i formeln ger oss:
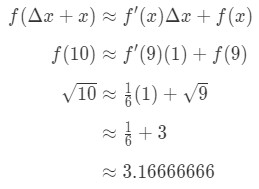
ekvation 7: ungefärligt värde med differentialer pt.5 därför approximerade vi bara numret.
en intressant sak att notera är att linjär approximation och differentialer båda ger samma resultat för 10 \ sqrt{10}10.,
om du vill veta mer om skillnader klickar du på den här länken:
http://tutorial.math.lamar.edu/Classes/CalcI/LinearApproximations.aspx
bevisar l ’ Hospitals regel med linjär approximation
nu har vi lärt oss mycket om linjär approximation, men vad kan vi göra med det? Vi kan faktiskt använda linjär approximation formel för att bevisa en regel som kallas L ’ Hospitals regel . Så här fungerar beviset.
minns att den linjära approximationsformeln är:

se till att vi kan ordna om formeln så att:
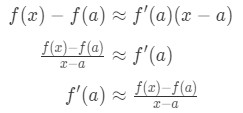
inser att approximationen blir mer och mer exakt när vi väljer x-värden som ligger närmare en. med andra ord om vi tar gränsen som x→A, så kommer de att vara lika. Så
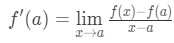
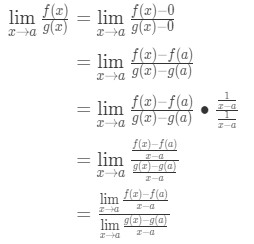
lägg nu märke till att vi kan tillämpa formeln som vi härledde tidigare här. Så nu
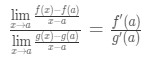
nu istället för att skriva f'(A) och g'(a), kan vi tillämpa gränser som x→A (eftersom vi vet f och g är differentierbara)., Så
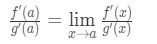
därför visade vi bara att:
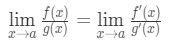
vilken är l ’ hospitals regel .
när du ska använda L ’hopitals regel
vi vill alltid tillämpa l’ hoptials regel när vi stöter på obestämda gränser. Det finns två typer av obestämda former., Dessa obestämda former skulle vara:
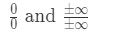
många människor gör misstaget att använda L ’ hopitals regel utan att ens kontrollera om det är en obestämd gräns. Så se till att du kolla det först! Annars kommer det inte att fungera och du kommer att få fel svar. Här är en guide till att använda L ’ hopitals regel:
- Steg 1: Utvärdera gränsen direkt.
- steg 2: Kontrollera om det är en av de obestämda formerna. Om det är, gå till steg 3.,
- steg 3: Använd l ’ hopitals regel.
- steg 4: Kontrollera om du får en annan obestämd form. Upprepa steg 3 Om du gör det.
Låt oss ta en titt på några exempel med hjälp av dessa steg.
Fråga 6: utvärdera gränsen
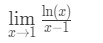
- Steg 1: utvärdering av gränsen ger oss direkt
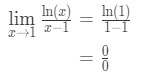
ekvation 9: l ’ hopitals regelfråga pt.,2 - steg 2:
Ja, det är en av de obestämda formerna.
- steg 3:
tillämpa l ’ hopitals regel vi har:
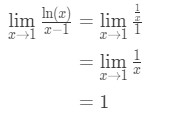
ekvation 9: l ’ hopitals regelfråga pt.3 - steg 4:
en är inte en obestämd form, så vi är klara och svaret är 1.
Nu var den frågan lite lätt, så varför tar vi inte en titt på något som är lite svårare.,
Fråga 7: utvärdera gränsen
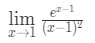
- Steg 1: Utvärdera gränsen direkt vi ser att:
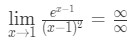
ekvation 10: l ’ hopitals regel två gånger fråga pt.2 - steg 2:
detta är en obestämd form, så gå till steg 3.,
- steg 3:
tillämpa l ’ hopitals regel vi har
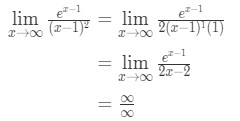
ekvation 10: l ’ hopitals regel två gånger fråga pt.3 - steg 4:
detta är en annan obestämd form. Så vi måste gå tillbaka till steg 3 och tillämpa l ’ hoptials regler igen.
- steg 3:
tillämpa l ’ hopitals regel igen vi har:
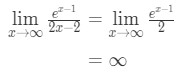
ekvation 10: l ’ hopitals regel två gånger fråga pt.,4 - steg 4:
Infinity är inte en obestämd form, så vi är klara och svaret är \ infty