Aproksymacja liniowa
powiedzmy, że pewnego dnia zapomniałeś o kalkulatorze i naprawdę chcesz dowiedzieć się, jak jest pierwiastek kwadratowy z 2. Jak byśmy się dowiedzieli bez kalkulatora? Możemy użyć aproksymacji liniowej!
linearyzacja funkcji
linearyzacja funkcji polega na znalezieniu linii stycznej funkcji w określonym punkcie w inny sposób., Wzór linearyzacji to:

gdzie L(x) jest równaniem linii stycznej w punkcie a.
w jaki sposób jest to dla nas przydatne? Możemy użyć tego równania do przybliżenia wartości funkcji w pobliżu punktu A. spójrz na ten wykres.,
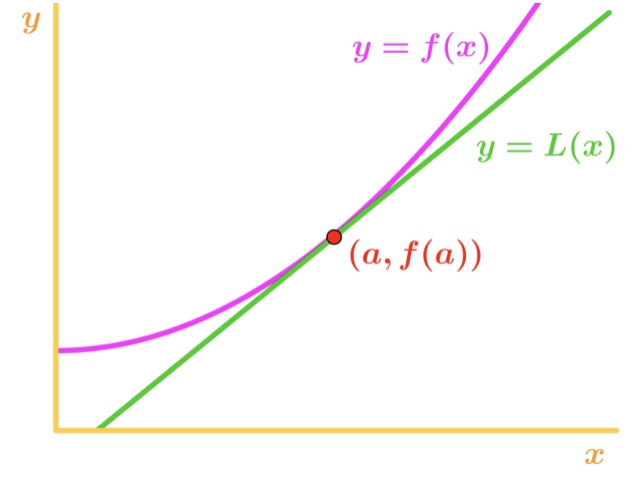
zauważ, że dla wartości x w pobliżu punktu a widzimy, że funkcja i linia styczna stosunkowo blisko siebie. Z tego powodu możemy napisać, że funkcja jest w przybliżeniu równa linii stycznej w pobliżu punktu A., Innymi słowy,

gdzie ≈\approx≈ jest symbolem w przybliżeniu. Równanie to znane jest jako wzór aproksymacji liniowej. Jest liniowa w tym sensie, że styczna jest linią prostą i używamy jej do przybliżenia funkcji. Korzystając z tego przybliżenia, jesteśmy w stanie przybliżać wartości, których nie można wykonać ręcznie. Na przykład pierwiastek kwadratowy z 2 lub log naturalny z 5 mogą być przybliżone!, Jedną ważną rzeczą jest to, że to przybliżenie działa tylko dla wartości x w pobliżu punktu a. jeśli masz wartość x daleko od punktu a, to przybliżenie staje się naprawdę niedokładne.
teraz przyjrzyjmy się kilku przykładom znajdowania linearyzacji funkcji, a następnie przyjrzyjmy się, jak używać aproksymacji liniowej!
Znajdź linearyzację L(x) funkcji w
Pytanie 1: rozważmy funkcję
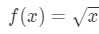
powiedzmy, że chcemy znaleźć linearyzację funkcji w punkcie a=4.
aby znaleźć linearyzację L(x), przypomnij sobie, że

- Krok 1: Znajdź a
- Krok 2: Znajdź f(a)
- Krok 3: Znajdź f'(a).
- Krok 4: Podłącz wszystkie trzy do formuły, aby znaleźć L (x)
-
wykonajmy te kroki!,
Krok 1: Na szczęście w pytaniu podano nam a = 4, więc nie musimy go szukać.
- Krok 2:
zauważ, że
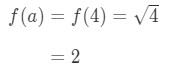
równanie 1: Pytanie o linearyzację pt. 3 - Krok 3:
wiedzieć, że pochodna pierwiastków kwadratowych jest
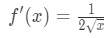
równanie 1: Pytanie o linearyzację pt., 4 And so plugging in x=a gives us:
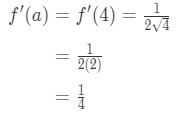
Equation 1: Linearization question pt. 5 - Step 4:
Since we know a, f(a), and f'(a), we can now plug it into L(x) to find the linearization of f(x).
Hence,
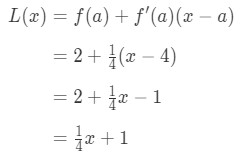
Equation 1: Linearization question pt., 6 Tak więc L(x)=14\frac{1}{4} 41x+1 jest linearyzacją tej funkcji w punkcie x=4. Ponadto jest to również linia styczna funkcji w punkcie x=4.
jak zrobić aproksymację liniową
pamiętaj, że wcześniej mówiliśmy, że możemy użyć równania linii stycznej do przybliżenia wartości funkcji w pobliżu a? Spróbujmy z linearyzacją, którą znaleźliśmy wcześniej. Przypomnijmy, że
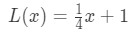
dla punktów w pobliżu x=4. Możemy to zmienić w aproksymację liniową dla f (x) mówiąc, że:
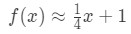
teraz powiedzmy, że chcę przybliżać f(4.04). Jeśli podłączysz to do oryginalnej funkcji, otrzymasz 4.04\sqrt{4.04}4.04 . Byłoby to naprawdę trudne do obliczenia bez kalkulatora., Jednak, używając aproksymacji liniowej, możemy powiedzieć, że

jak dotąd te pytania dały nam funkcję i punkt do pracy. Co, jeśli nic z nich nie zostało podane? Co jeśli pytanie mówi nam tylko, aby oszacować liczbę?
użyj aproksymacji liniowej, aby oszacować liczbę
Załóżmy, że chcemy oszacować 10\sqrt{10}10. Jak to zrobimy?, Będziemy musieli użyć aproksymacji liniowej

ale nie mamy nawet funkcji i punktu do pracy. To oznacza, że musimy je zrobić sami. To prowadzi nas do następujących kroków:
- Krok 1: Utwórz funkcję
- Krok 2: Utwórz punkt a
- Krok 3: Znajdź f(a) i f'(a)
- Krok 4: Podłącz wszystko do liniowej formuły aproksymacji
wykonajmy kroki!,
Pytanie 2: oszacuj 10\sqrt{10}10
- Krok 1: wymyślmy funkcję. Zauważ, że szacujemy
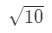
równanie 3: szacujemy z liniowym ok. pt.2 musimy jakoś stworzyć zależność między f (x) i 10\sqrt{10} 10. Nie możemy powiedzieć, że f (x) = 10\sqrt{10}10, ponieważ funkcja nie będzie zależna od x. więc dlaczego tego nie zrobimy? Niech
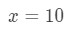
równanie 3: oszacowanie z liniowym ok. pt.,3 jeśli to zrobimy, to zasadniczo mówimy
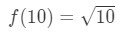
równanie 3: oszacowanie z liniowym ok. pt.4 możemy teraz oczywiście powiedzieć, jaka powinna być funkcja. Niech
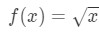
równanie 3: oszacowanie z liniowym ok. pt.5 mamy więc funkcję, ale teraz potrzebujemy punktu a do pracy.,
- Krok 2:
kluczem do znalezienia odpowiedniej wartości a jest rozważenie dwóch rzeczy:
1) Upewnij się, że wartość a jest bliska x
2) Upewnij się, że f(a) jest ładną liczbą.
Czy a = 8 wystarczy? 8 jest blisko 10, więc nie jest źle. Jednak
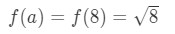
równanie 3: oszacowanie z liniowym ok. pt.6 zauważ, że 8\sqrt{8}8 nie jest zbyt ładną liczbą. W rzeczywistości, dostajesz kilka liczb dziesiętnych. Więc musimy spróbować czegoś innego.,
Czy a = 9 wystarczy? Ponownie, 9 jest dość blisko 10 więc jest w porządku. Ponadto

równanie 3: oszacowanie z liniowym ok. pt.7 f (a) jest w rzeczywistości ładną liczbą całkowitą, więc to naprawdę działa! Więc wybranie a = 9 jest wystarczające.
- Krok 3:
zauważ, że od początku:

równanie 3: oszacuj z liniowym ok. pt.,8 Calculating f'(x) we have again:

Equation 3: Estimate with linear approx. pt.9 So
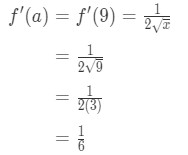
Equation 3: Estimate with linear approx. pt.,10 - Step 4:
Going back to the linear approximation formula we have:

Equation 3: Estimate with linear approx. pt.11 Plugging a, f(a), f'(a), f(x), and x in our formula you will see that:

Equation 3: Estimate with linear approx. pt.12 Hence, we just approximated the number!,
Jeśli chcesz mieć więcej problemów z przybliżeniem liniowym, to polecam zajrzeć na ten link tutaj.
http://tutorial.math.lamar.edu/Classes/CalcI/LinearApproximations.aspx
przeceniaj i Niedoceniaj
wiemy, że aproksymacja liniowa jest tylko estymacją wartości funkcji w określonym punkcie. Skąd jednak wiemy, że jeśli nasza ocena jest przeszacowana lub niedoceniana? Obliczamy drugą pochodną i przyglądamy się wklęsłości.,
Wklęsła w górę vs Wklęsła w dół
jeśli druga pochodna funkcji jest większa niż 0 dla wartości w pobliżu a, to funkcja jest wklęsła w górę. Oznacza to, że nasze zbliżenie będzie niedoszacowane. Innymi słowy,
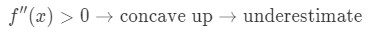
Dlaczego? Spójrzmy na ten wykres.,
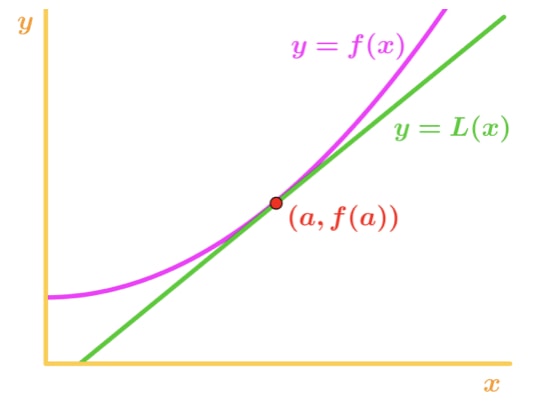
zauważ, że f(x) jest wklęsła do góry, a linia styczna jest tuż pod f(x). Załóżmy, że użyjemy linii stycznej do przybliżenia f (x). Wtedy wartości y linii stycznej zawsze będą mniejsze od rzeczywistej wartości f (x). Stąd mamy teraz
jeśli druga pochodna funkcji jest mniejsza niż 0 dla wartości bliskich a, to funkcja jest wklęsła w dół., Oznacza to, że nasze przybliżenie będzie przeszacowaniem. Innymi słowy,
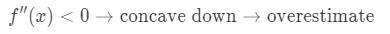
ponownie, dlaczego? Spójrzmy na inny wykres.
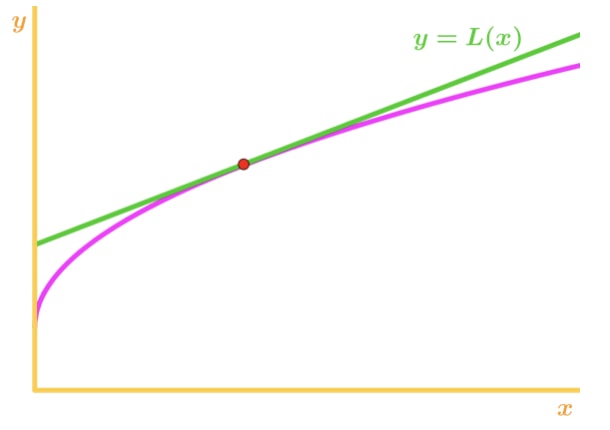
zauważ, że f(x) jest wklęsła w dół, a linia styczna jest tuż nad f (x). X). Ponownie, powiedzmy, że użyjemy linii stycznej do przybliżenia f (x)., Wtedy wartości y linii stycznej zawsze będą większe niż rzeczywista wartość f (x). Stąd mamy przeszacowanie.
więc jeśli kiedykolwiek chcesz zobaczyć, czy Twoja wartość jest niedoszacowaniem lub przeszacowaniem, upewnij się, że wykonasz następujące kroki:
- Krok 1: Znajdź drugą pochodną
- Krok 2: przyjrzyj się wklęsłości funkcji w pobliżu punktu a
- Krok 3: potwierdź, że jest to niedoszacowanie/przeszacowanie
przyjrzyjmy się przykładowi:
pytanie 3: pozwól, X) = X\sqrt{x}X oraz A = 4. Jeśli liniowo przybliżamy f (4.,04), czy byłoby to przeszacowanie czy niedocenianie?
- Krok 1: zobacz, że
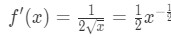
równanie 4: przecenić pytanie pt.1 więc druga pochodna to
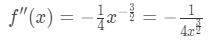
równanie 4: przecenić pytanie pt.2 - Krok 2:
zauważ, że a=4, więc chcemy spojrzeć na dodatnie wartości X w pobliżu 4. Teraz spójrz na drugą pochodną., Gdy X jest dodatnie, widzimy, że
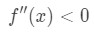
równanie 4: przecenić pytanie pt.3 dlatego jest ona wklęsła w dół
- Krok 3:
wiemy, że jeśli funkcja jest wklęsła w dół, to linia styczna będzie powyżej funkcji. Stąd użycie linii stycznej jako aproksymacji da przeszacowaną wartość.
różnice
możemy nie tylko przybliżać wartości za pomocą aproksymacji liniowej, ale także przybliżać za pomocą różnic., Dla przybliżenia, używamy następującego wzoru
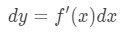
gdzie dy i dx są różnicami, A f'(x) to pochodna F w kategoriach x. ponieważ mamy do czynienia z bardzo małymi zmianami w X i y, będziemy używać faktu, że:
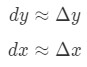
jednak większość pytań dotyczy ustawienia
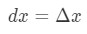
więc korzystanie z tych faktów doprowadzi nas do:
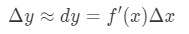
to przybliżenie jest bardzo przydatne przy przybliżaniu zmiany y., Pamiętaj, że wtedy nie mieli kalkulatorów, więc jest to najlepsze przybliżenie, jakie mogli uzyskać dla funkcji z korzeniami kwadratowymi lub naturalnymi logami.
przez większość czasu będziesz musiał sam szukać f'(x) i Δ\DeltaΔx. Innymi słowy, wykonaj te kroki, aby zbliżyć Δ\DeltaΔy!
- Krok 1: Znajdź Δ\DeltaΔx
- Krok 2: Znajdź f'(X)
- Krok 3: Podłącz wszystko do formuły, aby znaleźć dy. dy będzie przybliżeniem dla Δ\DeltaΔy.
spójrzmy na przykład użycia tego przybliżenia:
Pytanie 4: rozważmy funkcję y = ln(x + 1)., Załóżmy, że X zmienia się z 0 do 0.01. Przybliżona Δ\DeltaΔy.
- Krok 1: zauważ, że x zmienia się z 0 Na 0.01, więc zmiana w x będzie:
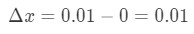
równanie 6: pytanie różnicowe pt.1 - Krok 2:
pochodna będzie:
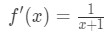
równanie 6: pytanie różnicowe pt.,2 - Krok 3:
Podłączanie wszystkiego, co mamy:
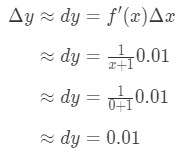
równanie 6: pytanie różnicowe pt.3 stąd Δ \ DeltaΔy ≈ \ approx≈ 0.01
jednak przez większość czasu chcemy oszacować wartość funkcji, a nie zmianę wartości. Dlatego dodamy obie strony równania przez y, co daje nam:
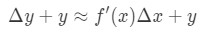
który jest taki sam jak:
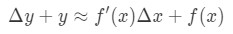
to równanie jest nieco trudne do odczytania, więc zamierzamy zmienić je jeszcze bardziej. Spróbujmy pozbyć się y i Δ\DeltaΔy. Zauważ, że Δ\DeltaΔy+ y jest w zasadzie tym samym, co znalezienie wartości funkcji przy Δ \ DeltaΔx+x. innymi słowy,
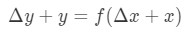
dlatego zastąpienie tego w naszym przybliżeniu powyżej da nam:
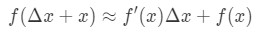
gdzie f(Δ\DeltaΔx+x) jest wartością, którą próbujemy oszacować. Jak używamy tej formuły? Polecam następujące kroki:
skorzystajmy z tych kroków w przypadku następującego pytania.
Pytanie 5: Użyj różnic do przybliżenia 10\sqrt{10}10.
- Krok 1: Porównaj f (Δ\DeltaΔx+x) z 10\sqrt{10} 10., Since 10\sqrt{10}10 has a square root and 9 is a perfect square that is closest to 10, then let
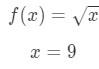
Equation 7: Approximate value with differentials pt.1 Notice that:
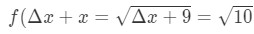
Equation 7: Approximate value with differentials pt.,2 zobacz, że nie ma wyboru, jak tylko pozwolić Δ\DeltaΔx = 1
- Krok 2:
zobacz, że pochodna daje:

równanie 7: przybliżona wartość z różnicami pt.3 oznacza to
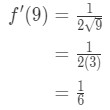
równanie 7: przybliżona wartość z różnicami pt.,4 - Krok 3:
podłączenie wszystkiego do wzoru daje nam:
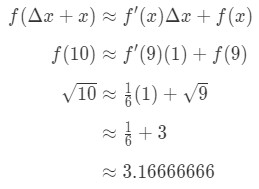
równanie 7: przybliżona wartość z różnicami pt.5 w związku z tym właśnie przybliżono liczbę.
ciekawostką jest to, że aproksymacja liniowa i różnice dają taki sam wynik dla 10\sqrt{10}10.,
Jeśli chcesz dowiedzieć się więcej o różnicach, kliknij ten link:
http://tutorial.math.lamar.edu/Classes/CalcI/LinearApproximations.aspx
dowodzenie reguły L ' Hospital za pomocą aproksymacji liniowej
teraz nauczyliśmy się wiele o aproksymacji liniowej, ale co jeszcze możemy z tym zrobić? W rzeczywistości możemy użyć wzoru aproksymacji liniowej, aby udowodnić regułę znaną jako reguła L ' Hospitala . Oto jak działa dowód.
Przypomnijmy, że wzór aproksymacji liniowej wynosi:

zobacz, że możemy zmienić wzór tak, że:
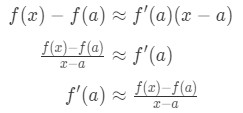
uświadom sobie, że przybliżenie staje się coraz dokładniejsze, gdy wybieramy wartości X, które są bliższe a. innymi słowy, jeśli weźmiemy granicę jako X→a, to będą one równe. Więc
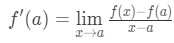
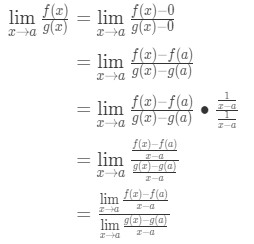
teraz zauważ, że możemy zastosować wzór, który otrzymaliśmy wcześniej tutaj. Więc teraz
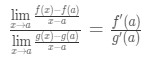
teraz zamiast pisać F'(a) i g'(A), możemy zastosować limity jako X→a (ponieważ wiemy, że F I g są różniczkowalne)., Więc
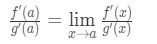
dlatego właśnie pokazaliśmy, że:
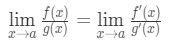
czyli reguła l ' Hospital .
kiedy używać reguły l 'chopitala
zawsze chcemy stosować regułę l' chopitala, gdy napotykamy nieokreślone granice. Istnieją dwa rodzaje form nieokreślonych., Te nieokreślone formy to:
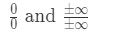
Wiele osób popełnia błąd, używając l 'chopital' s reguła bez sprawdzania, czy jest to nieokreślona granica. Więc upewnij się, że najpierw to sprawdzisz! W przeciwnym razie nie zadziała i otrzymasz złą odpowiedź. Poniżej znajduje się przewodnik po używaniu reguły l ' chopital:
- Krok 1: Oceń limit bezpośrednio.
- Krok 2: Sprawdź, czy jest to jedna z nieokreślonych form. Jeśli tak, przejdź do kroku 3.,
- Krok 3: Użyj reguły l ' chopital.
- Krok 4: Sprawdź, czy otrzymasz inny nieokreślony formularz. W takim przypadku powtórz Krok 3.
przyjrzyjmy się kilku przykładom, korzystając z tych kroków.
pytanie 6: Ocena limitu
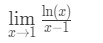
- Krok 1: Ocena limitu bezpośrednio daje nam
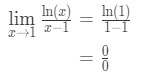
równanie 9: pytanie reguły l ' chopital pt.,2 - Krok 2:
tak, jest to jedna z nieokreślonych form.
- Krok 3:
stosując regułę l ' chopital mamy:
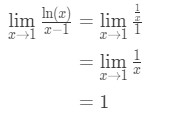
równanie 9: pytanie reguły l ' chopital pt.3 - Krok 4:
jeden nie jest nieokreśloną formą, więc skończyliśmy i odpowiedź brzmi 1.
teraz to pytanie było trochę łatwe, więc może rzućmy okiem na coś, co jest nieco trudniejsze.,
pytanie 7: Oblicz limit
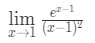
- Krok 1: Ocena limitu bezpośrednio widzimy, że:
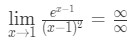
równanie 10: reguła l ' chopital dwa razy pytanie pt.2 - Krok 2:
jest to forma nieokreślona, więc przejdź do kroku 3.,
- Krok 3:
stosując regułę l ' chopital mamy
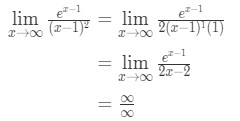
równanie 10: reguła l ' chopital dwa razy pytanie pt.3 - Krok 4:
jest to kolejna nieokreślona forma. Więc musimy wrócić do kroku 3 i zastosować ponownie Zasady l ' coptial.
- Krok 3:
ponowne zastosowanie reguły l ' chopital mamy:
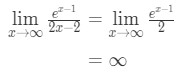
równanie 10: reguła l ' chopital dwa razy pytanie pt.,4 - Krok 4:
Nieskończoność nie jest nieokreśloną formą, więc skończyliśmy i odpowiedź brzmi ∞ \ infty∞