er is geen enkele strategie voor het vertalen van wiskundige uitdrukkingen in algebraïsche uitdrukkingen. Zolang je de basis kunt onthouden, moet je in staat zijn om de meer uitdagende degenen aan te pakken. Zorg ervoor dat je kunt rechtvaardigen hoe je met je eigen algebraïsche expressie komt, en nog belangrijker dat het zinvol is voor jou. Vraag altijd om hulp van uw leraren, als dat nodig is of werk samen met uw klasgenoten, zodat u uw antwoorden kunt verifiëren.,
om uw vaardigheden in het schrijven van algebraïsche uitdrukkingen op te bouwen, zullen we verschillende manieren bespreken hoe elke operatie als een woord of zin in het probleem kan worden weergegeven. De vier rekenkundige bewerkingen zijn optellen, aftrekken, vermenigvuldigen en delen.,
Key Words for Addition

Key Words for Subtraction

Key Words for Multiplication

Key Words for Division

It is time now time to go over some examples to practice writing algebraic expressions., Ik scheid de voorbeelden in twee:
- basisvoorbeelden van algebraïsche uitdrukkingen
- meerdelige voorbeelden van algebraïsche uitdrukkingen
Basisalgebraïsche uitdrukkingen voorbeelden
Voorbeeld 1: Schrijf een algebraïsche uitdrukking voor de wiskundige zin “de som van een getal en vier”.
oplossing: het woord ” sum ” geeft ons onmiddellijk de hint die we hier gaan toevoegen. Merk op dat we twee hoeveelheden willen toevoegen: een onbekend nummer en het nummer 4. Omdat we niet weten wat de waarde van het getal is, kunnen we een variabele gebruiken om het weer te geven., U mag alle letters van het alfabet gebruiken. Laten we in dit geval afspreken om y te gebruiken voor de variabele.
wanneer we de variabele y en 4 toevoegen, hebben we y + 4. Het is ook goed om je antwoord te schrijven als 4 + y omdat optellen commutatief is-dat wil zeggen, het wisselen van de volgorde van optellen verandert de som niet.
het uiteindelijke antwoord is y+4.
Voorbeeld 2: Schrijf een algebraïsche uitdrukking voor de wiskundige zin “10 verhoogd met een getal”.
oplossing: de trefwoorden “verhoogd met” impliceren toevoeging. Dit betekent dat een onbekend getal is toegevoegd aan 10., Met behulp van de letter k als de variabele, kunnen we het bovenstaande statement vertalen als 10 + k. aangezien optellen commutatief is, kunnen we het herschrijven als k + 10. Een van de twee hierboven is een correct antwoord.
het uiteindelijke antwoord is k+10.
Voorbeeld 3: Schrijf een algebraïsche uitdrukking voor de wiskundige zin “het verschil van 1 en een getal”.
oplossing: het woord “verschil” suggereert dat we gaan aftrekken. Bovendien, wanneer u dit wiskundige woord (verschil) tegenkomen zorg ervoor om aandacht te besteden aan de orde. Het nummer 1 komt eerst dan komt een onbekend nummer op de tweede plaats., Dat betekent dat het getal 1 het minuend is en het onbekende getal het subtrahend. Als we besluiten om de letter x als onze variabele te gebruiken, wordt het antwoord 1 − x.
het uiteindelijke antwoord is 1 – x.
Voorbeeld 4: Schrijf een algebraïsche uitdrukking voor de wiskundige zin “een getal kleiner dan 8”.
oplossing: wees zeer voorzichtig bij het omgaan met de sleutelwoorden “minder dan”. De eerste hoeveelheid die voor de “minder dan” sleutelwoorden komt die “een getal” is, is het subtrahend. Terwijl de hoeveelheid die daarna komt het minuend wordt.,
met andere woorden, we gaan het onbekende getal aftrekken van het getal 8. Als we onze variabele als letter A kiezen, krijgen we 8 − a.
het uiteindelijke antwoord is 8-a.
Voorbeeld 5: Schrijf een algebraïsche uitdrukking voor de wiskundige zin “het product van 5 en een getal”.
oplossing: om het product van twee hoeveelheden of waarden te vinden, betekent dit dat we ze samen zullen vermenigvuldigen. Als u de letter m selecteert als onze variabele, is de algebraïsche uitdrukking voor deze wiskundezin gewoon 5m. het betekent 5 keer het onbekende getal m.
het uiteindelijke antwoord is 5m.,
Voorbeeld 6: Schrijf een algebraïsche uitdrukking voor de wiskundige zin “twee keer een getal”.
oplossing: het woord “twee keer” betekent dat we iets gaan verdubbelen. In dit geval willen we een onbekende waarde of hoeveelheid verdubbelen. Laat de letter d het onbekende getal zijn, als we het verdubbelen krijgen we de algebraïsche uitdrukking 2d.
het uiteindelijke antwoord is 2d.
Voorbeeld 7: Schrijf een algebraïsche uitdrukking voor de wiskundige zin “het quotiënt van een getal en 7”.
oplossing: het trefwoord “quotiënt” betekent dat we de operatie van deling uitvoeren. We delen een onbekend getal door 7., Door de letter w als onze variabele te kiezen, kan de wiskundige zin hierboven worden uitgedrukt als de algebraïsche uitdrukking hieronder.
\LARGE{w \ over 7}
Voorbeeld 8: Schrijf een algebraïsche uitdrukking voor de wiskundige zin “de verhouding van 10 en een getal”.
oplossing: evenzo betekent het woord “verhouding” delen. De volgorde hier is erg belangrijk. De eerste hoeveelheid is het getal 10 en de tweede hoeveelheid is het onbekende getal. Dat betekent dat 10 gedeeld wordt door een onbekend getal., Laat c het onbekende getal zijn, de algebraïsche uitdrukking voor de wiskundige zin hierboven kan worden geschreven als
\LARGE{10 \ over c}
meerdelige algebraïsche uitdrukkingen voorbeelden
Deze keer zullen we wiskundige uitdrukkingen behandelen die iets complexer zijn. De algebraïsche uitdrukkingen kunnen hier twee of meer bewerkingen bevatten. De basis zoekwoorden die we eerder leren zullen dienen als de basis als we werken aan de meer uitdagende wiskundige zinnen te interpreteren in algebraïsche uitdrukkingen.,
Voorbeeld 1: Schrijf een algebraïsche uitdrukking voor de wiskundige zin”3 meer dan tweemaal een getal”.
oplossing: om dit veel gemakkelijker te begrijpen, gaan we deze zin in twee delen verdelen. Ten eerste, erken dat we een onbekend nummer hebben. We kunnen het weergeven met alle letters van het alfabet. Laat het onbekende getal de variabele x zijn. het diagram hieronder zou ons moeten helpen om te zien wat er echt aan de hand is.,
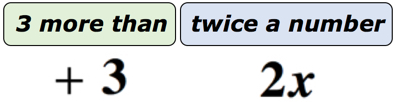
als je erover nadenkt, is er een onbekend getal vertegenwoordigd door variabele x dat wordt verdubbeld of vermenigvuldigd met 2. Wat het product ook is, we zullen er 3 aan toevoegen. Dus, ons definitieve antwoord moet eruit zien als het ene hieronder.
het uiteindelijke antwoord is 2x + 3.
Voorbeeld 2: Schrijf een algebraïsche uitdrukking voor de wiskundige zin “het verschil van een half getal en 10”.
oplossing: stel dat de variabele y het onbekende getal is., Het trefwoord “verschil” vraagt ons dat we gaan aftrekken. Het is hier van cruciaal belang dat we aandacht besteden aan de volgorde van Aftrekken. Na het woord “verschil”, moeten we twee hoeveelheden verwachten. De eerste zal het minuend zijn, terwijl de tweede het subtrahend zal zijn. Neem een kijkje op het diagram hieronder.
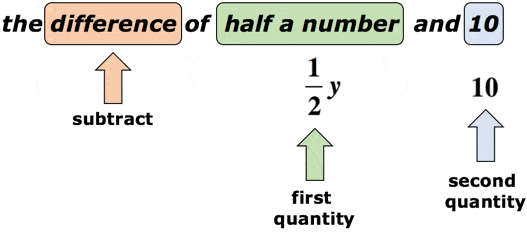
verwijzend naar het bovenstaande diagram trekken we de eerste hoeveelheid af met de tweede hoeveelheid. Met andere woorden, de tweede hoeveelheid wordt afgetrokken van de eerste hoeveelheid., Het uiteindelijke antwoord voor wiskundige zin zou iets als dit moeten hebben,
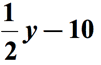
Voorbeeld 3: Schrijf een algebraïsche uitdrukking voor de wiskundige zin”7 minder dan het product van een getal en 6″.
oplossing: we weten dat “minder dan” suggereert een aftrekking operatie. Maar we moeten hier een beetje voorzichtig zijn, want de volgorde van hoe we Aftrekken is belangrijk. Stel dat het onbekende getal wordt weergegeven door de variabele k. laten we dit op een diagram zetten om er een zin van te maken.,
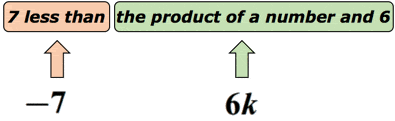
in feite kan deze wiskundige zin worden herschreven als
” het product van een getal en 6 min 7 “
De “7 minder dan” betekent “min 7” tot welke hoeveelheid dan ook beschreven die in dit geval “het product van een nummer en 6”. Hier is de uiteindelijke interpretatie van de wiskundige zin in een algebraïsche uitdrukking:
6k-7
Voorbeeld 4: Schrijf een algebraïsche uitdrukking voor de wiskundige zin “Het gemiddelde van een getal en 4”.,
oplossing: om aan de slag te gaan met deze specifieke wiskundige zin, moeten we bekijken wat het woord “gemiddeld” betekent. Om het gemiddelde of gemiddelde van twee of meer getallen te berekenen, moeten we alle getallen optellen om een som te krijgen en deze vervolgens delen door het aantal items of hoeveel getallen er zijn. Als we m de variabele laten zijn om het onbekende getal voor te stellen, kan de wiskundige zin hierboven worden uitgedrukt in algebraïsche uitdrukkingen als,
\LARGE{{m + 4} \over 2}
Voorbeeld 5: Schrijf een algebraïsche uitdrukking voor de wiskundige zin “het quotiënt van 1, en 1 verminderd met een getal”.,
oplossing: het trefwoord “quotiënt” betekent dat we zullen delen. In dit geval willen we het getal 1 delen door de hoeveelheid 1 verminderd door een getal. Hieronder is de algebraïsche uitdrukking die de wiskundige zin hierboven kan vertegenwoordigen. Laat a het onbekende nummer zijn.
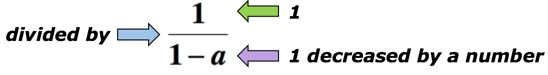
Voorbeeld 6: Schrijf een algebraïsche uitdrukking voor de wiskundige zin “een derde van het kwadraat van een getal, verhoogd met 2”.
oplossing: er zijn hier een paar dingen aan de hand., Ten eerste kan het deel van de zinsnede dat zegt “een derde van het kwadraat van een getal” worden geïnterpreteerd als ” het kwadraat van een getal gedeeld door 3 “. We moeten het onbekende getal verhogen met 2 en dan delen door 3. Stel dat het onbekende getal t is, dan krijgen we
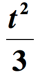
We zijn nog niet klaar. De laatste stap die moet worden gedaan, is de bovenstaande hoeveelheid met 2 toe te voegen om het resterende deel van de zinsnede ” verhoogd met 2 “op te nemen. Hier is de laatste weergave van de gegeven wiskundezin.,
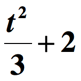
You might also be interested in:
Algebraic Expressions
Algebraic Sentences Word Problems