Non esiste un’unica strategia per tradurre frasi matematiche in espressioni algebriche. Finché si può ricordare le basi, si dovrebbe essere in grado di affrontare quelli più impegnativi. Basta fare in modo che si può giustificare come si arriva con la propria espressione algebrica, e ancora più importante che ha senso per voi. Chiedi sempre aiuto ai tuoi insegnanti, se necessario o collabora con i tuoi compagni di classe in modo da poter verificare le tue risposte.,
Per costruire le vostre abilità nella scrittura di espressioni algebriche, andremo oltre diversi modi di come ogni operazione può presentarsi come una parola o una frase nel problema. Le quattro operazioni aritmetiche coinvolte sono addizione, sottrazione, moltiplicazione e divisione.,
Key Words for Addition

Key Words for Subtraction

Key Words for Multiplication

Key Words for Division

It is time now time to go over some examples to practice writing algebraic expressions., Ho separato gli esempi in due:
- esempi di Base di espressioni algebriche
- Multi-parte esempi di espressioni algebriche
di Base di Espressioni Algebriche Esempi
Esempio 1: Scrivere un’espressione algebrica per la matematica frase ” la somma di un numero e quattro”.
Soluzione: La parola “somma” ci dà immediatamente il suggerimento che stiamo per aggiungere qui. Si noti che vogliamo aggiungere due quantità: un numero sconosciuto e il numero 4. Poiché non sappiamo quale sia il valore del numero, possiamo usare una variabile per rappresentarlo., È possibile utilizzare tutte le lettere dell’alfabeto. In questo caso, accettiamo di usare y per la variabile.
Quando aggiungiamo la variabile y e 4, abbiamo y + 4. Va anche bene scrivere la tua risposta come 4 + y perché l’aggiunta è commutativa-cioè, cambiare l’ordine di aggiunta non cambia la sua somma.
La risposta finale è y+4.
Esempio 2: Scrivi un’espressione algebrica per la frase matematica “10 aumentato di un numero”.
Soluzione: Le parole chiave “aumentato di” implicano un’aggiunta. Ciò significa che un numero sconosciuto è stato aggiunto a 10., Usando la lettera k come variabile, possiamo tradurre l’istruzione sopra come 10 + k. Poiché l’aggiunta è commutativa, possiamo riscriverla come k + 10. Uno dei due sopra è una risposta corretta.
La risposta finale è k+10.
Esempio 3: Scrivi un’espressione algebrica per la frase matematica “la differenza di 1 e un numero”.
Soluzione: La parola “differenza” suggerisce che stiamo per sottrarre. Inoltre, quando incontri questa parola matematica (differenza) assicurati di prestare attenzione all’ordine. Il numero 1 viene prima poi un numero sconosciuto arriva secondo., Ciò significa che il numero 1 è il minuend e il numero sconosciuto è il subtrahend. Se decidiamo di utilizzare la lettera x come variabile, la risposta diventa 1-x.
La risposta finale è 1 – x.
Esempio 4: Scrivi un’espressione algebrica per la frase matematica”un numero inferiore a 8″.
Soluzione: fai molta attenzione quando hai a che fare con le parole chiave “less than”. La prima quantità che precede le parole chiave” meno di “che è” un numero ” è il subtrahend. Mentre la quantità che viene dopo diventa il minuend.,
In altre parole, stiamo per sottrarre il numero sconosciuto dal numero 8. Se scegliamo la nostra variabile come lettera a, otteniamo 8-a.
La risposta finale è 8 – a.
Esempio 5: Scrivi un’espressione algebrica per la frase matematica”il prodotto di 5 e un numero”.
Soluzione: per trovare il prodotto di due quantità o valori, significa che li moltiplicheremo insieme. Selezionando la lettera m come variabile, l’espressione algebrica per questa frase matematica è semplicemente 5m. Significa 5 volte il numero sconosciuto m.
La risposta finale è 5m.,
Esempio 6: Scrivi un’espressione algebrica per la frase matematica “due volte un numero”.
Soluzione: La parola “due volte” significa che stiamo per raddoppiare qualcosa. In questo caso, vogliamo raddoppiare un valore o una quantità sconosciuta. Lascia che la lettera d sia il numero sconosciuto, quando la raddoppiamo otteniamo l’espressione algebrica 2d.
La risposta finale è 2d.
Esempio 7: Scrivi un’espressione algebrica per la frase matematica “il quoziente di un numero e 7”.
Soluzione: La parola chiave “quoziente” significa che stiamo eseguendo l’operazione di divisione. Divideremo un numero sconosciuto per 7., Scegliendo la lettera w come variabile, la frase matematica sopra può essere espressa come espressione algebrica sotto.
\LARGE{w \over 7}
Esempio 8: Scrivi un’espressione algebrica per la frase matematica ” il rapporto tra 10 e un numero”.
Soluzione: allo stesso modo, la parola “rapporto” significa divisione. L’ordine qui è molto importante. La prima quantità è il numero 10 e la seconda quantità è il numero sconosciuto. Ciò significa che 10 è diviso per un numero sconosciuto., Sia c il numero sconosciuto, l’espressione algebrica per la frase matematica sopra può essere scritta come
\LARGE{10 \over c}
Espressioni algebriche in più parti Esempi
Questa volta, ci occuperemo di frasi matematiche che sono un po ‘ più complesse. Le espressioni algebriche qui possono contenere due o più operazioni. Le parole chiave di base che impariamo prima serviranno come base mentre lavoriamo con le frasi matematiche più impegnative da interpretare in espressioni algebriche.,
Esempio 1: Scrivi un’espressione algebrica per la frase matematica “3 più del doppio di un numero”.
Soluzione: Per rendere questo molto più facile da capire, divideremo questa frase in due parti. In primo luogo, riconoscere che abbiamo un numero sconosciuto. Possiamo rappresentarlo con qualsiasi lettera dell’alfabeto. Lascia che il numero sconosciuto sia la variabile x. Lo schema seguente dovrebbe aiutarci a vedere cosa sta realmente succedendo.,
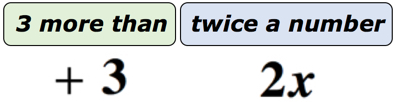
Se ci pensate, c’è un numero sconosciuto rappresentato dalla variabile x che viene raddoppiato o moltiplicato per 2. Qualunque sia il prodotto, aggiungeremo 3 ad esso. Quindi, la nostra risposta finale dovrebbe essere simile a quella qui sotto.
La risposta finale è 2x + 3.
Esempio 2: Scrivi un’espressione algebrica per la frase matematica “la differenza di mezzo numero e 10”.
Soluzione: Supponiamo che la variabile y sia il numero sconosciuto., La parola chiave “differenza” ci suggerisce che stiamo per eseguire la sottrazione. È fondamentale qui prestare attenzione all’ordine di sottrazione. Dopo la parola “differenza”, dovremmo aspettarci due quantità. Il primo sarà il minuend, mentre il secondo sarà il subtrahend. Date un’occhiata al diagramma qui sotto.
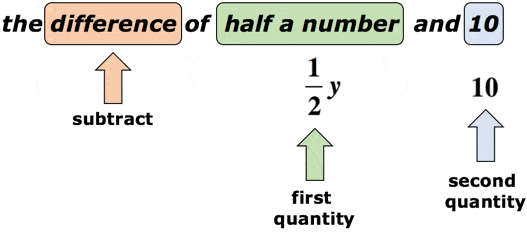
Facendo riferimento al diagramma sopra, sottrarremo la prima quantità per la seconda quantità. In altre parole, la seconda quantità viene sottratta dalla prima quantità., La risposta finale per la frase matematica dovrebbe essere simile a questa,
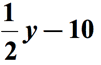
Esempio 3: Scrivi un’espressione algebrica per la frase matematica “7 meno del prodotto di un numero e 6”.
Soluzione: Sappiamo che “less than” suggerisce un’operazione di sottrazione. Ma dobbiamo stare un po ‘ attenti qui perché l’ordine su come sottraiamo è importante. Supponiamo che il numero sconosciuto sia rappresentato dalla variabile k. Mettiamo questo su un diagramma per dare un senso a questo.,
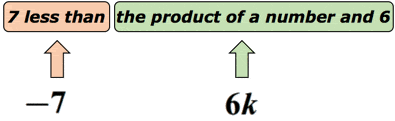
in Realtà, questa espressione matematica può essere riscritto come:
” il prodotto di un numero e il 6 meno 7 “
“7 meno” significa “meno 7” per qualsiasi quantità essere descritto, in questo caso, “il prodotto di un numero e 6”. Ecco l’interpretazione finale della frase matematica in un’espressione algebrica:
6k-7
Esempio 4: Scrivi un’espressione algebrica per la frase matematica”la media di un numero e 4″.,
Soluzione: Per iniziare su questa particolare frase matematica, dobbiamo rivedere cosa significa la parola “media”. Per calcolare la media o la media di due o più numeri, dovremo sommare tutti i numeri per ottenere una somma, quindi dividerla per il numero di voci o quanti numeri ci sono. Se lasciamo che m sia la variabile per rappresentare il numero sconosciuto, la frase matematica sopra può essere espressa in espressioni algebriche come,
\LARGE{{m + 4} \over 2}
Esempio 5: Scrivi un’espressione algebrica per la frase matematica ” il quoziente di 1 e 1 diminuito di un numero”.,
Soluzione: La parola chiave “quoziente” significa che divideremo. In questo caso, vogliamo dividere il numero 1 per la quantità 1 diminuita di un numero. Di seguito è riportata l’espressione algebrica che può rappresentare la frase matematica sopra. Lasciate che un essere il numero sconosciuto.
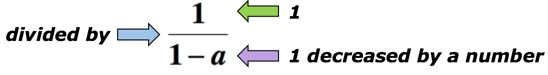
Esempio 6: Scrivere un’espressione algebrica per la matematica frase “un terzo del quadrato di un numero, aumentato di 2”.
Soluzione: ci sono alcune cose in corso qui., In primo luogo, la parte della frase che afferma ” un terzo del quadrato di un numero ” può essere interpretata come ” il quadrato di un numero diviso per 3 “. Avremo bisogno di aumentare il numero sconosciuto di 2 quindi dividere per 3. Supponiamo che il numero sconosciuto sia t, otteniamo
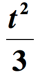
Non abbiamo ancora finito. L’ultimo passo da fare è aggiungere la quantità sopra di 2 per incorporare la parte rimanente della frase ” aumentata di 2 “. Quindi ecco la rappresentazione finale della frase matematica data.,
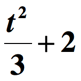
You might also be interested in:
Algebraic Expressions
Algebraic Sentences Word Problems