lineáris közelítés
tegyük fel, hogy egy nap elfelejtette a számológép, és tényleg szeretné megtalálni, hogy mi a négyzetgyöke 2 jelentése. Hogyan tudnánk meg számológép nélkül? Tudjuk használni lineáris közelítés!
egy függvény Linearizálása
egy függvény linearizálása csak arról szól, hogy a függvény érintővonalát egy adott ponton másképp találjuk meg., A linearizációs képlet a következő:

ahol L(x) a tangens vonal egyenlete az a pontban.
hogyan hasznos ez számunkra? Nos, valójában ezt az egyenletet felhasználhatjuk a függvény közelítő értékeire az a pont közelében. vessen egy pillantást erre a grafikonra.,
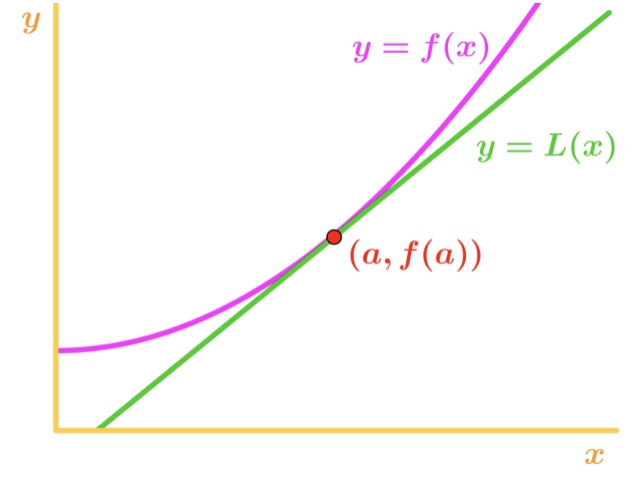
figyeljük meg, hogy az x értékek esetében az a pont közelében azt látjuk, hogy a függvény és a tangens vonal viszonylag közel egymáshoz. Emiatt meg tudjuk írni, hogy a funkció megközelítőleg megegyezik az a pont közelében lévő érintővonallal., Más szóval,

ahol \≈a kb. Ezt az egyenletet lineáris közelítési képletnek nevezik. Lineáris abban az értelemben, hogy az érintő egyenes vonal, és a függvény közelítésére használjuk. Ezzel a közelítéssel képesek vagyunk közelíteni azokat az értékeket, amelyeket kézzel nem lehet megtenni. Például a 2 négyzetgyöke vagy az 5 természetes naplója mind közelíthető!, Egy fontos dolog megjegyezni, hogy ez a közelítés csak akkor működik, x értékek közelében pont a. Ha van egy x érték messze pont a, akkor a közelítés válik igazán pontatlan.
most ne vessünk egy pillantást néhány példára egy függvény linearizációjának megtalálására, majd nézzük meg, hogyan kell használni a lineáris közelítést!
keresse meg a linearizálással az L(x) függvény a
1. Kérdés: úgy a funkció
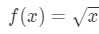
mondjuk, hogy a függvény linearizációját az a=4 pontban akarjuk megtalálni.
az L(x) linearizáció megtalálásához emlékezzünk arra, hogy

- 1.lépés: Keressen egy
- 2. lépés: Keresse meg az f(A)
- 3. lépés: Keresse meg az f ” (a).
- 4. lépés: Csatlakoztassa mindhárom képletet az L(x)
-
let ‘ s follow these steps!,
1. lépés: szerencsére a = 4-et adunk nekünk a kérdésben,így nem kell keresnünk.
- 2. lépés:
vegye figyelembe, hogy
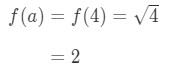
1.egyenlet: Linearizációs kérdés pt. 3 - 3. lépés:
tudja, hogy a négyzetgyökek származéka
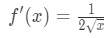
1. egyenlet: Linearizációs kérdés pt., 4 And so plugging in x=a gives us:
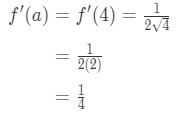
Equation 1: Linearization question pt. 5 - Step 4:
Since we know a, f(a), and f'(a), we can now plug it into L(x) to find the linearization of f(x).
Hence,
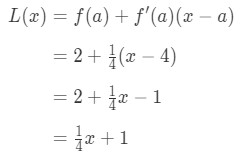
Equation 1: Linearization question pt., 6 So L(x)=14\frac{1}{4}41x+1 ennek a függvénynek a linearizálása az x=4 pontban. Ezenkívül ez a függvény érintővonala is az x=4 pontban.
hogyan kell csinálni lineáris közelítés
ne feledje, korábban azt mondtuk, hogy az érintővonal egyenletét használhatjuk a függvény közelítő értékeihez az a közelében? Próbáljuk ki ezt a korábban talált linearizációval. Emlékezzünk vissza, hogy
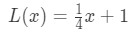
az x=4-hez közeli pontoknál. Ezt az f(x) lineáris közelítésévé változtathatjuk úgy, hogy:
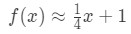
most tegyük fel, hogy hozzávetőleges f(4.04). Ha ezt csatlakoztatná az eredeti funkcióhoz, akkor 4.04\sqrt{4.04}4.04-et kapna . Ezt nagyon nehéz lenne kalkulátor nélkül kiszámítani., Lineáris közelítéssel azonban azt mondhatjuk, hogy

eddig ezek a kérdések adtak nekünk egy függvényt és egy pontot, amivel dolgozhatunk. Mi van, ha ezek közül egyiket sem adták meg? Mi van, ha a kérdés csak azt mondja nekünk, hogy becsüljük meg a számot?
használjon lineáris közelítést a
szám becsléséhez tegyük fel, hogy 10\sqrt{10}10-et szeretnénk becsülni. Hogy csináljuk?, A lineáris közelítést kell használnunk

de még egy függvényünk és egy pontunk sincs, amivel dolgozhatnánk. Ez azt jelenti, hogy magunknak kell elkészítenünk őket. Ez vezet bennünket, hogy a következő lépéseket:
- 1. Lépés: hozzon létre egy funkciót
- 2. Lépés: hozzon létre a pont
- 3. Lépés: keresse meg az f(a) f'(a)
- 4. Lépés: Csatlakoztassa mindent a lineáris közelítés formula
kövessük a lépéseket!,
2. kérdés: becsülje meg a 10\sqrt{10}10
- 1. lépés: jöjjön létre egy funkció. Vegye figyelembe, hogy a
3. egyenlet: becslés lineáris kb. pt.2 valahogy kapcsolatot kell teremteni f(x) és 10\sqrt{10}10 között. Nem mondhatjuk, hogy f(x) = 10\sqrt{10}10, mert a függvény nem függ x-től. Let
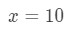
3.egyenlet: becslés lineáris kb. pt.,3 ha ezt tesszük, akkor alapvetően azt mondjuk, hogy
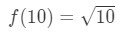
3 egyenlet: becsülje meg lineáris kb. pt.4 most nyilvánvalóan elmondhatjuk, hogy mi legyen a funkció. Let
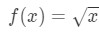
3.egyenlet: becslés lineáris kb. pt.5 tehát van egy funkciónk, de most szükségünk van egy a pontra, amellyel dolgozhatunk.,
- 2. lépés:
a megfelelő a érték megtalálásának kulcsa két dolog megfontolása:
1) Győződjön meg róla, hogy az a érték közel van x
2) Győződjön meg róla, hogy az f(a) szép szám.
elegendő lenne az a = 8? Jól, 8 elég közel 10 így nem rossz. Azonban
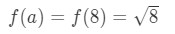
3. egyenlet: becslés lineáris kb. pt.6 vegye figyelembe, hogy a 8\sqrt{8}8 nem túl szép szám. Valójában egy csomó tizedes számot kap. Tehát ki kell próbálnunk valami mást.,
elegendő lenne az a = 9? Újra, 9 elég közel 10 így rendben van. Is,

egyenlet 3: becslés lineáris kb. pt.7 f(A) valójában egy szép egész szám itt, így ez valóban működik! Tehát az a=9 kiválasztása elegendő.
- 3. lépés:
vegye figyelembe, hogy a korábbi:

3. egyenlet: becslés lineáris kb. pt.,8 Calculating f'(x) we have again:

Equation 3: Estimate with linear approx. pt.9 So
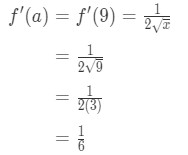
Equation 3: Estimate with linear approx. pt.,10 - Step 4:
Going back to the linear approximation formula we have:

Equation 3: Estimate with linear approx. pt.11 Plugging a, f(a), f'(a), f(x), and x in our formula you will see that:

Equation 3: Estimate with linear approx. pt.12 Hence, we just approximated the number!,
Ha további gyakorlati problémákat szeretne a lineáris közelítéssel kapcsolatban, akkor azt javaslom, hogy nézze meg ezt a linket itt.
http://tutorial.math.lamar.edu/Classes/CalcI/LinearApproximations.aspx
túlbecsülni és alábecsülni
tudjuk, hogy a lineáris közelítés csak egy becslés a függvény értékét egy meghatározott ponton. Honnan tudjuk azonban, hogy ha becslésünk túlbecsült vagy alábecsült? Kiszámoljuk a második származékot, és megnézzük a konkávságot.,
konkáv fel vs konkáv le
Ha a függvény második származéka nagyobb, mint 0 az a közelében lévő értékek esetében,akkor a függvény homorú. Ez azt jelenti, hogy a közelítés lesz alábecsülik. Más szóval,
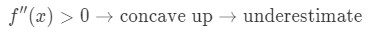
miért? Vessünk egy pillantást erre a grafikonra.,
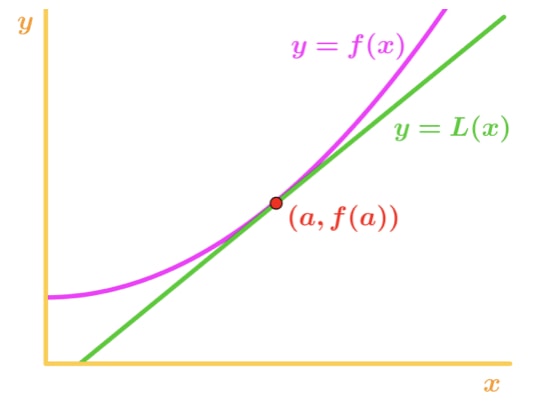
Megjegyzés: f(x) felfelé konkáv, a tangens vonal pedig f(x) alatt található. Tegyük fel, hogy az érintővonalat az f(x) megközelítésére használjuk. Ezután az érintővonal y értékei mindig kisebbek lesznek, mint az F(x) tényleges értéke. Ezért van egy alábecsült
most, ha a függvény második származéka kevesebb, mint 0 az a közelében lévő értékek esetében,akkor a függvény homorú., Ez azt jelenti, hogy közelítésünk túlbecsülni fog. Más szóval,
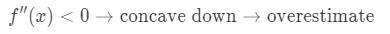
ismét, miért? Vessünk egy pillantást egy másik grafikonra.
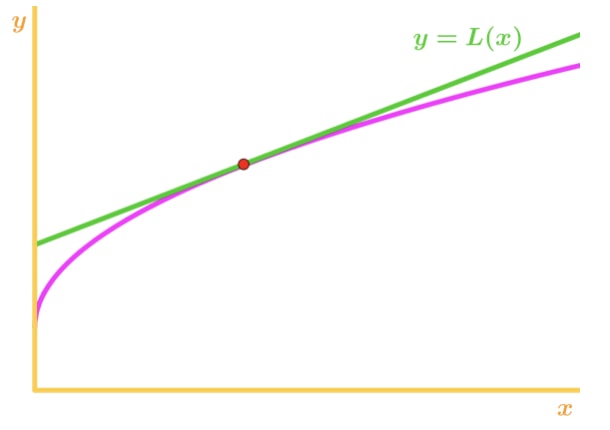
vegye figyelembe, hogy f(x) konkáv, és a tangens vonal közvetlenül F(x). Ismét azt mondjuk, hogy az érintővonalat az f(x) megközelítésére fogjuk használni., Ezután az érintővonal y értékei mindig nagyobbak lesznek, mint az F(x) tényleges értéke. Ezért túlbecsüljük.
Tehát, ha valaha is kell látni, hogy az érték egy alábecsült, vagy egy túlzó, győződjön meg róla, hogy kövesse az alábbi lépéseket:
- 1. Lépés: keresse meg a második származtatott
- 2. Lépés: nézd meg a homorúság a funkció mellett a pont
- 3. Lépés: Ellenőrizze, hogy ez egy becsüld le/túlbecsülni
nézzük a példát:
3. Kérdés: f(x) = x\sqrt{x}x a = 4. Ha lineáris hozzávetőleges f (4.,04), túlbecsülni vagy alábecsülni?
- 1. lépés: lásd, hogy
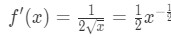
4.egyenlet: túlbecsülni kérdés pt.1 tehát a második származék
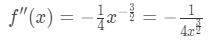
egyenlet 4: túlbecsülni kérdés pt.2 - 2.lépés:
vegye figyelembe, hogy a=4, Ezért az x pozitív értékeit 4 közelében szeretnénk megnézni. Most nézd meg a második származékot., Ha x pozitív, azt látjuk, hogy
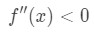
egyenlet 4: túlbecsülni kérdés pt.3 ezért konkáv le
- 3.lépés:
tudjuk, hogy ha a függvény konkáv le, akkor az érintő vonal lesz a függvény felett. Ezért az érintővonal közelítésként történő használata túlbecsült értéket ad.
differenciák
nem csak a lineáris közelítéssel közelíthetjük meg az értékeket,hanem a differenciákkal is közelíthetjük., Közelíteni, akkor használja a következő képlet
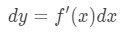
amennyiben dy s dx vannak különbségek, az f'(x) a származékos f tekintve az x-et. Mivel van dolgunk, nagyon kis változások x, illetve y, akkor fogjuk használni azt a tényt, hogy:
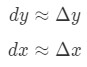
azonban a legtöbb kérdésünk a
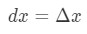
tehát ezeknek a tényeknek a használata a következőkhöz vezet:
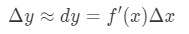
Ez a közelítés nagyon hasznos, ha közelíti a változás y., Ne feledje, akkoriban nem voltak számológépek, tehát ez a legjobb közelítés, amelyet négyzetgyökérrel vagy természetes rönkökkel rendelkező funkciókhoz kaphatnak.
a legtöbb időt meg kell keresni f ‘ (x) és Δ \ DeltaΔx magát. Más szavakkal, kövesse ezeket a lépéseket a Δ\DeltaΔy közelítéséhez!
- 1. lépés: Keresse meg a Δ \ DeltaΔx
- 2. lépés: Keresse meg az f ‘ (x)
- 3. lépés: Csatlakoztassa mindent a képletbe a Dy megtalálásához. Dy lesz a közelítés Δ \ DeltaΔy.
nézzünk egy példát ennek a közelítésnek a használatára:
4. kérdés: Tekintsük az y = ln(x + 1) funkciót., Tegyük fel, hogy az x 0-ról 0,01-re változik. Hozzávetőleges Δ \ DeltaΔy.
- 1. lépés: Vegye figyelembe, hogy x 0-ról 0,01-re változik, így az X változása a következő lenne:
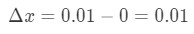
6.egyenlet: differenciális kérdés pt.1 - 2.lépés:
a származék a következő lenne:
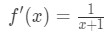
6. egyenlet: differenciális kérdés pt.,2 - 3.lépés:
mindent Bedugunk, ami van:
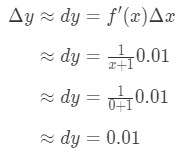
6. egyenlet: differenciális kérdés pt.3 ezért Δ\DeltaΔy ≈\kb.≈ 0.01
a függvény értékét a legtöbb esetben meg akarjuk becsülni, nem pedig az érték változását. Ezért az egyenlet mindkét oldalát y-vel adjuk hozzá, amely megadja nekünk:
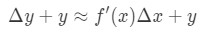
ami ugyanaz, mint:
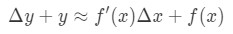
Ez az egyenlet egy kicsit nehéz olvasni, ezért még inkább átrendezzük. Próbáljunk megszabadulni y-tól és Δ\DeltaΔy-tól. Figyeljük meg, hogy Δ \ DeltaΔy + y alapvetően ugyanaz, mint megtalálni az értékét a függvény Δ \ DeltaΔx + x. más szóval,
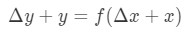
így helyettesítve ezt a fenti közelítésben:
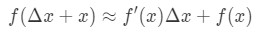
ahol f(Δ\DeltaΔx+x) az érték, amelyet megpróbálunk megbecsülni. Hogyan használjuk ezt a képletet? A következő lépéseket javaslom:
használjuk ezeket a lépéseket a következő kérdésre.
5. kérdés: használjon differenciálokat a hozzávetőleges 10\sqrt{10}10-hez.
- 1. lépés: hasonlítsa össze az f(Δ\DeltaΔx+x) értéket a 10\sqrt{10}10 értékkel., Since 10\sqrt{10}10 has a square root and 9 is a perfect square that is closest to 10, then let
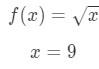
Equation 7: Approximate value with differentials pt.1 Notice that:
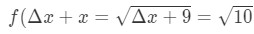
Equation 7: Approximate value with differentials pt.,2 lásd, hogy nincs más választása, mint hogy hagyja Δ\DeltaΔx = 1
- 2.lépés:
lásd, hogy a származék ad:

7. egyenlet: hozzávetőleges érték a PT különbségekkel.3 tehát ez azt jelenti, hogy
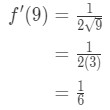
7 egyenlet: hozzávetőleges érték differenciálértékekkel pt.,4 - 3.lépés:
mindent Bedugunk a képletbe:
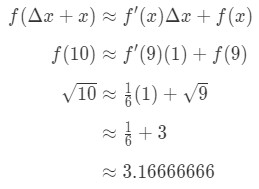
7 egyenlet: hozzávetőleges érték a PT differenciálatokkal.5 ezért csak közelítettük a számot.
egy érdekes dolog megjegyezni, hogy a lineáris közelítés és a differenciálszámok egyaránt ugyanazt az eredményt adják 10\sqrt{10}10.,
Ha többet szeretne megtudni a különbségekről, kattintson erre a linkre:
http://tutorial.math.lamar.edu/Classes/CalcI/LinearApproximations.aspx
bizonyítva L ‘ Hospital szabályát lineáris közelítéssel
most sokat tanultunk a lineáris közelítésről, de mi mást tehetünk vele? A lineáris közelítési képlet segítségével bizonyíthatjuk a L ‘ Hospital szabályának nevezett szabályt . Így működik a bizonyíték.
emlékezzünk arra, hogy a lineáris közelítési képlet:

lásd, hogy átrendezhetjük a képletet úgy, hogy:
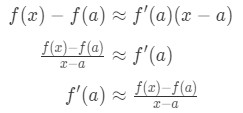
rájönnek, hogy a közelítés egyre pontosabbá válik, amikor x értékeket választunk, amelyek közelebb állnak a. más szóval, ha a határértéket x→a-ként vesszük, akkor egyenlőek lesznek. Tehát
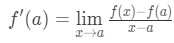
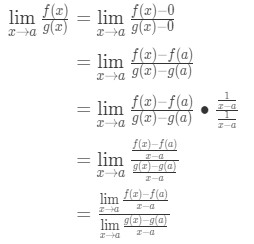
most vegye figyelembe, hogy itt alkalmazhatjuk a korábban származtatott képletet. Tehát most
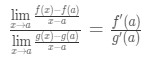
most az f “(A) és g ” (A) írás helyett X→a (mert tudjuk, hogy az f és a g differenciálható) korlátokat alkalmazhatunk., Tehát
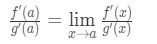
ezért csak megmutattuk, hogy:
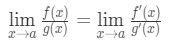
ami a L ‘ Hospital szabálya .
mikor kell használni a L ‘ Hopital szabályát
mindig azt szeretnénk alkalmazni, ha határozatlan korlátokkal találkozunk. Kétféle határozatlan forma létezik., Ezek a meghatározatlan formák a következők:
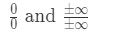
sok ember hibázik a l ‘Hopital’ s szabály anélkül, hogy ellenőrizné, hogy ez határozatlan határ. Tehát győződjön meg róla, hogy először ellenőrizze! Ellenkező esetben nem fog működni, és rossz választ kap. Itt található egy útmutató a L ‘ Hopital szabályának használatához:
- 1.lépés: értékelje közvetlenül a határértéket.
- 2. lépés: Ellenőrizze, hogy ez az egyik meghatározatlan forma. Ha igen, lépjen a 3. lépésre.,
- 3. lépés: használja a L ‘ Hopital szabályát.
- 4. lépés: Ellenőrizze, hogy kap-e egy másik meghatározatlan formát. Ismételje meg a 3. lépést, ha igen.
vessünk egy pillantást néhány példára ezekkel a lépésekkel.
6. kérdés: értékelje a határértéket
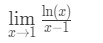
- 1. lépés: a határérték közvetlen értékelése
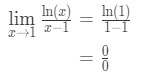
9. egyenlet: L ‘ Hopital szabálykérdése pt.,2 - 2.lépés:
Igen, ez az egyik meghatározatlan forma.
- 3. lépés:
A L ‘Hopital szabályának alkalmazása:
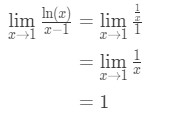
9.egyenlet: L ‘ Hopital szabálykérdése pt.3 - 4.lépés:
az egyik nem meghatározatlan forma, tehát végeztünk, a válasz pedig 1.
most ez a kérdés egy kicsit könnyű volt, akkor miért nem nézünk meg valamit, ami egy kicsit nehezebb.,
7. kérdés: értékelje a határértéket
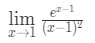
- 1. lépés: a határérték közvetlen értékelése azt látjuk, hogy:
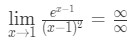
egyenlet 10: L ‘ hovital szabálya kétszer kérdés pt.2 - 2.lépés:
Ez egy meghatározatlan forma, tehát menjen a 3. lépéshez.,
- 3. lépés:
A L ‘ Hopital szabályának alkalmazása
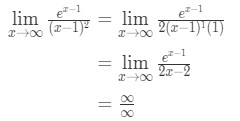
10. egyenlet: L ‘ Hopital szabálya kétszeri kérdés pt.3 - 4.lépés:
Ez egy másik meghatározatlan forma. Tehát vissza kell térnünk a 3. lépéshez, és újra alkalmaznunk kell a L ‘ optial szabályait.
- 3. lépés:
A L ‘Hopital szabályának ismételt alkalmazása:
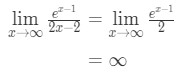
10. egyenlet: L ‘ Hopital szabálya kétszeri kérdés pt.,4 - 4. lépés:
Az Infinity nem meghatározatlan forma, tehát kész vagyunk, és a válasz ∞ \ infty∞