Il n’y a pas de stratégie unique pour traduire des phrases mathématiques en expressions algébriques. Tant que vous vous souvenez des bases, vous devriez être capable de vous attaquer aux plus difficiles. Assurez-vous simplement que vous pouvez justifier la façon dont vous venez avec votre propre expression algébrique, et plus important encore que cela a du sens pour vous. Demandez toujours de l’aide à vos enseignants, au besoin ou collaborez avec vos camarades de classe afin que vous puissiez vérifier vos réponses.,
pour développer vos compétences dans l’écriture d’expressions algébriques, nous allons passer en revue différentes façons de voir comment chaque opération peut apparaître comme un mot ou une phrase dans le problème. Les quatre opérations arithmétiques impliquées sont l’addition, la soustraction, la multiplication et la division.,
Key Words for Addition

Key Words for Subtraction

Key Words for Multiplication

Key Words for Division

It is time now time to go over some examples to practice writing algebraic expressions., Je sépare les exemples en deux:
- exemples de base d’expressions algébriques
- exemples en plusieurs parties d’expressions algébriques
exemples D’Expressions algébriques de base
exemple 1: écrire une expression algébrique pour la phrase mathématique ” la somme d’un nombre et de quatre”.
Solution: le mot « somme” nous donne immédiatement l’indice que nous allons ajouter ici. Notez que nous voulons ajouter deux quantités: un nombre inconnu et le nombre 4. Comme nous ne savons pas quelle est la valeur du nombre, nous pouvons utiliser une variable pour le représenter., Vous pouvez utiliser toutes les lettres de l’alphabet. Dans ce cas, convenons d’utiliser y pour la variable.
Lorsque nous ajoutons la variable y et 4, nous avons y + 4. Il est également correct d’écrire votre réponse comme 4 + y car l’addition est commutative – c’est-à-dire que changer l’ordre d’addition ne change pas sa somme.
La réponse finale est: y+4.
exemple 2: écrire une expression algébrique pour la phrase mathématique » 10 augmenté d’un nombre”.
Solution: les mots-clés « augmenté par » impliquent une addition. Cela signifie qu’un nombre inconnu a été ajouté à 10., En utilisant la lettre k comme variable, nous pouvons traduire l’instruction ci-dessus par 10 + K. puisque l’addition est commutative, nous pouvons la réécrire en k + 10. L’un des deux ci-dessus est une réponse correcte.
La réponse finale est k+10.
exemple 3: écrire une expression algébrique pour la phrase mathématique » la différence de 1 et un nombre”.
Solution: le mot « différence » suggère que nous allons soustraire. De plus, lorsque vous rencontrez ce mot mathématique (différence), assurez-vous de faire attention à l’ordre. Le numéro 1 vient en premier, puis un nombre inconnu vient en deuxième., Cela signifie que le numéro 1 est le minuend et le nombre inconnu est la soustraction. Si nous décidons d’utiliser la lettre x comme variable, la réponse devient 1-X.
la réponse finale est 1 – X.
exemple 4: écrivez une expression algébrique pour la phrase mathématique « un nombre inférieur à 8 ».
Solution: soyez très prudent lorsque vous traitez avec les mots-clés « moins que ». La première quantité qui précède les mots-clés « moins que » qui est ” un nombre » est le subtrahend. Alors que la quantité qui vient après devient la minuend.,
en d’autres termes, nous allons soustraire le nombre inconnu du nombre 8. Si nous choisissons notre variable pour être la lettre a, Nous obtenons 8-a.
la réponse finale est 8 – a.
exemple 5: écrivez une expression algébrique pour la phrase mathématique ” le produit de 5 et un nombre”.
Solution: pour trouver le produit de deux quantités ou valeurs, cela signifie que nous allons les multiplier ensemble. En sélectionnant la lettre m comme variable, l’expression algébrique de cette phrase mathématique est simplement 5m. cela signifie 5 fois le nombre inconnu M.
la réponse finale est 5m.,
exemple 6: écrire une expression algébrique pour la phrase mathématique « deux fois un nombre ».
Solution: le mot « deux fois » signifie que nous allons doubler quelque chose. Dans ce cas, nous voulons doubler une valeur ou une quantité inconnue. Soit la lettre d le nombre inconnu, quand on le double on obtient l’expression algébrique 2d.
la réponse finale est 2d.
exemple 7: écrire une expression algébrique pour la phrase mathématique « le quotient d’un nombre et 7 ».
Solution: le mot-clé « quotient » signifie que nous effectuons l’opération de division. Nous diviserons un nombre inconnu par 7., En choisissant la lettre w comme variable, la phrase mathématique ci-dessus peut être exprimée comme l’expression algébrique ci-dessous.
\LARGE{w \over 7}
exemple 8: écrire une expression algébrique pour la phrase mathématique ” le rapport de 10 et un nombre”.
Solution: de même, le mot « ratio » signifie division. L’ordre ici est très important. La première quantité est le nombre de 10 et la deuxième quantité est le nombre inconnu. Cela signifie que 10 est divisé par un nombre inconnu., Soit c le nombre inconnu, l’expression algébrique pour la phrase mathématique ci-dessus peut être écrite comme
\LARGE{10 \over c}
exemples D’Expressions algébriques en plusieurs parties
Cette fois, nous allons traiter des phrases mathématiques un peu plus complexes. Les expressions algébriques ici peuvent contenir deux opérations ou plus. Les mots-clés de base que nous apprenons auparavant serviront de base lorsque nous travaillerons avec les phrases mathématiques les plus difficiles à interpréter en expressions algébriques.,
exemple 1: écrire une expression algébrique pour la phrase mathématique ” 3 plus de deux fois un nombre ».
Solution: pour rendre cela beaucoup plus facile à comprendre, nous allons diviser cette phrase en deux parties. Tout d’abord, reconnaissez que nous avons un nombre inconnu. Nous pouvons le représenter par toutes les lettres de l’alphabet. Laissez le nombre inconnu être la variable X. Le diagramme ci-dessous devrait nous aider à voir ce qui se passe vraiment.,
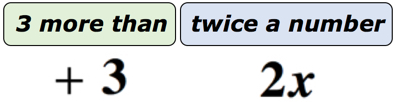
Si vous pensez à ce sujet, il y a un nombre inconnu représenté par la variable x qui est doublé ou multiplié par 2. Quel que soit le produit, nous y ajouterons 3. Donc, notre réponse finale devrait ressembler à celle ci-dessous.
La réponse finale est 2x+3.
exemple 2: écrivez une expression algébrique pour la phrase mathématique « la différence d’un demi-nombre et de 10 ».
Solution: supposons que la variable y soit le nombre inconnu., Le mot-clé « différence » nous indique que nous allons effectuer une soustraction. Il est crucial ici que nous fassions attention à l’ordre de soustraction. Après le mot « différence”, nous devrions nous attendre à deux quantités. Le premier sera le minuend, tandis que le second sera le subtrahend. Jetez un oeil au diagramme ci-dessous.
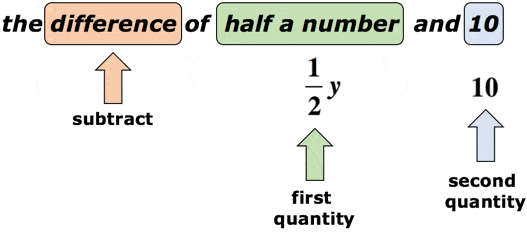
en se Référant au schéma ci-dessus, nous allons soustraire la première quantité par la seconde quantité. En d’autres termes, la deuxième quantité est soustraite de la première quantité., La réponse définitive pour les mathématiques phrase voudrais quelque chose comme ça,
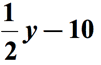
Exemple 3: Écriture d’une expression algébrique pour la formule mathématique « 7 de moins que le produit d’un nombre par 6 ».
Solution: nous savons que « moins que » suggère une opération de soustraction. Mais nous devons être un peu prudents ici parce que l’ordre sur la façon dont nous soustrayons est important. Supposons que le nombre inconnu soit représenté par la variable K. mettons cela sur un diagramme pour en avoir un sens. ,
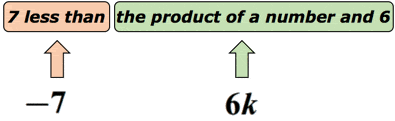
en Fait, cette formule mathématique peut être réécrite sous la forme
” le produit d’un nombre par 6 moins la 7 «
Le « 7 de moins que” signifie « moins de 7” à la quantité d’eau que d’être décrits, qui dans ce cas « le produit d’un nombre par 6”. Voici l’interprétation finale de la phrase mathématique dans une expression algébrique:
6k-7
exemple 4: écrivez une expression algébrique pour la phrase mathématique « la moyenne d’un nombre et 4 ».,
Solution: pour commencer sur cette phrase mathématique particulière, nous devons revoir ce que signifie le mot « moyenne”. Pour calculer la moyenne de deux chiffres ou plus, il faudra ajouter tous les nombres pour obtenir une somme puis de le diviser par le nombre d’entrées ou combien de numéros. Si nous laissons m être la variable pour représenter le nombre inconnu, la phrase mathématique ci-dessus peut être exprimée en expressions algébriques comme,
\LARGE{{m + 4} \over 2}
exemple 5: écrire une expression algébrique pour la phrase mathématique ” le quotient de 1, et 1 diminué d’un nombre”.,
Solution: le mot-clé « quotient » signifie que nous allons diviser. Dans ce cas, nous voulons diviser le nombre 1 par la quantité 1 diminuée d’un nombre. Voici l’expression algébrique qui peut représenter la phrase mathématique ci-dessus. Soit a le nombre inconnu.
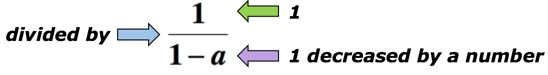
Exemple 6: Écriture d’une expression algébrique pour le calcul de la phrase « un tiers de le carré d’un nombre, a augmenté de 2 ».
Solution: il y a quelques choses qui se passent ici., Premièrement, la partie de la phrase qui dit ” un tiers du carré d’un nombre ” peut être interprétée comme ” le carré d’un nombre divisé par 3 « . Nous devrons augmenter le nombre inconnu par 2 puis diviser par 3. Supposons que le nombre inconnu est t, nous obtenons
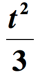
Nous ne sommes pas encore fait. La dernière étape consiste à ajouter la quantité ci-dessus de 2 pour incorporer la partie restante de l’expression ” augmenté de 2 « . Voici donc la représentation finale de la phrase mathématique donnée.,
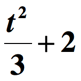
You might also be interested in:
Algebraic Expressions
Algebraic Sentences Word Problems