Lineaarinen Approksimaatio
oletetaan, että jonain päivänä olet unohtanut laskin ja todella haluat löytää miten neliöjuuri 2 on. Miten saisimme sen selville ilman laskinta? Voimme käyttää lineaarista approksimaatiota!
Linearisointi toiminto
linearisointi toiminto on vain noin löytää tangentin funktion tietyssä vaiheessa eri tavalla., Sen linearisointi kaava on:

missä L(x) on yhtälön tangentin pisteessä.
Miten tämä on meille hyötyä? No, voimme todella käyttää tätä yhtälöä vastaavan funktion arvoja lähellä kohta. Katso tämä kaavio.,
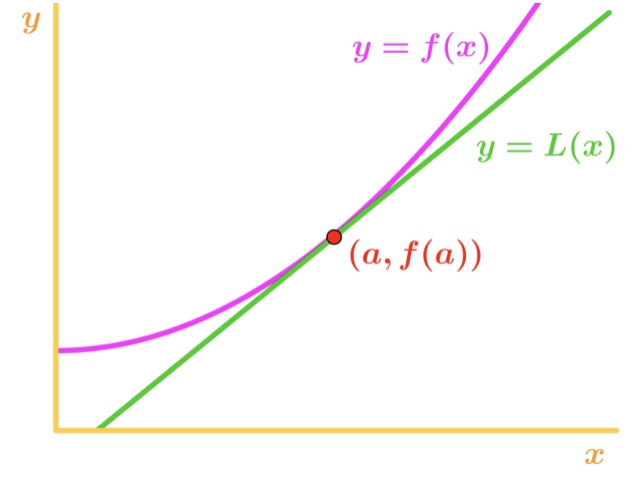
Huomaa, että x-arvot lähellä vaiheessa, voimme nähdä, että toiminta ja tangentin on suhteellisen lähellä toisiaan. Koska tämä, voimme kirjoittaa, että toiminto on suunnilleen yhtä suuri kuin tangentin lähellä kohta., Toisin sanoen,

missä ≈\n≈ on noin symboli. Tämä yhtälö tunnetaan lineaarisena approksimaatiokaavana. Se on lineaarinen siinä mielessä, että tangentti on suora viiva ja käytämme sitä likimääräisen funktion. Tällä approksimaatiolla voimme lähentää arvoja, joita ei voida tehdä käsin. Esimerkiksi neliöjuuri 2 tai luonnollinen log 5 voidaan approksimoida!, Yksi tärkeä asia huomata on, että tämä approksimaatio toimii vain x arvot lähellä kohta. Jos sinulla on x-arvo kaukana piste a, niin lainsäädännön tulee todella epätarkkoja.
älä Nyt tarkastelemme muutamia esimerkkejä löytää linearisointi toiminto, ja sitten katsoa, miten käyttää lineaarinen approksimaatio!
Etsi linearisointi L(x) funktion klo
Kysymys 1: Harkitse toiminto
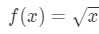
oletetaan, että haluamme löytää linearisointi funktion pisteessä a=4.
löytää linearisointi L(x), muista, että

- Vaihe 1: Etsi
- Vaihe 2: Etsi f(a)
- Vaihe 3: Etsi f'(a).
- Vaihe 4: Kytke kaikki kolme kaavaa löytää L(x)
-
nyt seuraa näitä ohjeita!,
Vaihe 1: onneksi a = 4 annetaan meille kysymyksessä, joten meidän ei tarvitse etsiä sitä.
- Vaihe 2:
Huomaa, että
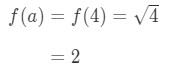
Yhtälö 1: Linearisointi kysymys pt. 3 - Vaihe 3:
Tiedä, että johdannainen square juuret on
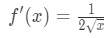
Yhtälö 1: Linearisointi kysymys pt., 4 And so plugging in x=a gives us:
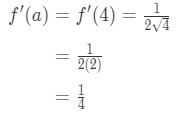
Equation 1: Linearization question pt. 5 - Step 4:
Since we know a, f(a), and f'(a), we can now plug it into L(x) to find the linearization of f(x).
Hence,
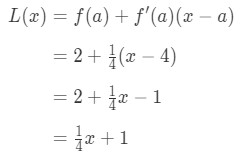
Equation 1: Linearization question pt., 6 Niin L(x)=14\frac{1}{4}41x+1 on linearisointi tämä toiminto pisteessä x=4. Lisäksi se on myös funktion tangenttiviiva pisteessä x=4.
Miten lineaarinen approksimaatio
Muista aiemmin sanoimme, että voimme käyttää yhtälö ja tangentin lähentää arvot funktion lähellä? Kokeillaan tätä aiemmin löytämällämme linearisaatiolla. Muista, että
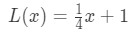
pistettä lähellä x=4. Voimme muuttaa tätä lineaarinen approksimaatio f(x) sanomalla, että:
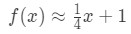
Nyt, sanotaanko haluan lähentää f(4.04). Jos tämä kytkettäisiin alkuperäiseen funktioon, saisit 4.04\sqrt{4.04}4.04 . Tätä olisi todella vaikea laskea ilman laskinta., Kuitenkin, käyttäen lineaarinen approksimaatio, voimme sanoa, että

Nyt toistaiseksi näihin kysymyksiin antoi meille toiminto ja kohta töihin. Entä jos näitä ei anneta lainkaan? Entä jos kysymys käskee vain arvioimaan numeron?
Käytä Lineaarinen approksimaatio arvioida numero
Oletetaan, että haluamme arvioida 10\sqrt{10}10. Miten me sen tekisimme?, Meillä olisi tarve käyttää lineaarinen approksimaatio

mutta meillä ei ole edes toiminto ja kohta töihin. Tämä tarkoittaa, että meidän on tehtävä ne itse. Tämä johtaa meidät tekemään seuraavat vaiheet:
- Vaihe 1: luo toiminto
- Vaihe 2: luo-a alakohta
- Vaihe 3: Etsi f(a) ja f'(a)
- Vaihe 4: Kytke kaikkemme lineaarinen approksimaatio formula
seuraa ohjeita!,
Kysymys 2: Arvio 10\sqrt{10}10
- Vaihe 1: katsotaanpa keksiä toiminto. Huomaa, että olemme arvioimalla
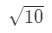
Yhtälö 3: Arvio lineaarinen noin. pt.2 Meidän täytyy jotenkin tehdä suhde f(x) ja 10\sqrt{10}10. Emme voi sanoa, että f(x) = 10\sqrt{10}10, koska toiminta ei ole riippuvainen x. Joten miksi emme tee tätä? Anna
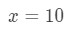
Yhtälö 3: Arvio lineaarinen noin. pt.,3 Jos me teemme sen, me pohjimmiltaan sanoa
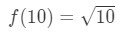
Yhtälö 3: Arvio lineaarinen noin. pt.4 Voimme nyt ilmeisesti kertoa, mitä funktion pitäisi olla. Anna
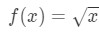
Yhtälö 3: Arvio lineaarinen noin. pt.5 Joten meillä on toiminto, mutta nyt meidän täytyy kohta on työskennellä.,
- Vaihe 2:
avain löytää oikea arvo on, ottamalla huomioon kaksi asiaa:
1) varmista, että arvo on lähellä x
2) varmista, että f(a) on mukava määrä.
riittääkö a = 8? No, 8 on aika lähellä 10, joten se ei ole huono. Kuitenkin,
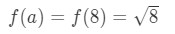
Yhtälö 3: Arvio lineaarinen noin. pt.6 Huomaa, että 8\sqrt{8}8 ei ole kovin mukava määrä. Itse asiassa, saat kasan desimaalilukuja. Meidän on kokeiltava jotain muuta.,
riittääkö a = 9? Jälleen, 9 on melko lähellä 10 joten se on OK. Myös,

Yhtälö 3: Arvio lineaarinen noin. pt.7 f(a) on todella mukava koko numero täällä, joten tämä todella toimii! Joten poiminta a = 9 riittää.
- Vaihe 3:
Huomaa, että aiemmin:

Yhtälö 3: Arvio lineaarinen noin. pt.,8 Calculating f'(x) we have again:

Equation 3: Estimate with linear approx. pt.9 So
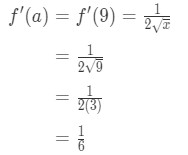
Equation 3: Estimate with linear approx. pt.,10 - Step 4:
Going back to the linear approximation formula we have:

Equation 3: Estimate with linear approx. pt.11 Plugging a, f(a), f'(a), f(x), and x in our formula you will see that:

Equation 3: Estimate with linear approx. pt.12 Hence, we just approximated the number!,
Jos haluat enemmän käytännön ongelmia, lineaarinen approksimaatio, niin suosittelen katsomaan tämän linkin tänne.
http://tutorial.math.lamar.edu/Classes/CalcI/LinearApproximations.aspx
Yliarvioida eikä Aliarvioida
Me tiedämme, että lineaarinen approksimaatio on vain arvio funktion arvo tietyssä kohdassa. Mutta mistä tiedämme, että jos arviomme on yliarvioitu tai aliarvioitu? Lasketaan toinen derivaatta ja katsotaan concavity.,
Kovera ylös vs Kovera alas
Jos toinen derivaatta on suurempi kuin 0 arvot lähellä, sitten toiminto on kovera ylös. Tämä tarkoittaa, että lähentymisemme on aliarvioitu. Toisin sanoen,
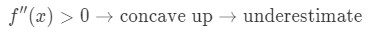
Miksi? Katsotaanpa tätä kaaviota.,
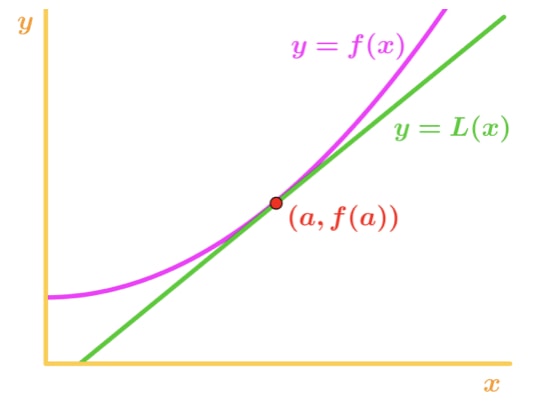
Huomaa, että f(x) on kovera ylöspäin ja tangentin on oikeassa nojalla f(x). Sanotaan oli käyttää tangentti linja likimääräinen f (x). Silloin tangenttiviivan y-arvot jäävät aina pienemmiksi kuin F: n(x) todellinen arvo. Näin ollen meillä on aliarvioida
Nyt, jos toinen derivaatta on pienempi kuin 0-arvot lähellä, sitten toiminto on kovera alas., Tämä tarkoittaa, että lähentymisemme on yliarvioitu. Toisin sanoen,
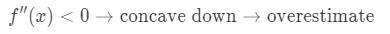
Jälleen, miksi? Katsotaanpa toista graafia.
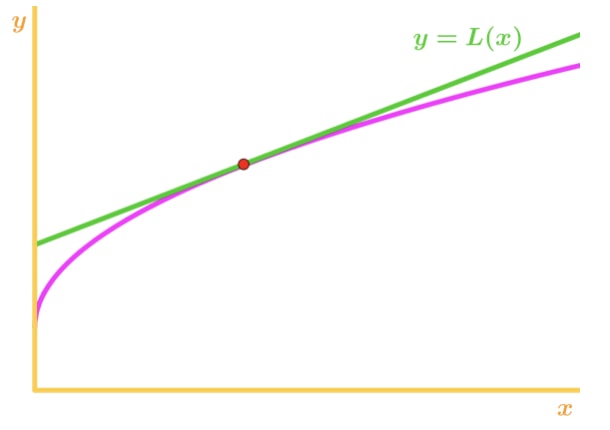
Huomaa, että f(x) on alaspäin kovera ja tangentin on oikeus edellä f(x). Jälleen, sanotaan, että aiomme käyttää tangentti linja likimääräinen f (x)., Silloin tangenttiviivan y-arvot tulevat aina olemaan suurempia kuin F: n(x) todellinen arvo. Siksi olemme yliarvioineet.
jos haluat nähdä, jos arvo on aliarvioimiseen tai yliarviointi, varmista, että noudatat näitä ohjeita:
- Vaihe 1: Etsi toinen derivaatta
- Vaihe 2: katso sivujen toiminta lähellä a alakohta
- Vaihe 3: Vahvistaa, että se on aliarvioida/yliarvioida
katsotaanpa katsomaan esimerkki:
3. Kysymys: Olkoon f(x) = x – \sqrt{x}x ja a = 4. Jos me lineaarinen likimääräinen f (4.,04), olisiko se yliarvioimista vai aliarvioimista?
- Vaihe 1: Katso, että
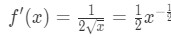
Yhtälö 4: Yliarvioida kysymys pt.1 Eli toinen derivaatta on
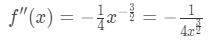
Yhtälö 4: Yliarvioida kysymys pt.2 - Vaihe 2:
Huomaa, että a=4, joten haluamme katsoa positiiviset x: n arvot lähellä 4. Katso nyt toista johdannaista., Kun x on positiivinen, me näemme, että
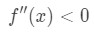
Yhtälö 4: Yliarvioida kysymys pt.3 Näin ollen, se on kovera alas
- Vaihe 3:
Me tiedämme, että jos toiminto on kovera alas, sitten tangentin yläpuolella toiminto. Näin ollen käyttämällä tangentti linja lähentämisestä antaa yliarvioitu arvo.
Erot
Ei vain voimme likimääräisiä arvoja, lineaarinen approksimaatio, mutta voimme myös arvioitu, jossa erot., Lähentää, käytämme seuraavaa kaavaa
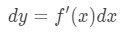
missä dy ja dx on eroja, ja f'(x) on johdannainen f suhteen x. Koska olemme tekemisissä hyvin pieniä muutoksia vuonna x ja y, niin aiomme käyttää siihen, että:
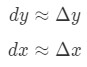
Kuitenkin suurin osa kysymyksistä, emme liity asetus
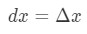
Joten käyttämällä näitä tosiasiat johtavat meidät on:
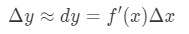
Tämä lähentäminen on erittäin hyödyllinen, kun lähentämällä muutos y., Pidä mielessä, silloin heillä ei ollut laskimia, joten tämä on paras lähentämisestä he voisivat saada toiminnot neliöjuuria tai luonnon lokit.
suurimman osan ajasta joudut etsimään F'(x) ja Δ\Deltaδx itse. Toisin sanoen, noudata näitä ohjeita likimääräinen Δ\DeltaΔy!
- Vaihe 1: Etsi Δ\DeltaΔx
- Vaihe 2: Etsi f'(x)
- Vaihe 3: Kytke kaikki kaavaan löytää dy. dy on likiarvo Δ\DeltaΔy.
katsotaanpa esimerkki käyttää tätä lähentämistä:
Kysymys 4: tarkastellaan funktiota y = ln(x + 1)., Oletetaan, että x muuttuu 0: sta 0.01: een. Likimääräinen Δ\Deltaδy.
- Vaihe 1: Huomaa, että x-muutokset 0, 0,01, joten muutos x olisi:
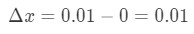
Yhtälö 6: Differential kysymys pt.1 - Vaihe 2:
johdannainen voisi olla:
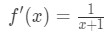
Yhtälö 6: Differential kysymys pt.,2 - Vaihe 3:
Kytkemällä kaikki, mitä meillä on:
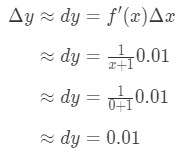
Yhtälö 6: Differential kysymys pt.3 Näin ollen Δ\DeltaΔy ≈\n≈ 0.01
Kuitenkin, suurimman osan ajasta emme halua arvioida arvo toiminto, ja ei muuta arvoa. Näin ollen meidän tulee lisätä molemmin puolin yhtälöstä y, joka antaa meille:
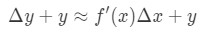
joka on sama kuin:
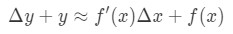
Tämä yhtälö on erittäin vaikea lukea, joten aiomme järjestää sitä vielä enemmän. Yritetään päästä eroon Y ja Δ\deltaδy. Huomaa, että Δ\DeltaΔy+ y on periaatteessa sama kuin löytää arvo funktion Δ\DeltaΔx+x. Toisin sanoen,
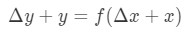
Näin ollen sijoittamalla tämä meidän lähentämisestä edellä antaa meille:
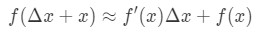
missä f(Δ\DeltaΔx+x) on arvo, me yritämme arvioida. Miten tätä kaavaa käytetään? Suosittelen seuraavia ohjeita:
käytetään näitä ohjeita seuraavaan kysymykseen.
kysymys 5: Käytä differentiaaleja likimäärin 10\sqrt{10}10.
- Vaihe 1: Vertaile f(Δ\DeltaΔx+x) 10\sqrt{10}10., Since 10\sqrt{10}10 has a square root and 9 is a perfect square that is closest to 10, then let
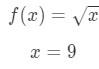
Equation 7: Approximate value with differentials pt.1 Notice that:
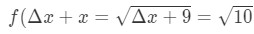
Equation 7: Approximate value with differentials pt.,2 Nähdä, että ei ole valinta mutta antaa Δ\DeltaΔx = 1
- Vaihe 2:
Katso, että johdannainen antaa:

Yhtälö 7: Arvioitu arvo erot pt.3 tämä merkitsee,
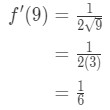
Yhtälö 7: Arvioitu arvo erot pt.,4 - Vaihe 3:
Kytkemällä kaikki osaksi kaava antaa meille:
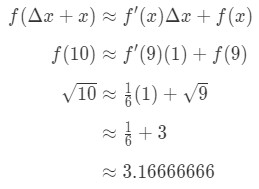
Yhtälö 7: Arvioitu arvo erot pt.5 Näin ollen meidän on vain arvioitu määrä.
Yksi mielenkiintoinen asia huomata on, että lineaarinen approksimaatio ja erot sekä antaa sama tulos 10\sqrt{10}10.,
Jos haluat oppia lisää erot, klikkaa tätä linkkiä:
http://tutorial.math.lamar.edu/Classes/CalcI/LinearApproximations.aspx
Todistaa L’Hospital Sääntöä käyttäen lineaarinen approksimaatio
– Nyt olemme oppineet paljon siitä, lineaarinen approksimaatio, mutta mitä muuta voimme tehdä? Voimme itse asiassa käyttää lineaarista approksimaatiokaavaa todistaaksemme säännön, joka tunnetaan nimellä L ’Hospital’ s Rule . Näin todisteet toimivat.
Muista, että lineaarinen likiarvo kaava on:

Katso, että voimme muuttaa kaava siten, että:
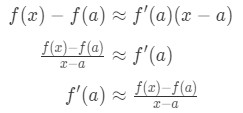
Ymmärtää, että lainsäädännön tulee enemmän ja enemmän tarkka kuin me poimia x-arvot, jotka ovat lähempänä. Toisin sanoen, jos me otamme raja-arvo, kun x→a, niin ne ovat tasa-arvoisia. Niin,
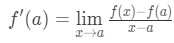
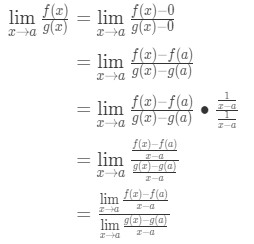
Nyt huomaa, että voimme soveltaa kaava, että me johdettu aiemmin täällä. Joten nyt
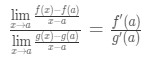
Nyt kirjoittamisen sijaan f'(a) ja g'(a), voimme soveltaa rajoja, kun x→a (koska me tiedämme, f ja g on derivoituva)., Niin,
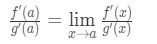
Näin ollen, olemme juuri osoitti että:
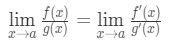
joka on L’Hospital on Sääntö .
milloin käytetään l ’hopitalin sääntöä
haluamme aina soveltaa l’ hoptialin sääntöä, kun kohtaamme epämääräisiä rajoja. Epämääräisiä muotoja on kahdenlaisia., Nämä määrittämättömät lomakkeet olisi:
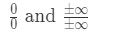
monet ihmiset tekevät virheen käyttämällä l ’ hopital sääntö ilman edes tarkistaa, jos se on epämääräinen raja. Tarkista siis ensin! Muuten se ei toimi ja saat väärän vastauksen. Tässä on opas käyttämällä l ’ hopital sääntö:
- Vaihe 1: Arvioi raja suoraan.
- Vaihe 2: Tarkista, onko se yksi epämääräisistä muodoista. Jos on, siirry vaiheeseen 3.,
- Vaihe 3: Käytä l ’ hopitalin sääntöä.
- Vaihe 4: Tarkista, saatko toisen epämääräisen lomakkeen. Toista vaihe 3, Jos teet niin.
Katsotaanpa muutamia esimerkkejä näiden vaiheiden avulla.
Kysymykseen 6: Arvioi raja –
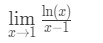
- Vaihe 1: Arvioidaan raja suoraan antaa meille
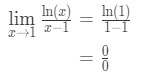
Yhtälö 9: L ’ hopital sääntö kysymys pt.,2 - Vaihe 2:
Kyllä, se on yksi epämääräinen muotoja.
- Vaihe 3:
Hakeminen l ’ hopital sääntö meillä on:
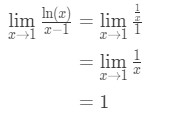
Yhtälö 9: L ’ hopital sääntö kysymys pt.3 - Vaihe 4:
yksi ei ole määräämättömäksi muodossa, joten olemme tehneet ja vastaus on 1.
nyt tuo kysymys oli vähän helppo, joten miksi emme katso jotain vähän kovempaa.,
Kysymykseen 7: Arvioi raja –
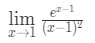
- Vaihe 1: Arvioidaan raja suoraan näemme, että:
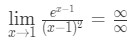
Yhtälö 10: L ’ hopital sääntö kahdesti kysymys pt.2 - Vaihe 2:
Tämä on määrittelemätön muoto, niin siirry vaiheeseen 3.,
- Vaihe 3:
Hakeminen l ’ hopital sääntö meillä on,
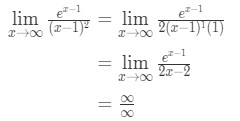
Yhtälö 10: L ’ hopital sääntö kahdesti kysymys pt.3 - Vaihe 4:
Tämä on toinen epämääräinen muodossa. Meidän on palattava vaiheeseen 3 ja sovellettava taas l ’ hoptialin sääntöjä.
- Vaihe 3:
Hakeminen l ’ hopital sääntö taas meillä on:
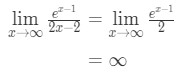
Yhtälö 10: L ’ hopital sääntö kahdesti kysymys pt.,4 - Vaihe 4:
Infinity ei ole määräämättömäksi muodossa, joten olemme tehneet ja vastaus on ääretön\infty∞: lle