Angenommen, Sie möchten die Auswirkungen eines Risikofaktors auf die Zeit bis zum Auftreten eines Ereignisses berücksichtigen. Zum Beispiel betrachten Arnlov et al (2010) die Auswirkungen des Body-Mass-Index (BMI) und des metabolischen Syndroms auf die Entwicklung von Herz-Kreislauf-Erkrankungen und den Tod bei Männern mittleren Alters. Die Assoziationen wurden anhand von Daten aus einer Kohortenstudie von 1758 schwedischen Männern mittleren Alters mit Wohnsitz in einem Landkreis mit über 30-jähriger Nachbeobachtung untersucht., Die folgende Abbildung zeigt die Zeit bis zu einem kardiovaskulären Großereignis nach BMI-Kategorie und Vorhandensein (B) oder Fehlen (A) des metabolischen Syndroms. Gibt es einen Unterschied in diesen Überlebenskurven?

Abbildung 2: Kaplan-Meier-Kurven für kardiovaskuläre Großereignisse in verschiedenen BMI-Kategorien bei Personen ohne MetS (A) und mit MetS (B).

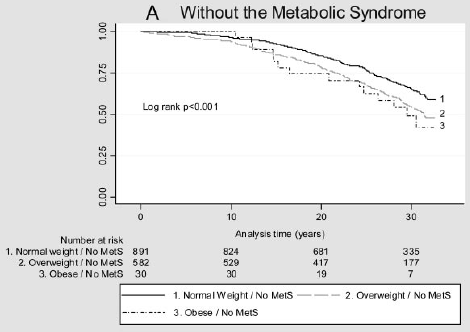
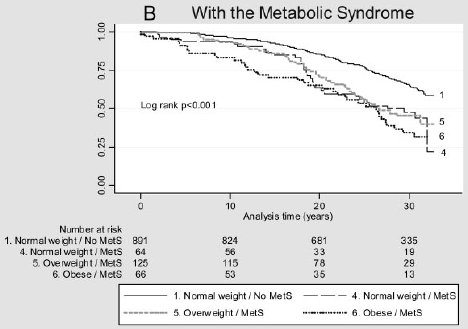
(Abbildungen aus Arnlov, J et al., Auswirkungen des Body-Mass-Index und des metabolischen Syndroms auf das Risiko von Herz-Kreislauf-Erkrankungen und Tod bei Männern mittleren Alters. Circulation 2010; 121; 230-236, ursprünglich online veröffentlicht 12/28/2009; DOI 10.1161/CIRCULATIONAHA.109.88752)

Das Auftreten eines großen kardiovaskulären Ereignisses ist eine binäre Antwort. Wäre eine logistische Regression mit BMI als Prädiktorvariable geeignet, um diese Daten zu analysieren?,

Answer

Die Beziehung zwischen dem Vorhandensein oder Fehlen eines großen kardiovaskulären Ereignisses und der Prädiktorvariablen könnte zu einem bestimmten Zeitpunkt mit der logistischen Regression beurteilt werden, dies würde jedoch die Überlebenskurven nicht direkt vergleichen. Eine Überlebensanalyse würde die Kurven anhand der Zeit mit dem Ereignis vergleichen.

Überlebensanalysemethoden wie die proportionale Risikoregression unterscheiden sich von der logistischen Regression durch die Bewertung einer Rate anstelle eines Anteils.,

Proportional hazards Regression Auch Cox-Regression genannt, modelliert die Inzidenz oder Gefährdungsrate, die Anzahl der neuen Krankheitsfälle pro Risikopopopulation pro Zeiteinheit. Wenn das Ergebnis der Tod ist, ist dies die Sterblichkeitsrate.
Gefahrenfunktion Die Gefahrenfunktion ist die Wahrscheinlichkeit, dass eine Person, die bis t überlebt, das Ereignis im nächsten Moment erfährt.

Die logistische Regression berücksichtigt dagegen den Anteil neuer Fälle, die sich in einem bestimmten Zeitraum entwickeln, d. H. Die kumulative Inzidenz., Logistische Regression schätzt das odds ratio; proportional hazards Regression schätzt das Hazard Ratio.

Das Verhältnis der Gefahrenfunktionen kann als Verhältnis der Risikofunktionen betrachtet werden, so dass das proportionale Risikoregressionsmodell als Funktion des relativen Risikos betrachtet werden kann (während logistische Regressionsmodelle eine Funktion eines Odds Ratio sind). Veränderungen in einer Kovariate haben einen multiplikativen Effekt auf das Basisrisiko. Das Modell in Bezug auf die hazard-Funktion zum Zeitpunkt t ist:

– \(\lambda \left ( t|X_{1i},X_{2i},…,X_{Ki} \right )=\lambda_{0} (t)exp\left ( \beta_{1}X_{1i}+\beta_{2}X_{2i}+…,+ \ beta_{K}X_{Ki} \right )\)

Obwohl kein bestimmtes Wahrscheinlichkeitsmodell ausgewählt ist, um die Überlebenszeiten darzustellen, hat die proportionale Gefahren-Regression eine wichtige Annahme: Die Gefahr für jede Person ist ein fester Anteil der Gefahr für jede andere Person. (d. h. proportionale Gefahren)., Beachten Sie, wenn \(\lambda_0 (t)\) die Gefahrenfunktion für ein Subjekt mit allen Prädiktorwerten gleich Null und \(\lambda_1 (t)\) die Gefahrenfunktion für ein Subjekt mit anderen Werten für die Prädiktorvariablen ist, hängt das Gefahrenverhältnis nur von den Prädiktorvariablen ab und nicht von der Zeit t. Diese Annahme bedeutet, dass, wenn eine Kovariate das Risiko des Ereignisses am ersten Tag verdoppelt, auch das Risiko des Ereignisses an einem anderen Tag verdoppelt wird. ,

Proportionale Gefährdungsmodelle können für diskrete oder kontinuierliche Messungen der Ereigniszeit verwendet werden und können zeitabhängige Kovariaten (Kovariaten, deren Werte sich während des Beobachtungszeitraums ändern können) enthalten. Mithilfe der proportionalen Hazards Regression können kovariat angepasste Hazard (oder Risk) Verhältnisse erzeugt werden.

Kehren wir zur ursprünglichen Frage von Arnlov und zurück colleagues…do BMI und metabolisches Syndrom beeinflussen die Entwicklung von Herz-Kreislauf-Erkrankungen? Lesen Sie die Arnlov et al., Auswirkungen des Body-Mass-Index und des metabolischen Syndroms auf das Risiko von Herz-Kreislauf-Erkrankungen und Tod bei Männern mittleren Alters, 2010;121;230-236, wobei den statistischen Methoden, Ergebnissen und Schlussfolgerungen besondere Aufmerksamkeit geschenkt wird.

Vergleichen und kontrastieren Sie den proportionalen logistischen Regressionsansatz mit einem logistischen Regressionsansatz, indem Sie Franco et al. Trajektorien des Eintritts in das metabolische Syndrom: Die Framingham Heart Study. Auflage 2009; 120; 1943-1950; ursprünglich online veröffentlicht 2. November 2009; American Heart Association. 7272 Greenville Avenue, Dallas, Texas DOI: 10.,1161/CIRCULATIONAHA.109.855817

Sie können auch die Ergebnisse der beiden Studien vergleichen. Beide Papiere befinden sich in der Lesungen Ordner für Woche 14.

Hinweis! Wenn Sie mit Kaplan-Meier-Kurven nicht vertraut sind, lesen Sie das Kapitel Überlebensanalyse in den Monographien Research Methods II des Journal of Tropical Pediatrics

(Zugriff über http://www.oxfordjournals.org/our_journals/tropej/online/ma_chap12.pdf)