Nach Radius und Durchmesser ist ein weiterer wichtiger Teil eines Kreises ein Bogen. In diesem Artikel werden wir ausführlich besprechen, was ein Bogen ist, wie man die Länge eines Bogens und die Messung einer Bogenlänge im Bogenmaß findet. Wir werden auch über den kleinen Bogen und den großen Bogen studieren.
Was ist ein Kreisbogen?
Ein Kreisbogen ist ein beliebiger Teil des Umfangs eines Kreises. Um sich zu erinnern, ist der Umfang eines Kreises der Umfang oder die Entfernung um einen Kreis., Daher können wir sagen, dass der Umfang eines Kreises der volle Bogen des Kreises selbst ist.
Wie finde ich die Länge eines Bogens?
Die Formel zur Berechnung des Bogens besagt, dass:
Bogenlänge = 2nr (θ/360)
Wobei r = der Radius des Kreises,
π = pi = 3.14
θ = der Winkel (in Grad), der durch einen Bogen in der Mitte des Kreises subtendiert wird.
360 = der Winkel einer kompletten Drehung.
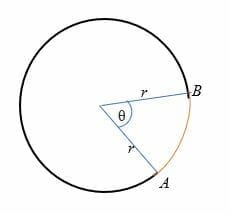
Aus der obigen Abbildung ist die Länge des Bogens (rot gezeichnet) der Abstand von Punkt A zu Punkt B.,
Lassen Sie uns ein paar Beispielprobleme über die Länge eines Bogens ausarbeiten:
Beispiel 1
Wenn der Bogen einen Winkel von 40 Grad zum Mittelpunkt eines Kreises mit einem Radius von 7 cm anhält. Berechnen Sie die Länge des Bogens AB.
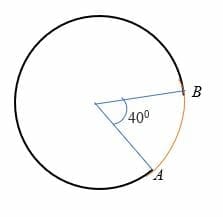
Lösung
Gegeben r = 7 cm
θ = 40 Grad.
Durch substitution,
Die Länge eines Bogens = 2nr(θ/360)
Länge = 2 x 3,14 x 7 x 40/360
= 4.884 cm.
Beispiel 2
Ermitteln Sie die Länge eines Kreisbogens, der einen Winkel von 120 Grad zum Mittelpunkt eines Kreises mit einem Radius von 24 cm angibt.,
Lösung
Die Länge eines Bogens = 2nr(θ/360)
= 2 x 3,14 x 24 x 120/360
= 50.24 cm.
Beispiel 3
Die Länge eines Bogens beträgt 35 m. Wenn der Radius des Kreises 14 m beträgt, ermitteln Sie den Winkel, der vom Bogen subtendiert wird.
Lösung
Die Länge eines Bogens = 2nr(θ/360)
35 m = 2 x 3,14 x 14 x (θ/360)
35 = 87.92 θ/360
Multiplizieren Sie beide Seiten mit 360 zu entfernen, die den Bruch.
12600 = 87.92 θ
Teilen Sie beide Seiten durch 87.92
θ = – Grad-143.3.,
Beispiel 4
Ermitteln Sie den Radius eines Bogens mit einer Länge von 156 cm und einem Winkel von 150 Grad zum Mittelpunkt eines Kreises.
Lösung
Die Länge eines Bogens = 2nr(θ/360)
156 cm = 2 x 3,14 x r x 150/360
156 = 2.6167 r
Teilen Sie beide Seiten durch 2.6167
r = 59.62 cm.
Der Radius des Bogens beträgt also 59,62 cm.
Wie finde ich die Bogenlänge im Bogenmaß?
Es besteht eine Beziehung zwischen dem Winkel, der durch einen Bogen im Bogenmaß subtendiert wird, und dem Verhältnis der Länge des Bogens zum Radius des Kreises., In diesem Fall
θ = (die Länge eines Bogens) / (der Radius des Kreises).
Daher ist die Länge des Bogens im Bogenmaß gegeben durch,
S = r θ
wobei θ = Winkel, der von einem Bogen im Bogenmaß
S = Länge des Bogens.
r = radius des Kreises.
Ein Radian ist der zentrale Winkel, der durch eine Bogenlänge von einem Radius subtendiert wird, dh s = r
Der Radian ist nur eine andere Möglichkeit, die Größe eines Winkels zu messen. Um beispielsweise Winkel von Grad in Bogenmaß umzuwandeln, multiplizieren Sie den Winkel (in Grad) mit π/180.,
Um den Bogenmaß in Grad umzuwandeln, multiplizieren Sie den Winkel (in Bogenmaß) mit 180 / π
Beispiel 5
Ermitteln Sie die Länge eines Bogens mit einem Radius von 10 cm und einem Winkel von 0, 349 Bogenmaß.
Lösung
Arc Länge = r θ
= 0.349 x 10
= 3.49 cm.
Beispiel 6
Ermitteln Sie die Länge eines Bogens im Bogenmaß, der einen Radius von 10 m und einen Winkel von 2.356 Bogenmaß hat.
Lösung
Bogenlänge = r θ
= 10 m x 2.356
= 23.56 m.
Beispiel 7
Finden Sie den Winkel, der von einem Bogen mit einer Länge von 10.05 mm und einem Radius von 8 mm subtendiert wird.,
Lösung
Arc Länge = r θ
10.05 = 8 θ
Teilen Sie beide Seiten durch 8.
1.2567 = θ
Dort beträgt der vom Bogen subtendierte Winkel 1.2567 Bogenmaß.
Beispiel 8
Berechnen Sie den Radius eines Kreises, dessen Bogenlänge 144 Yards und Bogenwinkel 3.665 Bogenmaß beträgt.
Lösung
Arc Länge = r θ
144 = 3.665 r
Teilen Sie beide Seiten durch 3.665.
144/3.665 = r
r = 39.29 Meter.
Beispiel 9
Berechnen Sie die Länge eines Bogens, der einen Winkel von 6,283 Bogenmaß zum Mittelpunkt eines Kreises mit einem Radius von 28 cm teilt.,
Lösung
Bogenlänge = r θ
= 28 x 6.283
= 175.93 cm
Kleiner Bogen (h3)
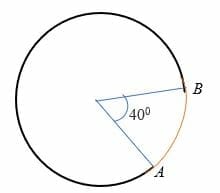
Der kleine Bogen ist ein Bogen, der einen Winkel von weniger als 180 Grad zum Mittelpunkt des Kreises unterlegt. Mit anderen Worten, der kleinere Bogen misst weniger als einen Halbkreis und wird auf dem Kreis durch zwei Punkte dargestellt. Zum Beispiel ist der Bogen AB im Kreis unten der kleinere Bogen.
Major arc (h3)
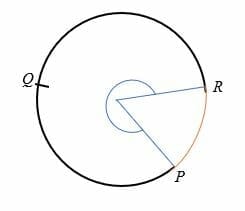
Der Hauptbogen eines Kreises ist ein Bogen, der einen Winkel von mehr als 180 Grad zum Mittelpunkt des Kreises subtendiert., Der Hauptbogen ist größer als der Halbkreis und wird durch drei Punkte auf einem Kreis dargestellt.
Zum Beispiel ist PQR der Hauptbogen des unten gezeigten Kreises.
Übungsprobleme
- Ermitteln Sie die Fläche des Kreissektors mit einem Radius von 9 mm. Nehmen Sie an, der Winkel, der von diesem Bogen in der Mitte subtendiert wird, beträgt 30 o.
- Stadt A liegt nördlich von Stadt B. Die Breiten von Stadt A und Stadt B betragen 54 o N bzw. Wie groß ist die Nord-Süd-Distanz zwischen den beiden Städten? Der Radius der Erde beträgt 6400 km.,