det finns ingen enda strategi för att översätta matematiska fraser till algebraiska uttryck. Så länge du kan komma ihåg grunderna, bör du kunna ta itu med de mer utmanande. Se bara till att du kan motivera hur du kommer upp med ditt eget algebraiska uttryck, och ännu viktigare att det är vettigt för dig. Be alltid om hjälp från dina lärare, efter behov eller samarbeta med dina klasskamrater så att du kan verifiera dina svar.,
för att bygga dina färdigheter i att skriva algebraiska uttryck, kommer vi att gå över olika sätt att hur varje operation kan dyka upp som ett ord eller en fras i problemet. De fyra aritmetiska operationerna är addition, subtraktion, multiplikation och division.,
Key Words for Addition

Key Words for Subtraction

Key Words for Multiplication

Key Words for Division

It is time now time to go over some examples to practice writing algebraic expressions., Jag separerar exemplen i två:
- grundläggande exempel på algebraiska uttryck
- flerdelade exempel på algebraiska uttryck
grundläggande algebraiska uttryck exempel
exempel 1: Skriv ett algebraiskt uttryck för matematikfrasen ”summan av ett tal och fyra”.
lösning: ordet ” sum ” ger oss omedelbart tipset som vi kommer att lägga till här. Lägg märke till att vi vill lägga till två kvantiteter: ett okänt nummer och nummer 4. Eftersom vi inte vet vad värdet av numret, kan vi använda en variabel för att representera den., Du kan använda alla bokstäver i alfabetet. I det här fallet, låt oss komma överens om att använda y för variabeln.
När vi lägger till variabeln y och 4 har vi y + 4. Det är också okej att skriva ditt svar som 4 + y eftersom tillägg är kommutativt-det vill säga att byta tilläggsorder ändrar inte summan.
det slutliga svaret är y+4.
exempel 2: Skriv ett algebraiskt uttryck för matematikfrasen ”10 ökat med ett tal”.
lösning: sökorden ”ökat med” innebär tillägg. Detta innebär att ett okänt nummer har lagts till 10., Med bokstaven k som variabeln kan vi översätta uttalandet ovan som 10 + k. eftersom tillägg är kommutativt kan vi skriva om det som k + 10. Någon av de två ovan är ett korrekt svar.
det slutliga svaret är K+10.
exempel 3: Skriv ett algebraiskt uttryck för matematikfrasen ”skillnaden mellan 1 och ett tal”.
lösning: ordet ”skillnad” tyder på att vi kommer att subtrahera. Dessutom, när du stöter på detta matematiska ord (skillnad) se till att uppmärksamma ordern. Nummer 1 kommer först då ett okänt nummer kommer i andra., Det betyder att nummer 1 är minuend och det okända numret är subtrahend. Om vi väljer att använda bokstaven x som vår variabel blir svaret 1-x.
det slutliga svaret är 1 – x.
exempel 4: Skriv ett algebraiskt uttryck för matematikfrasen ”ett tal mindre än 8”.
lösning: var mycket försiktig när du hanterar sökorden ”mindre än”. Den första kvantiteten som kommer före ”mindre än” nyckelord som är ”ett tal” är subtrahend. Medan den mängd som kommer efter det blir minuend.,
med andra ord kommer vi att subtrahera det okända numret från numret 8. Om vi väljer vår variabel att vara bokstaven a får vi 8-a.
det slutliga svaret är 8-a.
exempel 5: Skriv ett algebraiskt uttryck för matematikfrasen ”produkten av 5 och ett nummer”.
lösning: för att hitta produkten av två kvantiteter eller värden betyder det att vi kommer att multiplicera dem tillsammans. Att välja bokstaven m som vår variabel är det algebraiska uttrycket för denna matematiska fras helt enkelt 5m. det betyder 5 gånger det okända numret m.
det slutliga svaret är 5m.,
exempel 6: Skriv ett algebraiskt uttryck för matematikfrasen ”två gånger ett tal”.
lösning: ordet” två gånger ” betyder att vi kommer att dubbla något. I det här fallet vill vi dubbla ett okänt värde eller kvantitet. Låt bokstaven d vara det okända numret, när vi dubblar det får vi det algebraiska uttrycket 2d.
det slutliga svaret är 2d.
exempel 7: Skriv ett algebraiskt uttryck för matematikfrasen ”kvoten av ett nummer och 7”.
lösning: sökordet ”quotient” betyder att vi utför Divisionens funktion. Vi kommer att dela ett okänt nummer med 7., Att välja bokstaven w som vår variabel kan matematikfrasen ovan uttryckas som det algebraiska uttrycket nedan.
\LARGE{w \over 7}
exempel 8: Skriv ett algebraiskt uttryck för matematikfrasen ”förhållandet mellan 10 och ett tal”.
lösning: på samma sätt betyder ordet ”förhållande” uppdelning. Ordern här är mycket viktig. Den första kvantiteten är nummer 10 och den andra kvantiteten är det okända numret. Det betyder att 10 divideras med ett okänt nummer., Låt c vara det okända numret, det algebraiska uttrycket för matematikfrasen ovan kan skrivas som
\ LARGE{10 \ over c}
multi-Part algebraiska uttryck exempel
den här gången kommer vi att hantera matematiska fraser som är lite mer komplexa. De algebraiska uttrycken här kan innehålla två eller flera operationer. De grundläggande nyckelord som vi lär oss tidigare kommer att fungera som grund när vi arbetar med de mer utmanande matematiska fraserna att tolka till algebraiska uttryck.,
exempel 1: Skriv ett algebraiskt uttryck för matematikfrasen ”3 mer än två gånger ett tal”.
lösning: för att göra detta mycket lättare att förstå, kommer vi att dela upp denna fras i två delar. Först inser att vi har ett okänt nummer. Vi kan representera det med alla bokstäver i alfabetet. Låt det okända numret vara variabeln x. diagrammet nedan ska hjälpa oss att se vad som verkligen händer.,
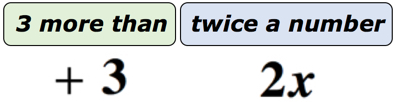
om du tänker på det finns det ett okänt nummer som representeras av variabel x som fördubblas eller multipliceras med 2. Vad är produkten, lägger vi till 3 till den. Så, vårt slutliga svar ska se ut som det nedan.
det slutliga svaret är 2x+3.
exempel 2: Skriv ett algebraiskt uttryck för matematikfrasen ”skillnaden på ett halvt tal och 10”.
lösning: Antag att variabeln y är det okända numret., Sökordet ”skillnad” uppmanar oss att vi ska utföra subtraktion. Det är viktigt här att vi uppmärksammar ordningen för subtraktion. Efter ordet ”skillnad” borde vi förvänta oss två kvantiteter. Den första kommer att vara minuend, medan den andra kommer att vara subtrahend. Ta en titt på diagrammet nedan.
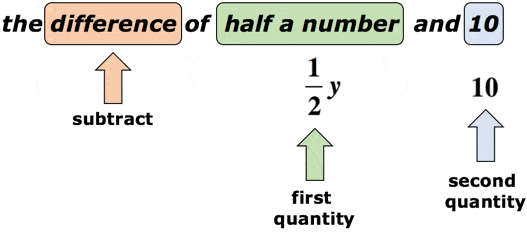
med hänvisning till diagrammet ovan kommer vi att subtrahera den första kvantiteten med den andra kvantiteten. Med andra ord subtraheras den andra kvantiteten från den första kvantiteten., Det slutliga svaret för matematikfrasen skulle vilja ha något så här,
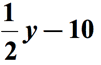
exempel 3: Skriv ett algebraiskt uttryck för matematikfrasen ”7 mindre än produkten av ett nummer och 6”.
lösning: vi vet att ”mindre än” föreslår en subtraktionsoperation. Men vi måste vara lite försiktiga här eftersom ordningen på hur vi subtraherar är viktig. Antag att det okända numret representeras av variabeln k. låt oss sätta detta på ett diagram för att få en känsla av det.,
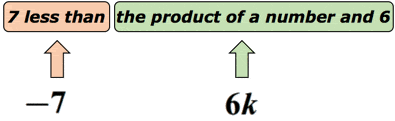
i själva verket kan denna matematiska fras skrivas om som
” produkten av ett nummer och 6 minus 7 ”
”7 mindre än” betyder ”minus 7” oavsett kvantitet som beskrivs som i det här fallet ”produkten av ett nummer och 6”. Här är den slutliga tolkningen av matematikfrasen i ett algebraiskt uttryck:
6k-7
exempel 4: Skriv ett algebraiskt uttryck för matematikfrasen ”genomsnittet av ett tal och 4”.,
lösning: för att komma igång med den här matematiska frasen måste vi granska vad ordet ”genomsnitt” betyder. För att beräkna genomsnittet eller medelvärdet av två eller flera siffror, vi kommer att behöva lägga upp alla nummer för att få en summa sedan dela den med antalet poster eller hur många siffror det finns. Om vi låter m vara variabeln för att representera det okända numret kan matematikfrasen ovan uttryckas i algebraiska uttryck som,
\ LARGE{{m + 4} \ over 2}
exempel 5: Skriv ett algebraiskt uttryck för matematikfrasen ”kvoten av 1 och 1 minskade med ett tal”.,
lösning: sökordet ”quotient” betyder att vi kommer att dela upp. I det här fallet vill vi dela numret 1 med kvantiteten 1 minskat med ett tal. Nedan är det algebraiska uttrycket som kan representera matematiska frasen ovan. Låt en vara det okända numret.
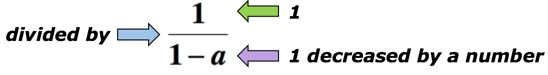
exempel 6: Skriv ett algebraiskt uttryck för matematikfrasen”en tredjedel av kvadraten på ett tal, ökat med 2″.
Lösning: Det pågår några saker här., För det första kan den del av frasen som anger ”en tredjedel av kvadraten av ett tal ”tolkas som” kvadraten av ett tal dividerat med 3 ”. Vi kommer att behöva höja det okända numret med 2 sedan dividera med 3. Antag att det okända numret är t, vi får
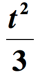
Vi är inte färdiga ännu. Det sista steget att göra är att lägga till kvantiteten ovan med 2 för att införliva den återstående delen av frasen ” ökat med 2 ”. Så här är den slutliga representationen av den givna matematiska frasen.,
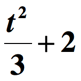
You might also be interested in:
Algebraic Expressions
Algebraic Sentences Word Problems