aproximare liniară
să spunem că într-o zi ai uitat un calculator și chiar vrei să afli cum este rădăcina pătrată a lui 2. Cum am afla fără un calculator? Putem folosi aproximarea liniară!Linearizarea unei funcții este doar despre găsirea liniei tangente a funcției într-un anumit punct într-un mod diferit., De liniarizare formula este:

unde L(x) este ecuația de linie tangentă la punctul a.
Ce este acest lucru util pentru noi? Ei bine, putem folosi de fapt această ecuație pentru a aproxima valorile funcției în apropierea punctului A. uitați-vă la acest grafic.,
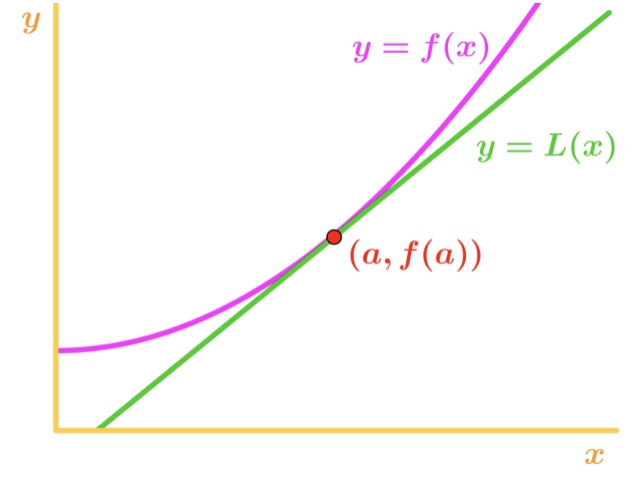
Observa că pentru valori x în apropiere de punctul o, vom vedea că funcția și linia tangentă este relativ aproape unul de altul. Din acest motiv, putem scrie că funcția este aproximativ egală cu linia tangentă din apropierea punctului a., Cu alte cuvinte,

în cazul în care ≈\cca≈ este de aproximativ simbol. Această ecuație este cunoscută sub numele de Formula de aproximare liniară. Este liniar într-un sens că tangenta este o linie dreaptă și o folosim pentru a aproxima funcția. Folosind această aproximare, putem aproxima valori care nu pot fi realizate manual. De exemplu, rădăcina pătrată a 2 sau jurnalul natural al 5 poate fi aproximată!, Un lucru important de reținut este că această aproximare funcționează numai pentru valorile x lângă punctul A. Dacă aveți o valoare x departe de punctul a, atunci aproximarea devine cu adevărat inexactă.
acum nu ne aruncăm o privire la câteva exemple de a găsi liniarizarea unei funcții și apoi uita-te la modul de utilizare aproximare liniară!
Găsi liniarizare a L(x) a funcției într-un
Întrebarea 1: se Consideră funcția
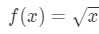
Să spunem că vrem să găsim liniarizare a funcției în punctul a=4.
Pentru a găsi liniarizare L(x), reamintim că,

- Pasul 1: Gaseste un
- Pasul 2: f(a)
- Pasul 3: Gaseste f'(a).
- Pasul 4: Conectați toate cele trei în formula pentru a găsi L(x)
-
să urmăm acești pași!,
Pasul 1: din fericire, a = 4 ne este dat în întrebare, deci nu trebuie să o căutăm.
- Pasul 2:
Observați că
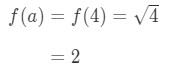
Ecuația 1: Liniarizare intrebare pt. 3 - Pasul 3:
Știu că derivat din rădăcini pătrate este
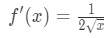
Ecuația 1: Liniarizare intrebare pt., 4 And so plugging in x=a gives us:
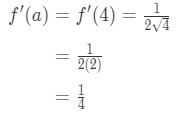
Equation 1: Linearization question pt. 5 - Step 4:
Since we know a, f(a), and f'(a), we can now plug it into L(x) to find the linearization of f(x).
Hence,
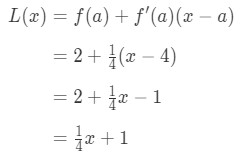
Equation 1: Linearization question pt., 6 Deci L(x)=14\frac{1}{4}41x+1 este liniarizare a acestei funcții în punctul x=4. În plus, este și linia tangentă a funcției la punctul x=4.
cum se face aproximarea liniară
amintiți-vă mai devreme am spus că putem folosi ecuația liniei tangente pentru a aproxima valorile funcției lângă a? Să încercăm acest lucru cu liniarizarea pe care am găsit-o mai devreme. Reamintim că,
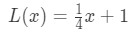
pentru punctele de lângă x=4. Putem schimba acest lucru într-un liniare de aproximare pentru f(x) prin a spune că:
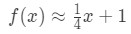
acum, să spunem că vreau să aproximez f(4.04). Dacă ar fi să conectați acest lucru la funcția originală, atunci veți obține 4.04\sqrt{4.04}4.04 . Acest lucru ar fi foarte greu de calculat fără un calculator., Cu toate acestea, folosind o aproximare liniară, putem spune că

Acum până în prezent, aceste întrebări ne-a dat o funcție și un punct de a lucra cu. Ce se întâmplă dacă nici unul dintre acestea au fost date la toate? Ce se întâmplă dacă întrebarea ne spune doar să estimăm un număr?
folosiți aproximarea liniară pentru a estima un număr
Să presupunem că dorim să estimăm 10 \ sqrt{10}10. Cum am face-o?, Ar trebui să folosim aproximarea liniară

dar nu avem nici măcar o funcție și un punct cu care să lucrăm. Aceasta înseamnă că trebuie să le facem noi înșine. Acest lucru ne conduce să facem următorii pași:
- Pasul 1: creați o funcție
- Pasul 2: creați-litera a
- Pasul 3: Gaseste f(a) și f'(a)
- Pasul 4: Conectați totul în formula de aproximare liniară
Să urmați pașii!,
întrebarea 2: estimarea 10\sqrt{10}10
- Pasul 1: să vină cu o funcție. Rețineți că suntem estimarea
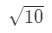
Ecuația 3: Estimare liniar cu aprox. pt.2 trebuie să facem cumva o relație între f(x) și 10\sqrt{10}10. Nu putem spune că f(x) = 10\sqrt{10}10 deoarece funcția nu va depinde de x. deci, de ce nu facem asta? Să
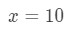
Ecuația 3: Estimare liniar cu aprox. pt.,3 Dacă facem asta, atunci suntem practic spune
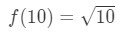
Ecuația 3: Estimare liniar cu aprox. pt.4 acum putem spune în mod evident care ar trebui să fie funcția. Să
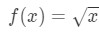
Ecuația 3: Estimare liniar cu aprox. pt.5 Deci avem o funcție, dar acum avem nevoie de un punct pentru a lucra cu.,
- pasul 2:
cheia pentru a găsi valoarea corectă a este luând în considerare două lucruri:
1) Asigurați-vă că valoarea a este aproape de x
2) Asigurați-vă că f(a) este un număr frumos.
ar fi a = 8 suficient? Ei bine, 8 este destul de aproape de 10, deci nu este rău. Cu toate acestea,
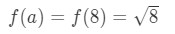
Ecuația 3: Estimare liniar cu aprox. pt.6 Observați că 8\sqrt{8}8 nu este un număr foarte frumos. De fapt, veți obține o grămadă de numere zecimale. Așa că trebuie să încercăm altceva.,
ar fi a = 9 suficient? Din nou, 9 este destul de aproape de 10, deci este în regulă. De asemenea,

Ecuația 3: Estimare liniar cu aprox. pt.7 f(a) este de fapt un frumos număr întreg aici, așa că acest lucru funcționează de fapt! Deci alegerea a = 9 este suficientă.
- Pasul 3:
Rețineți că de mai devreme:

Ecuația 3: Estimare liniar cu aprox. pt.,8 Calculating f'(x) we have again:

Equation 3: Estimate with linear approx. pt.9 So
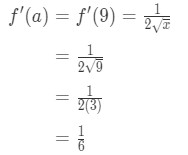
Equation 3: Estimate with linear approx. pt.,10 - Step 4:
Going back to the linear approximation formula we have:

Equation 3: Estimate with linear approx. pt.11 Plugging a, f(a), f'(a), f(x), and x in our formula you will see that:

Equation 3: Estimate with linear approx. pt.12 Hence, we just approximated the number!,dacă doriți mai multe probleme de practică cu privire la aproximarea liniară, atunci vă recomand să vă uitați la acest link aici.
http://tutorial.math.lamar.edu/Classes/CalcI/LinearApproximations.aspx
supraestimați și subestimați
știm că aproximarea liniară este doar o estimare a valorii funcției la un punct specificat. Cu toate acestea, de unde știm că dacă estimarea noastră este o supraestimare sau o subestimare? Calculăm al doilea derivat și privim concavitatea.,
Concave up vs Concave down
dacă a doua derivată a funcției este mai mare decât 0 pentru valorile apropiate de a, atunci funcția este concavă în sus. Acest lucru înseamnă că aproximarea noastră va fi o subestimare. Cu alte cuvinte,
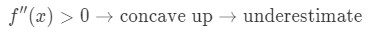
Formula 3: Subestima de Ce? Să aruncăm o privire la acest grafic.,
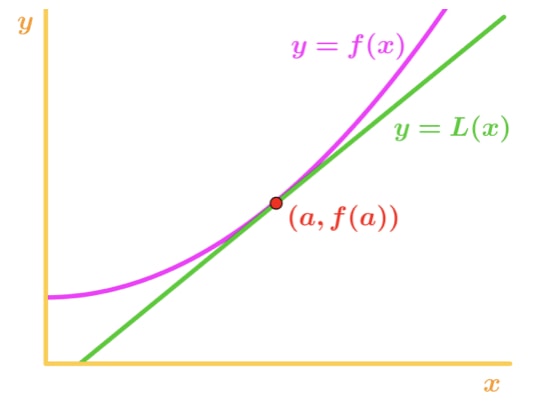
Grafic 2: Concavă în sus subestima Observați că f(x) este concavă în sus și linia tangentă este chiar sub f(x). Să presupunem că au fost de a utiliza linia tangenta pentru a aproxima f(x). Apoi, valorile Y ale liniei tangente vor fi întotdeauna mai mici decât valoarea reală a lui f(x). Prin urmare, avem o subestimare
acum, dacă al doilea derivat al funcției este mai mic decât 0 pentru valorile apropiate de a, atunci funcția este concavă în jos., Aceasta înseamnă că aproximarea noastră va fi o supraestimare. Cu alte cuvinte,
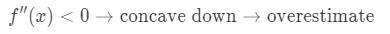
Formula 4: Supraestima din Nou, de ce? Să aruncăm o privire la un alt grafic.
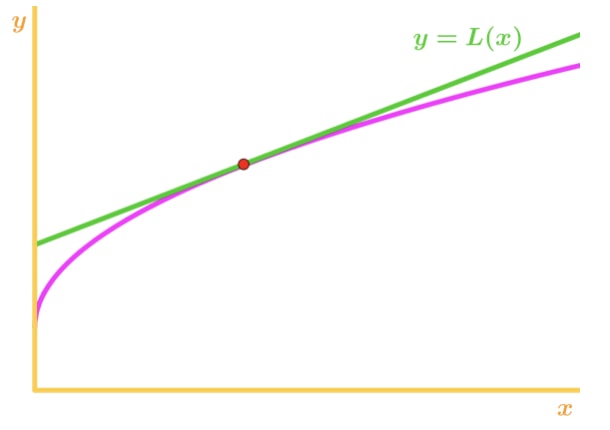
Grafic 3: Concavă în jos supraestima Observați că f(x) este concavă în jos și linia tangentă este chiar deasupra f(x). Din nou, să spunem că vom folosi linia tangentă pentru a aproxima f(x)., Apoi, valorile Y ale liniei tangente vor fi întotdeauna mai mari decât valoarea reală a lui f(x). Prin urmare, avem o supraestimare.
Deci, dacă aveți vreodată nevoie pentru a vedea dacă valoarea ta este o subestimare sau supraestimare, asigurați-vă că urmați acești pași:
- Pasul 1: Gaseste cea de-a doua derivate
- Pasul 2: uita-te la concavitate ale funcției lângă litera a
- Pas 3: Confirm că este o subestimare/supraestima
Să aruncăm o privire la un exemplu:
Întrebarea 3: f(x) = x\sqrt{x}x și a = 4. Dacă liniar aproximativ f (4.,04), ar fi o supraestimare sau o subestimare?
- Pasul 1: a se Vedea că
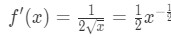
Ecuația 4: Supraestima intrebare pt.1 Deci a doua derivată este
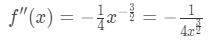
Ecuația 4: Supraestima intrebare pt.2 - Pasul 2:
Observați că a=4, deci vrem să se uite la valori pozitive ale lui x aproape 4. Acum uită-te la al doilea derivat., Când x este pozitiv, vom vedea că
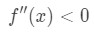
Ecuația 4: Supraestima intrebare pt.3 prin Urmare, este concavă în jos
- Pasul 3:
știm că, dacă funcția este concavă în jos, atunci tangenta linie va fi mai sus funcția. Prin urmare, utilizarea liniei tangente ca aproximare va da o valoare supraestimată.
diferențialele
nu numai că putem aproxima valorile cu aproximație liniară, dar putem aproxima și cu diferențialele., Pentru a aproxima, vom folosi următoarea formulă
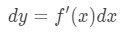
Formula 5: Diferentiale în cazul în care u și dx sunt diferențele, și f'(x) este derivata lui f în termeni de x. Deoarece avem de-a face cu foarte mici modificări în x și y, atunci vom folosi faptul că:
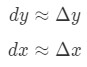
Ecuația 5: Aproximarea diferențele pt.,1 cu toate Acestea, cele mai multe dintre întrebările la care nu implica setarea
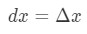
Ecuația 5: Aproximarea diferențele pt.2 folosind aceste fapte ne va conduce să aibă:
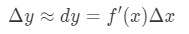
Ecuația 5: Aproximarea diferențele pt.3 Această aproximare este foarte util atunci când aproximarea schimbare de y., Rețineți că atunci nu aveau calculatoare, deci aceasta este cea mai bună aproximare pe care o puteau obține pentru funcții cu rădăcini pătrate sau bușteni naturali.de cele mai multe ori va trebui să căutați singur f'(x) și Δ\DeltaΔx. Cu alte cuvinte, urmați acești pași pentru a aproxima Δ \ DeltaΔy!
- Pasul 1: Găsiți Δ \ DeltaΔx
- Pasul 2: Găsiți f ‘ (x)
- Pasul 3: Conectați totul în formula pentru a găsi dy. dy va fi aproximarea pentru Δ \ DeltaΔy.
să ne uităm la un exemplu de utilizare a acestei aproximări:
întrebarea 4: luați în considerare funcția y = ln(x + 1)., Să presupunem că X se schimbă de la 0 la 0.01. Aproximativ Δ \ DeltaΔy.
- Pasul 1: se Observa ca x se modifică de la 0 la 0.01, deci, o schimbare în x ar fi:
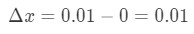
Ecuația 6: Diferențial intrebare pt.1 - Pasul 2:
derivat ar fi:
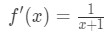
Ecuația 6: Diferențial intrebare pt.,2 - Pasul 3:
Conectarea totul în am:
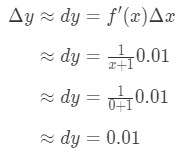
Ecuația 6: Diferențial intrebare pt.3 prin Urmare, Δ\DeltaΔy ≈\cca≈ 0.01
cu toate Acestea, cele mai multe ori ne dorim să estimăm o valoare a funcției, și nu de schimbare a valorii. Prin urmare, vom adăuga din ambele părți ale ecuației de y, care ne dă:
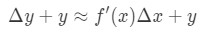
Ecuația 6: Diferențial intrebare pt.,4 care este aceeași ca:
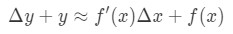
Ecuația 6: Diferențial intrebare pt.5 această ecuație este puțin greu de citit, așa că o vom rearanja și mai mult. Să încercăm să scăpăm de Y și Δ \ DeltaΔy. Observați că Δ\DeltaΔy+ y este în esență același ca și găsirea valoarea funcției la Δ\DeltaΔx+x. Cu alte cuvinte,
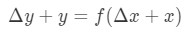
Ecuația 6: Diferențial intrebare pt.,6 prin Urmare, înlocuind aceasta în apropiere noastre de mai sus ne va da:
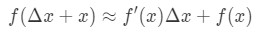
Ecuația 6: Diferențial intrebare pt.7 în cazul în care f(Δ\DeltaΔx+x) este valoarea pe care încercăm să o estimeze. Cum folosim această formulă? Vă recomandăm să urmați acești pași:
să folosim acești pași pentru următoarea întrebare.
Întrebarea 5: folosiți diferențialele pentru a aproxima 10\sqrt{10}10.
- Pasul 1: comparați f (Δ\DeltaΔx + x) cu 10 \ sqrt{10}10., Since 10\sqrt{10}10 has a square root and 9 is a perfect square that is closest to 10, then let
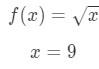
Equation 7: Approximate value with differentials pt.1 Notice that:
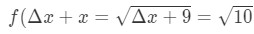
Equation 7: Approximate value with differentials pt.,2 Vedea că nu există nici o alegere, ci să Δ\DeltaΔx = 1
- Pasul 2:
a se Vedea că derivat dă:

Ecuația 7: valoare Aproximativă cu diferențele pt.3 Deci, acest lucru implică
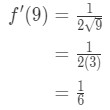
Ecuația 7: valoare Aproximativă cu diferențele pt.,4 - Pasul 3:
Conectarea totul în formulă ne dă:
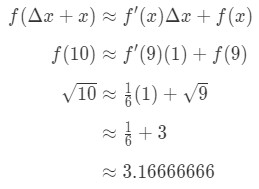
Ecuația 7: valoare Aproximativă cu diferențele pt.5 prin urmare, am aproximat doar numărul.un lucru interesant de observat este că aproximarea liniară și diferențialele dau același rezultat pentru 10\sqrt{10}10.,
Dacă doriți să aflați mai multe despre diferențele, faceți clic pe acest link:
http://tutorial.math.lamar.edu/Classes/CalcI/LinearApproximations.aspx
Dovedindu-Am’Hospital e Regula folosind aproximare liniară
Acum am învățat o mulțime de lucruri despre aproximare liniară, dar ce altceva putem face cu ea? Putem folosi de fapt formula de aproximare liniară pentru a dovedi o regulă cunoscută sub numele de regula l ‘ Hospital lui . Iată cum funcționează dovada.
Amintiți-vă că liniare formula de aproximare este:

Ecuația 8: Derivă l ‘ hopital e regula pt.,1 a se Vedea că putem rearanja formula astfel încât:
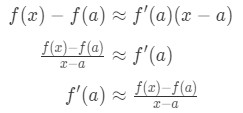
Ecuația 8: Derivă l ‘ hopital e regula pt.2 dai Seama că aproximare devine mai mult și mai precis ca vom alege x valorile care sunt mai aproape de un. Cu alte cuvinte, dacă vom lua limita când x→a, atunci ei vor egale. Deci,
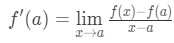
Ecuația 8: Derivă l ‘ hopital e regula pt.,3 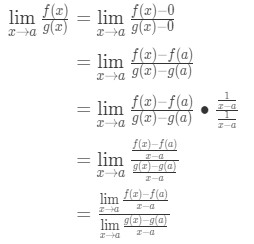
Ecuația 8: Derivă l ‘ hopital e regula pt.4 Acum, observați că putem aplica formula de la care am derivat mai devreme aici. Deci, acum,
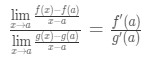
Ecuația 8: Derivă l ‘ hopital e regula pt.5 Acum, în loc de a scrie f'(o) și g'(o), putem aplica limite ca x→a (pentru că știm că f și g sunt derivabile)., Deci,
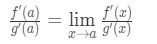
Ecuația 8: Derivă l ‘ hopital e regula pt.6 prin Urmare, am arătat că:
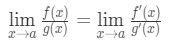
Formula 6: Regula lui L ‘ hopital care este L’Hospital e Regula .
când să folosim regula l ‘hopital
întotdeauna dorim să aplicăm regula l’ optial atunci când întâlnim limite nedeterminate. Există două tipuri de forme nedeterminate., Aceste nedeterminată forme ar fi:
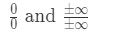
Formula 7: Nedeterminată forme O mulțime de oameni fac greseala de a folosi regula lui l ‘ hopital, fără să verifice dacă este o perioadă nedeterminată de limită. Deci, asigurați-vă că îl verificați mai întâi! În caz contrar, nu va funcționa și veți primi un răspuns greșit. Iată un ghid pentru utilizarea regulii l ‘ hopital:
- Pasul 1: Evaluați limita direct.
- Pasul 2: Verificați dacă este una dintre formele nedeterminate. Dacă este, mergeți la Pasul 3.,
- Pasul 3: utilizați regula l ‘ hopital lui.
- Pasul 4: Verificați dacă primiți un alt formular nedeterminat. Repetați Pasul 3 dacă faceți acest lucru.
Să aruncăm o privire la câteva exemple folosind acești pași.
Întrebarea 6: Evaluarea limita
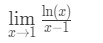
Ecuația 9: regula lui L ‘ hopital intrebare pt.1 - Pasul 1: Evaluarea limită direct ne dă
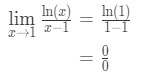
Ecuația 9: regula lui L ‘ hopital intrebare pt.,2 - Pasul 2:
Da, este una dintre cele nedeterminată forme.
- Pasul 3:
Aplică regula lui l ‘ hopital avem:
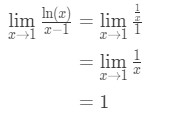
Ecuația 9: regula lui L ‘ hopital intrebare pt.3 - Pasul 4:
nu este o formă nedeterminată, așa că am sunt de făcut, iar răspunsul este 1.
acum, această întrebare a fost un pic mai ușor, așa că de ce nu aruncăm o privire la ceva care este un pic mai greu.,
Întrebarea 7: Evaluarea limita
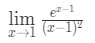
Ecuația 10: regula lui L ‘ hopital de două ori intrebare pt.1 - Pasul 1: Evaluarea limită direct, vom vedea că:
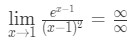
Ecuația 10: regula lui L ‘ hopital de două ori intrebare pt.2 - pasul 2:
aceasta este o formă nedeterminată, deci mergeți la Pasul 3.,
- Pasul 3:
Aplică regula lui l ‘ hopital avem
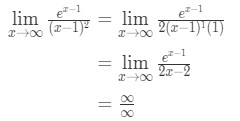
Ecuația 10: regula lui L ‘ hopital de două ori intrebare pt.3 - Pasul 4:
Aceasta este o altă formă nedeterminată. Așa că trebuie să ne întoarcem la Pasul 3 și să aplicăm din nou regulile lui l ‘ optial.
- Pasul 3:
Aplică regula lui l ‘ hopital din nou, avem:
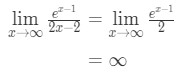
Ecuația 10: regula lui L ‘ hopital de două ori intrebare pt.,4 - Pasul 4:
Infinit nu este o formă nedeterminată, așa că am sunt de făcut, iar răspunsul este ∞\infty∞