suponha que deseja considerar o impacto de um factor de risco no tempo até à ocorrência de um evento. Por exemplo, Arnlov et al (2010) consideram o impacto do Índice de Massa Corporal (IMC) e da síndrome metabólica no desenvolvimento de doenças cardiovasculares e morte em homens de meia-idade. As associações foram investigadas utilizando dados de um estudo de coorte de 1758 homens suecos de meia-idade residentes num condado com mais de 30 anos de acompanhamento., A figura abaixo mostra o tempo para um evento cardiovascular importante por categoria de IMC e presença (b) ou ausência (a) de síndrome metabólica. Há alguma diferença nestas curvas de sobrevivência?
Figura 2: curvas Kaplan-Meier Para grandes eventos cardiovasculares em diferentes categorias de IMC em indivíduos sem MetS (a) e com MetS (B).
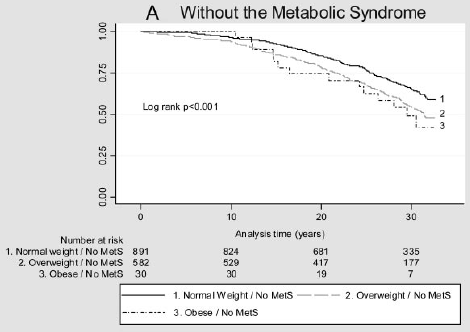
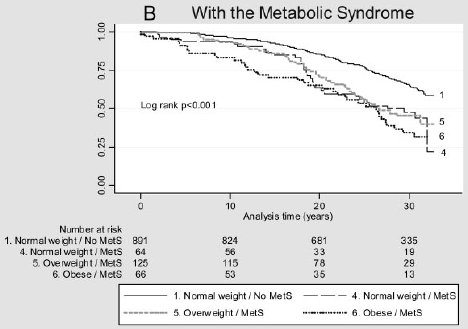
(Figuras reproduzidas a partir de Arnlov, J et al., Impacto do Índice de Massa Corporal e da síndrome metabólica no risco de doença Cardiovascular e morte em homens de meia-idade. Circulation 2010; 121; 230-236, originally published online 12/28/2009; DOI 10.1161/CIRCULATIONAHA.109, 88752)
a ocorrência de um evento cardiovascular principal é uma resposta binária. A regressão logística, com BMI como variável predictor, seria apropriada para analisar esses dados?,
resposta
a relação entre a presença ou ausência de um evento cardiovascular principal e a variável predictor pode ser avaliada com regressão logística em um determinado momento, mas isso não compararia diretamente as curvas de sobrevivência. Uma análise de sobrevivência compararia as curvas com base no tempo com o evento.os métodos de Análise de sobrevivência, tais como a regressão proporcional dos perigos, diferem da regressão logística avaliando uma taxa em vez de uma proporção.,
regressão logística em contraste, considera a proporção de novos casos que se desenvolvem num determinado período de tempo, ou seja, a incidência cumulativa., A regressão logística estima a razão de probabilidade; a regressão proporcional dos perigos estima a razão de perigo.
a razão das funções de perigo pode ser considerada uma razão das funções de risco, de modo que o modelo proporcional de regressão de Riscos pode ser considerado como função do risco relativo (enquanto os modelos de regressão logística são uma função de uma razão de probabilidades). As alterações num covariato têm um efeito multiplicativo no risco basal. O modelo em termos da função de perigo no momento t é:
\(\lambda \left (t / X_{1i}, X_{2i},…,X_{Ki} \right )=\lambda_{0} (t)exp\left ( \beta_{1}X_{1i}+\beta_{2}X_{2i}+…,+\beta_{K}X_{Ki} \right)\)
embora nenhum modelo de probabilidade particular seja selecionado para representar os tempos de sobrevivência, a regressão proporcional dos perigos tem uma suposição importante: o perigo para qualquer indivíduo é uma proporção fixa do perigo para qualquer outro indivíduo. (isto é, perigos proporcionais)., Aviso se \(\lambda_0 (t)\) é a função de risco para um assunto com todos os valores de prognósticos igual a zero e \(\lambda_1 (t)\) é a função de risco para um assunto com outros valores para as variáveis preditoras, em seguida, o hazard ratio depende apenas as variáveis preditoras e não no tempo t. Este pressuposto significa que, se uma covariável duplica o risco de o evento no primeiro dia, ele também dobra o risco do evento em qualquer outro dia.,
modelos de perigos proporcionais podem ser usados para medidas discretas ou contínuas de tempo de Evento e podem incorporar covariados dependentes do tempo (covariantes cujos valores podem mudar durante o período de observação). Utilizando a regressão proporcional dos perigos, podem ser produzidas razões de risco (ou risco) ajustadas pela covariação.vamos voltar à questão original colocada por Arnlov e Arnlov. colleagues…do o IMC e a síndrome metabólica afectam o desenvolvimento de doenças cardiovasculares? Leia o Arnlov et al., Impacto do Índice de Massa Corporal e da síndrome metabólica no risco de doença Cardiovascular e morte em homens de meia idade circulação 2010;121;230-236, dando especial atenção aos métodos estatísticos, resultados e conclusões.
comparar e contrastar a abordagem proporcional de regressão de riscos a uma abordagem de regressão logística por leitura Franco et al. Trajectories of Entering the Metabolic Syndrome: The Framingham Heart Study. Circulation 2009; 120; 1943-1950; originally published online Nov 2, 2009; American Heart Association. 7272 Greenville Avenue, Dallas, TX DOI: 10.,1161 / CIRCULATIONAHA.109, 855817
Pode também comparar os resultados dos dois estudos. Ambos os papéis estão na pasta de leitura da 14ª semana.Nota! Se você não está familiarizado com curvas Kaplan-Meier, leia o capítulo de Análise de sobrevivência no Research Methods II monographs do Journal of Tropical Pediatrics
(acessado a partir de http://www.oxfordjournals.org/our_journals/tropej/online/ma_chap12.pdf )