After the radius and diameter, another important part of a circle is an arc. Neste artigo, discutiremos em detalhes o que é um arco, como encontrar o comprimento de um arco e a medição de um comprimento de arco em radianos. Estudaremos também o arco menor e o arco maior.o que é um arco de um círculo?um arco de um círculo é qualquer porção da circunferência de um círculo. Para recordar, a circunferência de um círculo é o perímetro ou a distância em torno de um círculo., Portanto, podemos dizer que a circunferência de um círculo é o arco completo do próprio círculo.
como encontrar o comprimento de um arco?
a fórmula para calcular O arco afirma que:
comprimento de Arco = 2nr (θ/360)
Onde, r = raio do círculo,
π = pi = 3.14
θ = ângulo (em graus) subtendido por um arco no centro do círculo.
360 = o ângulo de uma rotação completa.
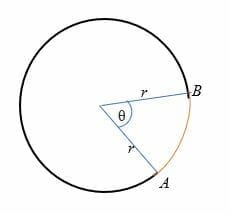
da ilustração acima, o comprimento do arco (desenhado a vermelho) é a distância do ponto A ao ponto B.,
Let’s work out a few example problems about the length of an arc:
Example 1
Given that arc AB subtends an angle of 40 graus to the center of a circle whose radius is 7 cm. Calcular o comprimento de arc AB.
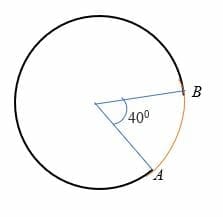
Solução
Dado r = 7 cm
θ = 40 graus.
Por substituição,
O comprimento de um arco = 2nr(θ/360)
Comprimento = 2 x 3.14 x 7 x 40/360
= 4.884 cm.
Exemplo 2
encontra o comprimento de um arco de um círculo que subtende um ângulo de 120 graus ao centro de um círculo cujo raio é de 24 cm.,
Solução
O comprimento de um arco = 2nr(θ/360)
= 2 x 3.14 x 24 x 120/360
= 50.24 cm.
exemplo 3
O comprimento de um arco é de 35 m. Se o raio do círculo for de 14 m, encontre o ângulo pretendido pelo arco.
Solução
O comprimento de um arco = 2nr(θ/360)
35 m = 2 x 3.14 x 14 x (θ/360)
35 = 87.92 θ/360
Multiplique ambos os lados por 360 para remover a fração.
12600 = 87.92 θ
Divide ambos os lados por 87.92
θ = 143.3 graus.,
exemplo 4
encontre o raio de um arco com 156 cm de comprimento e subtenda um ângulo de 150 graus ao centro de um círculo.
Solução
O comprimento de um arco = 2nr(θ/360)
156 cm = 2 x 3.14 x r x 150/360
156 = 2.6167 r
Dividir ambos os lados por 2.6167
r = 59.62 cm.o raio do arco é de 59,62 cm.
como encontrar o comprimento do Arco EM radianos?
existe uma relação entre o ângulo pretendido por um arco em radianos e a relação entre o comprimento do arco e o raio do círculo., Neste caso,
θ = (o comprimento de um arco) / (o raio do círculo).
Portanto, o comprimento do arco em radianos é dada por,
S = r θ
onde, θ = ângulo subtendido por um arco em radianos
S = comprimento do arco.
r = raio do círculo.
um radiano é o ângulo central pretendido por um comprimento de arco de um raio, ou seja, s = r
o radiano é apenas outra forma de medir o tamanho de um ângulo. Por exemplo, para converter ângulos de graus para radianos, multiplique o ângulo (em graus) Por π/180.,
da mesma forma, para converter radianos em graus, multiplique o ângulo (em radianos) por 180/π
Exemplo 5
a Encontrar o comprimento de um arco cujo raio é de 10 cm e o ângulo subtendido é 0.349 radianos.
solução
Comprimento Do Arco = r θ
= 0, 349 x 10
= 3, 49 cm.
exemplo 6
encontrar o comprimento de um arco em radianos, que tem um raio de 10 m e um ângulo de 2.356 radianos.
Solução
comprimento de Arco = r θ
= 10 m x 2.356
= 23.56 m.
Exemplo 7
a Encontrar o ângulo subtendido por um arco que tem um comprimento de 10.05 mm e um raio de 8 mm.,
Solução
comprimento de Arco = r θ
10.05 = 8 θ
Dividir ambos os lados por 8.
1.2567 = θ
lá, o ângulo pretendido pelo arco é 1.2567 radianos.
exemplo 8
calcular o raio de um círculo cujo comprimento de arco é de 144 jardas e ângulo de arco, é de 3,665 radianos.
Solução
comprimento de Arco = r θ
144 = 3.665 r
Dividir ambos os lados por 3.665.
144/3.665 = r
r = 39.29 jardas.
exemplo 9
Calcule o comprimento de um arco que subtende um ângulo de 6.283 radianos ao centro de um círculo com um raio de 28 cm.,
Solução
comprimento de Arco = r θ
= 28 x 6.283
= 175.93 cm
Menor arco (h3)
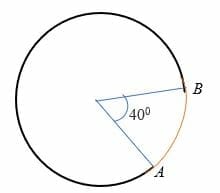
O menor arco é um arco que subtende um ângulo de menos de 180 graus para o centro do círculo. Em outras palavras, o arco menor mede menos de um semicírculo e é representado no círculo por dois pontos. Por exemplo, arco AB no círculo abaixo é o arco menor.
arco maior (h3)
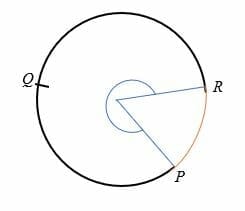
o arco maior de um círculo é um arco que subtende um ângulo de mais de 180 graus ao centro do círculo., O arco maior é maior que o semicírculo e é representado por três pontos em um círculo.
Por exemplo, PQR é o arco principal do círculo mostrado abaixo.
a Prática de Problemas
- Encontrar a área do setor do círculo de raio de 9 mm. Suponha que o ângulo subtendido por este arco, o centro é de 30 o.
- Cidade é devido a Norte da cidade B. As latitudes da cidade A e a cidade B são 54 o N e 45 s de N, respectivamente. Qual é a distância Norte-Sul entre as duas cidades? O raio da Terra é de 6400 km.,