nie ma jednej strategii tłumaczenia fraz matematycznych na Wyrażenia algebraiczne. Dopóki pamiętasz podstawy, powinieneś być w stanie poradzić sobie z trudniejszymi. Po prostu upewnij się, że możesz uzasadnić, w jaki sposób wymyślasz własne wyrażenie algebraiczne, a co ważniejsze, że ma to dla ciebie sens. Zawsze poproś nauczycieli o pomoc lub współpracuj z kolegami z klasy, aby zweryfikować swoje odpowiedzi.,
aby rozwinąć swoje umiejętności w pisaniu wyrażeń algebraicznych, omówimy różne sposoby, w jaki każda operacja może pojawić się jako słowo lub fraza w problemie. Cztery operacje arytmetyczne to dodawanie, odejmowanie, mnożenie i dzielenie.,
Key Words for Addition

Key Words for Subtraction

Key Words for Multiplication

Key Words for Division

It is time now time to go over some examples to practice writing algebraic expressions., Dzielę przykłady na dwa:
- podstawowe przykłady wyrażeń algebraicznych
- wieloczęściowe przykłady wyrażeń algebraicznych
podstawowe wyrażenia algebraiczne przykłady
przykład 1: Napisz wyrażenie algebraiczne dla wyrażenia matematycznego „suma liczby i czterech”.
rozwiązanie: słowo „suma” od razu daje nam wskazówkę, którą zamierzamy tutaj dodać. Zauważ, że chcemy dodać dwie ilości: jedną nieznaną liczbę i liczbę 4. Ponieważ nie wiemy jaka jest wartość liczby, możemy użyć zmiennej do jej reprezentowania., Możesz używać dowolnych liter alfabetu. W tym przypadku, zgodzimy się użyć y dla zmiennej.
gdy dodamy zmienną y i 4, mamy y + 4. Można też napisać odpowiedź jako 4 + y, ponieważ dodawanie jest przemienne – czyli zmiana kolejności dodawania nie zmienia jej sumy.
ostateczna odpowiedź to y+4.
przykład 2: Napisz wyrażenie algebraiczne dla wyrażenia matematycznego „10 powiększone o liczbę”.
rozwiązanie: słowa kluczowe „increased by” oznaczają dodanie. Oznacza to, że nieznana liczba została dodana do 10., Używając litery k jako zmiennej, możemy przetłumaczyć powyższe wyrażenie jako 10 + K. ponieważ dodawanie jest przemienne, możemy przepisać je jako k + 10. Jedna z dwóch powyższych odpowiedzi jest poprawna.
ostateczna odpowiedź to k+10.
przykład 3: Napisz wyrażenie algebraiczne dla wyrażenia matematycznego „różnica 1 i liczba”.
rozwiązanie: słowo „różnica” sugeruje, że zamierzamy odjąć. Ponadto, gdy napotkasz to słowo matematyczne (różnica) upewnij się, że zwracasz uwagę na kolejność. Pierwsza jest liczba 1, a druga nieznana liczba., Oznacza to, że liczba 1 to minuend, a nieznana liczba to subtrahend. Jeśli zdecydujemy się użyć litery x jako naszej zmiennej, odpowiedź staje się 1-x.
ostateczna odpowiedź to 1 – x.
przykład 4: napisz wyrażenie algebraiczne dla wyrażenia matematycznego „liczba mniejsza niż 8”.
rozwiązanie: bądź bardzo ostrożny, gdy masz do czynienia ze słowami kluczowymi „mniej niż”. Pierwsza ilość, która pojawia się przed słowami kluczowymi „mniej niż”, która jest „liczbą”, jest podzbiorem. Podczas gdy ilość, która przychodzi po nim, staje się drobiazgiem.,
innymi słowy, odejmujemy nieznaną liczbę od liczby 8. Jeśli wybierzemy naszą zmienną na literę a, otrzymamy 8-a.
ostateczna odpowiedź to 8 – a.
przykład 5: napisz wyrażenie algebraiczne dla wyrażenia matematycznego „iloczyn 5 i liczby”.
rozwiązanie: aby znaleźć iloczyn dwóch ilości lub wartości, oznacza to, że będziemy je mnożyć razem. Wybierając literę m jako naszą zmienną, wyrażenie algebraiczne dla tego wyrażenia matematycznego wynosi po prostu 5m. oznacza to 5 razy nieznaną liczbę m.
ostateczna odpowiedź to 5m.,
przykład 6: napisz wyrażenie algebraiczne dla wyrażenia matematycznego „dwa razy liczba”.
rozwiązanie: słowo „dwa razy” oznacza, że coś podwoimy. W tym przypadku chcemy podwoić nieznaną wartość lub ilość. Niech litera d będzie liczbą nieznaną, gdy ją podwoimy, otrzymamy wyrażenie algebraiczne 2d.
ostateczna odpowiedź to 2d.
przykład 7: napisz wyrażenie algebraiczne dla wyrażenia matematycznego „iloraz liczby i 7”.
rozwiązanie: słowo kluczowe „iloraz” oznacza, że wykonujemy operację dzielenia. Podzielimy nieznaną liczbę przez 7., Wybierając literę w jako naszą zmienną, powyższe wyrażenie matematyczne można wyrazić jako wyrażenie algebraiczne poniżej.
\LARGE{W \over 7}
przykład 8: napisz wyrażenie algebraiczne dla wyrażenia matematycznego „stosunek 10 i liczby”.
rozwiązanie: podobnie słowo „ratio” oznacza podział. Porządek tutaj jest bardzo ważny. Pierwsza Ilość to liczba 10, a druga Ilość to nieznana liczba. Oznacza to, że 10 jest dzielone przez nieznaną liczbę., Niech c będzie liczbą nieznaną, wyrażenie algebraiczne dla powyższej frazy matematycznej można zapisać jako
\LARGE{10 \over c}
wieloczęściowe Wyrażenia algebraiczne przykłady
tym razem zajmiemy się zwrotami matematycznymi, które są nieco bardziej złożone. Wyrażenia algebraiczne mogą zawierać dwie lub więcej operacji. Podstawowe słowa kluczowe, których uczymy się wcześniej, będą służyć jako podstawa podczas pracy z trudniejszymi zwrotami matematycznymi do interpretacji w Wyrażenia algebraiczne.,
przykład 1: Napisz wyrażenie algebraiczne dla wyrażenia matematycznego „3 więcej niż dwa razy liczba”.
rozwiązanie: aby było to znacznie łatwiejsze do zrozumienia, podzielimy to zdanie na dwie części. Po pierwsze, rozpoznaj, że mamy nieznany numer. Możemy ją reprezentować za pomocą dowolnych liter alfabetu. Niech nieznana liczba będzie zmienną x. poniższy diagram powinien pomóc nam zobaczyć, co naprawdę się dzieje.,
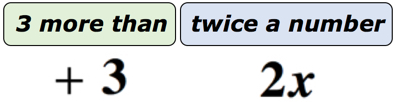
Jeśli myślisz o tym, istnieje nieznana liczba reprezentowana przez zmienną x, która jest podwojona lub pomnożona przez 2. Niezależnie od produktu, dodamy do niego 3. Tak więc nasza ostateczna odpowiedź powinna wyglądać jak ta poniżej.
ostateczna odpowiedź to 2x+3.
przykład 2: Napisz wyrażenie algebraiczne dla wyrażenia matematycznego „różnica połowy liczby i 10”.
rozwiązanie: Załóżmy, że zmienna y jest liczbą nieznaną., Słowo kluczowe „różnica” podpowiada nam, że mamy zamiar wykonać odejmowanie. Ważne jest tutaj, aby zwrócić uwagę na kolejność odejmowania. Po słowie „różnica” powinniśmy spodziewać się dwóch ilości. Pierwszy będzie minuendem, podczas gdy drugi będzie subtrahendem. Spójrz na poniższy diagram.
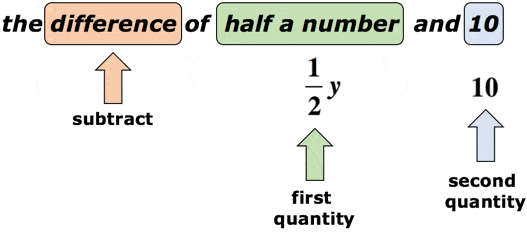
odwołując się do powyższego diagramu, odejmujemy pierwszą Ilość przez drugą ilość. Innymi słowy, druga ilość jest odejmowana od pierwszej ilości., Ostateczna odpowiedź dla wyrażenia matematycznego powinna wyglądać tak:
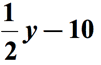
przykład 3: Napisz wyrażenie algebraiczne dla wyrażenia matematycznego „7 mniej niż iloczyn liczby i 6”.
rozwiązanie: wiemy, że „mniej niż” sugeruje operację odejmowania. Ale musimy być trochę ostrożni, ponieważ kolejność odejmowania jest ważna. Załóżmy, że nieznana liczba jest reprezentowana przez zmienną K. umieśćmy to na diagramie, aby to zrozumieć.,
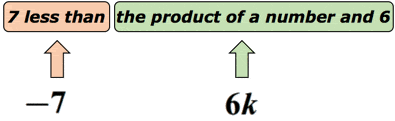
w rzeczywistości to zdanie matematyczne można przepisać jako
” iloczyn liczby i 6 minus 7 „
„7 mniej niż” oznacza „minus 7” do dowolnej ilości opisanej, która w tym przypadku „iloczyn liczby i 6”. Oto ostateczna interpretacja wyrażenia matematycznego w wyrażeniu algebraicznym:
6k-7
przykład 4: napisz wyrażenie algebraiczne dla wyrażenia matematycznego „średnia Liczby i 4”.,
rozwiązanie: aby rozpocząć pracę nad tą konkretną frazą matematyczną, musimy sprawdzić, co oznacza słowo „średnia”. Aby obliczyć średnią lub średnią z dwóch lub więcej liczb, będziemy musieli zsumować wszystkie liczby, aby uzyskać sumę, a następnie podzielić ją przez liczbę wpisów lub liczbę liczb. Jeśli M będzie zmienną reprezentującą nieznaną liczbę, powyższe wyrażenie matematyczne może być wyrażone w wyrażeniach algebraicznych jako,
\LARGE{{m + 4} \over 2}
przykład 5: napisz wyrażenie algebraiczne dla wyrażenia matematycznego „iloraz 1 i 1 zmniejszony o liczbę”.,
rozwiązanie: słowo kluczowe „iloraz” oznacza, że podzielimy. W tym przypadku chcemy podzielić liczbę 1 przez Ilość 1 pomniejszoną o liczbę. Poniżej znajduje się wyrażenie algebraiczne, które może reprezentować powyższe wyrażenie matematyczne. Niech a będzie nieznaną liczbą.
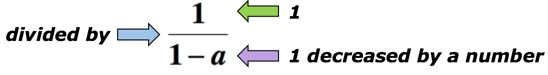
przykład 6: zapis wyrażenia algebraicznego dla wyrażenia matematycznego „jedna trzecia kwadratu liczby powiększona o 2”.
rozwiązanie: dzieje się tu kilka rzeczy., Po pierwsze, część zdania, która mówi „jedna trzecia kwadratu liczby”, może być interpretowana jako „kwadrat liczby podzielonej przez 3”. Będziemy musieli podnieść nieznaną liczbę przez 2, a następnie podzielić przez 3. Załóżmy, że nieznana liczba to t, otrzymujemy
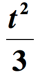
jeszcze nie skończyliśmy. Ostatnim krokiem do zrobienia jest dodanie powyższej ilości przez 2, aby włączyć pozostałą część wyrażenia „zwiększona o 2”. Oto ostateczna reprezentacja danej frazy matematycznej.,
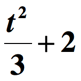
You might also be interested in:
Algebraic Expressions
Algebraic Sentences Word Problems