stel dat u de impact van een risicofactor op de tijd tot het optreden van een gebeurtenis wilt overwegen. Bijvoorbeeld, Arnlov et al (2010) overwegen de impact van body mass index (BMI) en metabool syndroom op de ontwikkeling van hart-en vaatziekten en overlijden bij mannen van middelbare leeftijd. De verenigingen werden onderzocht aan de hand van gegevens uit een cohortstudie van 1758 Zweedse mannen van middelbare leeftijd die in één provincie woonden en meer dan 30 jaar follow-up hadden., Onderstaande figuur toont de tijd tot een belangrijke cardiovasculaire gebeurtenis per BMI-categorie en aanwezigheid (B) of afwezigheid (a) van metabool syndroom. Is er een verschil in deze overlevingscurven?
Figuur 2: Kaplan-Meier-curves voor belangrijke cardiovasculaire voorvallen in verschillende BMI-categorieën bij individuen zonder MetS (A) en met MetS (B).
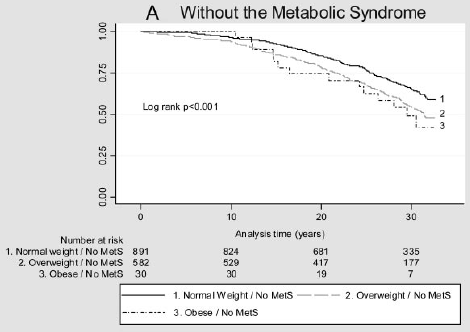
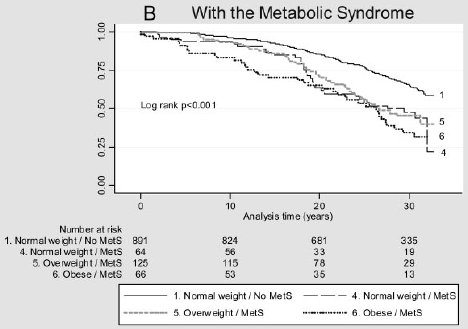
(cijfers van Arnlov, J et al., Impact van Body Mass Index en het metabool syndroom op het risico van hart-en vaatziekten en overlijden bij mannen van middelbare leeftijd. Oplage 2010; 121; 230-236, oorspronkelijk online gepubliceerd 28/12/2009; DOI 10.1161 / CIRCULATIONAHA.109.88752)
het optreden van een belangrijke cardiovasculaire gebeurtenis is een binaire respons. Zou logistische regressie, met BMI als voorspellende variabele, geschikt zijn om deze gegevens te analyseren?,
antwoord
de relatie tussen de aanwezigheid of afwezigheid van een belangrijke cardiovasculaire gebeurtenis en de voorspellende variabele kan op een bepaald moment worden bepaald met logistische regressie, maar dit zou de overlevingscurves niet direct met elkaar vergelijken. Een overlevingsanalyse zou de curves vergelijken op basis van de tijd met de gebeurtenis.
Overlevingsanalysemethoden, zoals regressie van proportionele risico ‘ s, verschillen van logistische regressie door een percentage te bepalen in plaats van een verhouding.,
logistische regressie in tegenstelling tot het aantal nieuwe gevallen dat zich in een bepaalde periode ontwikkelt, d.w.z. de cumulatieve incidentie., Logistic regression schat de odds ratio; proportional hazards regression schat de hazard ratio.
de verhouding van gevarenfuncties kan worden beschouwd als een verhouding van risicofuncties, zodat het proportionele risico-regressiemodel kan worden beschouwd als functie van het relatieve risico (terwijl logistische regressiemodellen een functie zijn van een odds ratio). Veranderingen in een covariabele hebben een multiplicatief effect op het basisrisico. Het model in termen van de gevarenfunctie op tijdstip t is:
\(\lambda \ left ( t / X_{1i}, X_{2i},…, X_{Ki} \right )=\lambda_{0} (t)exp\left (\beta_{1}X_{1i}+\beta_{2}X_{2i}+…,+ \beta_{K}X_{Ki} \right)\)
hoewel geen bepaald waarschijnlijkheidsmodel is geselecteerd om de overlevingstijden weer te geven, heeft regressie van proportionele gevaren een belangrijke aanname: het gevaar voor een individu is een vast deel van het gevaar voor een ander individu. (d.w.z. proportionele gevaren)., Merken als \(\lambda_0 (t)\) de hazard-functie voor een onderwerp met de voorspelde waarden gelijk aan nul en \(\lambda_1 (t)\) de hazard-functie voor een onderwerp met andere waarden voor de predictor variabelen, dan is de hazard ratio is slechts afhankelijk van de predictor variabelen en niet op tijd t. Deze veronderstelling betekent dat als een covariate verdubbelt het risico van het evenement op één dag, het verdubbelt ook het risico van het evenement op een andere dag.,
proportionele risicomodellen kunnen worden gebruikt voor discrete of continue metingen van de gebeurtenistijd en kunnen tijdafhankelijke covariabelen bevatten (covariabelen waarvan de waarden tijdens de waarnemingsperiode kunnen veranderen). Met behulp van proportionele risico ’s regressie, covariate-adjusted hazard (of risk) ratio’ s kunnen worden geproduceerd.
laten we terugkeren naar de oorspronkelijke vraag gesteld door Arnlov en colleagues…do BMI en metabool syndroom van invloed op de ontwikkeling van hart-en vaatziekten? Lees de Arnlov et al., Impact of Body Mass Index and the Metabolic Syndrome on the Risk of Cardiovascular Disease and Death in Middle Aged Men Circulation 2010; 121; 230-236, met bijzondere aandacht voor de statistische methoden, resultaten en conclusies.
vergelijk en contrast de proportionele risico ‘ s regressiebenadering met een logistische regressiebenadering door Franco et al. Trajecten van het betreden van het metabool syndroom: de Framingham hart studie. Oplage 2009; 120; 1943-1950; oorspronkelijk online gepubliceerd 2 Nov 2009; American Heart Association. 7272 Greenville Avenue, Dallas, TX DOI: 10.,1161 / CIRCULATIONAHA.109.855817
u kunt ook de resultaten van de twee onderzoeken vergelijken. Beide papieren liggen in de Lezingenmap van Week 14.
(toegankelijk vanaf http://www.oxfordjournals.org/our_journals/tropej/online/ma_chap12.pdf)