na de straal en diameter is een ander belangrijk deel van een cirkel een boog. In dit artikel zullen we in detail bespreken wat een boog is, hoe de lengte van een boog te vinden en de meting van een booglengte in radialen. We zullen ook de minor arc en major arc bestuderen.
Wat is een cirkelboog?
een cirkelboog is elk deel van de omtrek van een cirkel. Om te herinneren, de omtrek van een cirkel is de omtrek of afstand rond een cirkel., Daarom kunnen we zeggen dat de omtrek van een cirkel de volledige boog van de cirkel zelf is.
hoe de lengte van een boog te vinden?
De formule voor de berekening van de boog stelt dat:
booglengte = 2nr (θ/360)
waarbij, r = de straal van de cirkel,
π = pi = 3.14
θ = de hoek (in graden) onder een boog in het midden van de cirkel.
360 = de hoek van één volledige rotatie.
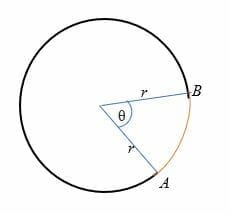
Uit bovenstaande afbeelding is de booglengte (rood getekend) de afstand van punt A tot punt B.,
laten we een paar voorbeeld problemen over de lengte van een boog uit te werken:
Voorbeeld 1
gegeven dat boog AB een hoek van 40 graden naar het midden van een cirkel met een straal van 7 cm. Bereken de lengte van arc AB.
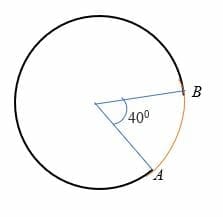
oplossing
gegeven R = 7 cm
θ = 40 graden.
door substitutie,
De lengte van een boog = 2nr(θ/360)
lengte = 2 x 3,14 x 7 x 40/360
= 4,884 cm.
Voorbeeld 2
Zoek de lengte van een boog van een cirkel die een hoek van 120 graden naar het midden van een cirkel met een straal van 24 cm.,
oplossing
De lengte van een boog = 2nr(θ/360)
= 2 x 3,14 x 24 x 120/360
= 50,24 cm.
Voorbeeld 3
De lengte van een boog is 35 m. als de straal van de cirkel 14 m is, zoek dan de hoek onder de boog.
oplossing
De lengte van een boog = 2nr(θ/360)
35 m = 2 x 3,14 x 14 x (θ/360)
35 = 87,92 θ/360
vermenigvuldig beide zijden met 360 om de breuk te verwijderen.
12600 = 87.92 θ
deel beide zijden door 87.92
θ = 143,3 graden.,
Voorbeeld 4
Zoek de straal van een boog die 156 cm lang is en een hoek van 150 graden met het midden van een cirkel onderstelt.
oplossing
De lengte van een boog = 2nr(θ/360)
156 cm = 2 x 3,14 x r x 150/360
156 = 2,6167 R
deel beide zijden door 2,6167
r = 59,62 cm.
De straal van de boog is 59,62 cm.
Hoe vind ik de booglengte in radialen?
er is een verband tussen de hoek die door een boog in radialen wordt ondertrokken en de verhouding tussen de lengte van de boog en de straal van de cirkel., In dit geval
θ =(de lengte van een boog) / (de straal van de cirkel).
daarom wordt de lengte van de boog in radialen gegeven door,
S = R θ
waarbij, θ = hoek onder een boog in radialen
S = lengte van de boog.
r = straal van de cirkel.
een radiaal is de centrale hoek onder een booglengte van één straal, d.w.z. s = r
de radiaal is gewoon een andere manier om de grootte van een hoek te meten. Bijvoorbeeld, om hoeken van graden om te zetten in radialen, vermenigvuldig je de hoek (in graden) met π/180.,
om radialen om te zetten in graden, vermenigvuldig de hoek (in radialen) met 180/π
Voorbeeld 5
Zoek de lengte van een boog met een straal van 10 cm en een hoek van 0,349 radialen.
oplossing
booglengte = R θ
= 0,349 x 10
= 3,49 cm.
Voorbeeld 6
Zoek de lengte van een boog in radialen, die een straal van 10 m en een hoek van 2,356 radialen heeft.
oplossing
booglengte = R θ
= 10 m x 2,356
= 23,56 M.
Voorbeeld 7
Zoek de hoek onder een boog met een lengte van 10,05 mm en een straal van 8 mm.,
oplossing
booglengte = R θ
10.05 = 8 θ
deel beide zijden door 8.
1,2567 = θ
daar is de hoek onder de boog 1,2567 radialen.
Voorbeeld 8
Bereken de straal van een cirkel met een booglengte van 144 yards en een booghoek van 3,665 radialen.
oplossing
booglengte = R θ
144 = 3.665 R
deel beide zijden door 3.665.
144/3. 665 = r
r = 39,29 yards.
Voorbeeld 9
Bereken de lengte van een boog die een hoek van 6.283 radialen Onder het midden van een cirkel met een straal van 28 cm.,
oplossing
booglengte = R θ
= 28 x 6.283
= 175,93 cm
Minor arc (h3)
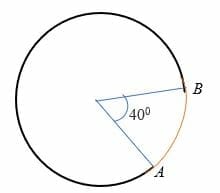
de minor arc is een boog die een hoek van minder 180 graden naar het midden van de cirkel onderstelt. Met andere woorden, de kleine boog meet minder dan een halve cirkel en wordt op de cirkel weergegeven door twee punten. Boog AB in de cirkel hieronder is bijvoorbeeld de kleine boog.
hoofdboog (h3)
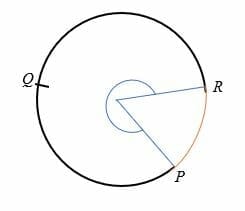
De hoofdboog van een cirkel is een boog die een hoek van meer dan 180 graden ten opzichte van het midden van de cirkel maakt., De hoofdboog is groter dan de halve cirkel en wordt vertegenwoordigd door drie punten op een cirkel.
bijvoorbeeld, PQR is de hoofdboog van de onderstaande cirkel.
oefenproblemen
- Zoek de oppervlakte van de sector van de cirkel met een straal van 9 mm. neem aan dat de hoek onder deze boog in het midden 30 o is.
- Stad A is recht ten noorden van stad B. De breedtegraden van Stad A en stad B zijn respectievelijk 54 O N en 45 O N. Wat is de Noord-Zuid afstand tussen de twee steden? De straal van de aarde is 6400 km.,
<| ol>