Lineær Tilnærming
La oss si at en dag du har glemt en kalkulator, og du virkelig ønsker å finne ut hvordan det kvadratroten av 2 er. Hvordan ville vi finne ut uten kalkulator? Vi kan bruke lineær tilnærming!
Linearisering av en funksjon
linearisering av en funksjon er bare om å finne tangentlinjen av funksjon på et bestemt punkt på en annen måte., Den rettingen formelen er:

hvor L(x) er ligningen for tangenten linje i punkt en.
Hvordan er dette nyttig for oss? Vel, vi kan faktisk bruke denne ligningen til å anslå verdier for funksjonen nærheten punkt en. Ta en titt på denne grafen.,
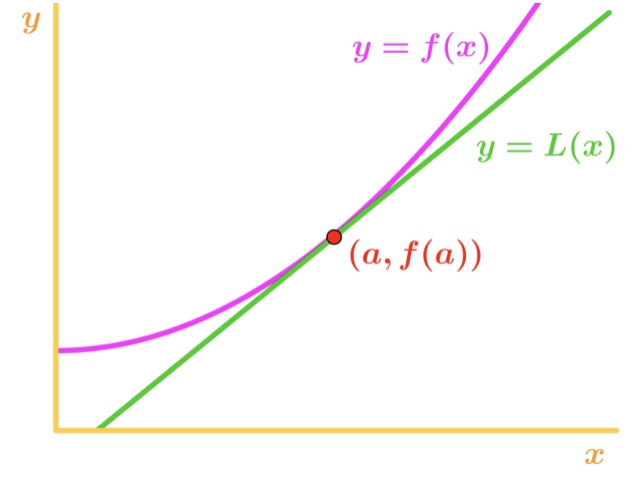
legg Merke til at for x-verdier i nærheten punkt a, ser vi at funksjonen og tangentlinjen er relativt nær hverandre. På grunn av dette, er vi i stand til å skrive at funksjonen er tilnærmet lik tangentlinjen i nærheten punkt en., Med andre ord,

hvor ≈\ca≈ er ca symbolet. Denne ligningen er kjent som lineær tilnærming formel. Det er lineær i en følelse av at tangenten er en rett linje, og vi bruker den til å omtrentlig funksjonen. Ved hjelp av denne tilnærming, er vi i stand til å anslå verdier som ikke gjøres for hånd. For eksempel, kvadratroten av 2 eller naturlige logaritmen av 5 kan alle oppnå!, En viktig ting å merke seg er at denne tilnærming fungerer bare for x-verdier nær et punkt. Hvis du har en x-verdi langt fra punkt a, og deretter tilnærming blir veldig unøyaktig.
Nå kan ikke vi ta en titt på noen eksempler for å finne linearisering av en funksjon, og deretter se på hvordan du bruker lineær approksimasjon!
Finn den linearisering av L(x) for funksjonen på
Spørsmål 1: Vurdere funksjon
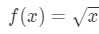
La oss si at vi ønsker å finne linearisering av den funksjonen i punktet a=4.
for Å finne linearisering L(x), husker at

- Trinn 1: Finn en
- Trinn 2: Finn f(a)
- Trinn 3: Finn f'(a).
- Trinn 4: Koble alle tre inn i formelen for å finne L(x)
-
La oss følge disse trinnene!,
Trinn 1: Heldigvis en = 4 er gitt oss i spørsmålet, slik at vi ikke trenger å lete etter det.
- Trinn 2:
legg Merke til at
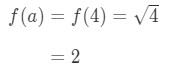
Ligning 1: Linearisering spørsmål pt. 3 - Trinn 3:
Vet at den deriverte av kvadratrøtter er
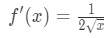
Ligning 1: Linearisering spørsmål pt., 4 And so plugging in x=a gives us:
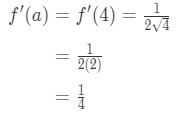
Equation 1: Linearization question pt. 5 - Step 4:
Since we know a, f(a), and f'(a), we can now plug it into L(x) to find the linearization of f(x).
Hence,
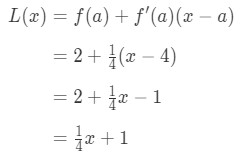
Equation 1: Linearization question pt., 6 Slik at L(x)=14\frac{1}{4}41x+1 er linearisering av denne funksjonen i punktet x=4. I tillegg, det er også tangentlinjen av funksjon i punktet x=4.
Hvordan å gjøre lineær tilnærming
Husk tidligere sa vi at vi kunne bruke ligningen for tangenten linje til omtrentlige verdier av funksjon i nærheten? La oss prøve dette med rettingen vi fant tidligere. Husker at
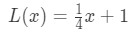
for poeng i nærheten x=4. Vi kan endre dette til en lineær tilnærming til f(x) ved å si at:
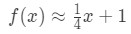
Nå, la oss si at jeg ønsker å omtrentlig f(4.04). Hvis du var å koble dette til den opprinnelige funksjonen, da vil du få 4.04\sqrt{4.04}4.04 . Dette ville være veldig vanskelig å beregne uten en kalkulator., Imidlertid, ved hjelp av lineær tilnærming, kan vi si at

Nå så langt, disse spørsmålene ga oss en funksjon og et poeng å jobbe med. Hva hvis ingen av disse ble gitt til alle? Hva om spørsmålet bare forteller oss å anslå et tall?
Bruke Lineær tilnærming for å anslå et antall
la oss Anta at vi ønsker å anslå 10\sqrt{10}10. Hvordan skulle vi gjøre det?, Vi ville trenge å bruke lineær tilnærming

men vi ikke engang har en funksjon og et poeng å jobbe med. Dette betyr at vi har å gjøre dem selv. Dette leder oss til å gjøre følgende fremgangsmåte:
- Trinn 1: opprette en funksjon
- Trinn 2: opprett et punkt
- Trinn 3: Finn f(a) og f'(a)
- Trinn 4: Koble alt i lineær tilnærming formel
La oss følge trinnene!,
Spørsmål 2: Vurdering 10\sqrt{10}10
- Trinn 1: La oss komme opp med en funksjon. Vær oppmerksom på at vi anslå
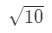
Ligning 3: Estimat med lineær ca. pt.2 Vi må liksom gjøre en sammenheng mellom f(x) og 10\sqrt{10}10. Vi kan ikke si at f(x) = 10\sqrt{10}10 fordi funksjonen vil ikke være avhengig av x. Så hvorfor kan ikke vi gjøre dette? La
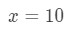
Ligning 3: Estimat med lineær ca. pt.,3 Hvis vi gjør det, så vi er i utgangspunktet sa:
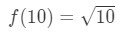
Ligning 3: Estimat med lineær ca. pt.4 nå kan Vi selvsagt si hva som funksjon bør være. La
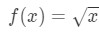
Ligning 3: Estimat med lineær ca. pt.5 Slik at vi har en funksjon, men nå trenger vi et punkt a til å jobbe med.,
- Trinn 2:
– tasten for å finne riktig verdi a er ved å tenke på to ting:
1) Kontroller at verdien er en nær x
2) Kontroller at f(a) er et fint antall.
Ville en = 8 være tilstrekkelig nok? Vel, 8 er ganske nær til 10 så det er ikke dårlig. Imidlertid,
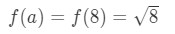
Ligning 3: Estimat med lineær ca. pt.6 legg Merke til at 8\sqrt{8}8 er ikke en veldig fin antall. Faktisk, du får en haug av desimaltall. Så må vi prøve noe annet.,
Vil a = 9 være tilstrekkelig nok? Igjen, 9 er ganske nær til 10 så er det greit. Også,

Ligning 3: Estimat med lineær ca. pt.7 f(a) er faktisk en fin hele tall her, så dette faktisk fungerer! Så plukke en=9 er tilstrekkelig nok.
- Trinn 3:
vær Oppmerksom på at fra tidligere:

Ligning 3: Estimat med lineær ca. pt.,8 Calculating f'(x) we have again:

Equation 3: Estimate with linear approx. pt.9 So
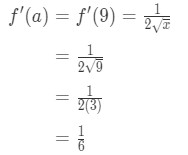
Equation 3: Estimate with linear approx. pt.,10 - Step 4:
Going back to the linear approximation formula we have:

Equation 3: Estimate with linear approx. pt.11 Plugging a, f(a), f'(a), f(x), and x in our formula you will see that:

Equation 3: Estimate with linear approx. pt.12 Hence, we just approximated the number!,
Hvis du ønsker mer praksis problemer om lineær tilnærming, så jeg anbefaler deg å se på denne linken her.
http://tutorial.math.lamar.edu/Classes/CalcI/LinearApproximations.aspx
Overvurdere og Undervurdere
Vi vet at lineær tilnærming er bare en estimering av funksjon verdi på et angitt punkt. Men hvordan vet vi at hvis vi mener er en overvurdere eller undervurdere? Vi beregne den andre deriverte og se på concavity.,
Konkave opp vs Konkave ned
Dersom den andre deriverte av funksjonen er større enn 0 for verdiene i nærheten av en, og deretter funksjonen er konkav opp. Dette betyr at vår tilnærming vil være lavt. Med andre ord,
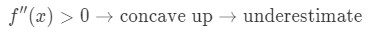
Hvorfor? La oss ta en titt på denne grafen.,
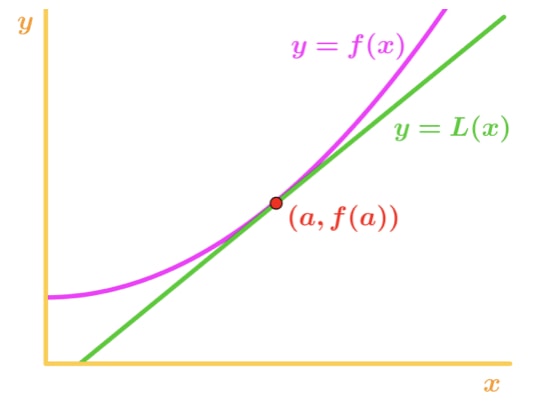
legg Merke til at f(x) er konkav oppover og tangentlinjen er rett under f(x). La oss si var å bruke tangentlinjen til å anslå f(x). Deretter y-verdiene til tangentlinjen er alltid kommer til å være mindre enn den faktiske verdien av f(x). Vi har derfor et undervurdere
Nå, hvis den andre deriverte av funksjonen er mindre enn 0 for verdiene i nærheten av en, og deretter funksjonen er konkav nedover., Dette betyr at vår tilnærming vil være en overvurdere. Med andre ord,
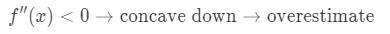
Igjen, hvorfor? La oss ta en titt på et annet diagram.
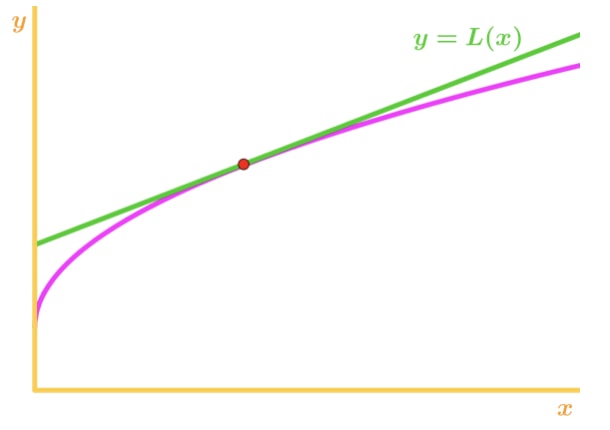
legg Merke til at f(x) er konkav nedover, og tangerer linjen er rett ovenfor f(x). Igjen, la oss si at vi kommer til å bruke tangentlinjen til å anslå f(x)., Deretter y-verdiene til tangentlinjen er alltid kommer til å være større enn den faktiske verdien av f(x). Vi har derfor en overvurdere.
Så hvis du noen gang trenger å se hvis verdien er en undervurdering eller en overestimation, sørg for at du følger disse trinnene:
- Trinn 1: Finn andre avledede
- Trinn 2: se på concavity av funksjon i nærheten av et punkt
- Trinn 3: Bekreft at det er en undervurdere/overvurdere
La oss ta en titt på et eksempel:
Spørsmål 3: La f(x) = x\sqrt{x}x og a = 4. Hvis vi lineær omtrentlig f(4.,04), ville det være en overvurdere eller undervurdere?
- Trinn 1: Se at
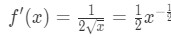
Ligning 4: Overvurdere spørsmål pt.1 Så den andre deriverte er
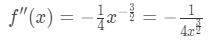
Ligning 4: Overvurdere spørsmål pt.2 - Trinn 2:
legg Merke til at a=4, så vi ønsker å se på positive verdier av x 4 nærheten. Nå se på den andre deriverte., Når x er positiv, ser vi at
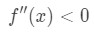
Ligning 4: Overvurdere spørsmål pt.3 Derfor, det er konkav ned
- Trinn 3:
– Vi vet at hvis funksjonen er konkav nedover, så tangentlinjen vil være over-funksjon. Derfor, ved hjelp av tangentlinjen som en tilnærming vil gi en overvurdert verdi.
Differensialer
Ikke bare kan vi omtrentlige verdier med lineær tilnærming, men vi kan også omtrentlige med differensialer., For å simulere, bruker vi følgende formel
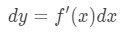
hvor dy og dx er differensialer, og f'(x) er den deriverte av f i form av x. Siden vi har å gjøre med svært små endringer i x og y, så vi kommer til å bruke det faktum at:
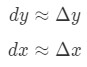
Imidlertid er de fleste av de spørsmålene vi gjøre innebære innstillingen
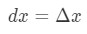
Så å bruke disse fakta vil lede oss til å ha:
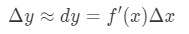
Denne tilnærming er svært nyttig når du nærmer endring av y., Holde i sinnet tilbake da de ikke har kalkulatorer, så dette er den beste tilnærming kan de få for funksjoner med kvadratrøtter eller naturlige logaritmer.
de Fleste av den tiden du er nødt til å se for f'(x) og Δ\DeltaΔx deg selv. Med andre ord, følger du disse trinnene for å omtrentlig Δ\DeltaΔy!
- Trinn 1: Finn Δ\DeltaΔx
- Trinn 2: Finn f'(x)
- Trinn 3: Koble alt inn i formelen for å finne dy. dy vil være tilnærming for Δ\DeltaΔy.
La oss se på et eksempel på bruk av denne tilnærming:
Spørsmål 4: Vurdere funksjonen y = ln(x + 1)., Anta at x endres fra 0 til 0,01. Omtrentlig Δ\DeltaΔy.
- Trinn 1: legg Merke til at x-endringer fra 0 til 0,01, slik at endringen i x vil være:
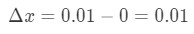
Ligning 6: Differensial spørsmål pt.1 - Trinn 2:
derivatet ville være:
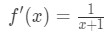
Ligning 6: Differensial spørsmål pt.,2 - Trinn 3:
Koble alt vi har:
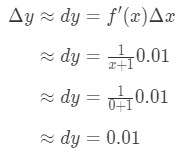
Ligning 6: Differensial spørsmål pt.3 Derfor, Δ\DeltaΔy ≈\ca≈ 0.01
Men, mesteparten av tiden vi ønsker å estimere en verdi av funksjon, og ikke endring av verdien. Derfor vil vi legge til begge sider av ligningen med y, som gir oss:
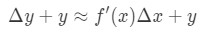
som er det samme som:
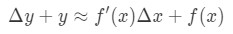
Denne ligningen er litt vanskelig å lese på, så vi kommer til å omorganisere det enda mer. La oss prøve å bli kvitt y og Δ\DeltaΔy. Legg merke til at Δ\DeltaΔy+ y er i utgangspunktet det samme som å finne verdien av funksjonen Δ\DeltaΔx+x. Med andre ord,
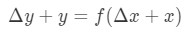
Derfor å erstatte dette i vår tilnærming ovenfor vil gi oss:
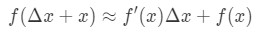
hvor f(Δ\DeltaΔx+x) er verdien vi prøver å anslå. Hvordan bruker vi denne formelen? Jeg anbefaler følgende fremgangsmåte:
La oss bruke disse trinnene for følgende spørsmål.
Spørsmål 5: Bruk differensialer å omtrentlig 10\sqrt{10}10.
- Trinn 1: Sammenlign f(Δ\DeltaΔx+x) med 10\sqrt{10}10., Since 10\sqrt{10}10 has a square root and 9 is a perfect square that is closest to 10, then let
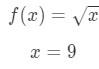
Equation 7: Approximate value with differentials pt.1 Notice that:
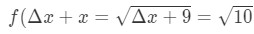
Equation 7: Approximate value with differentials pt.,2 Se at det er ikke noe annet valg enn å la Δ\DeltaΔx = 1
- Trinn 2:
Se at den deriverte gir:

Ligning 7: en Omtrentlig verdi med differensialer pt.3 Så, dette innebærer
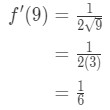
Ligning 7: en Omtrentlig verdi med differensialer pt.,4 - Trinn 3:
Plugging alt inn i formelen får vi:
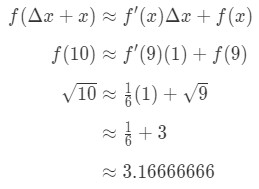
Ligning 7: en Omtrentlig verdi med differensialer pt.5 Derfor, vi har akkurat rundet antall.
En interessant ting å merke seg er at lineær tilnærming og differensialer både gi samme resultat for 10\sqrt{10}10.,
Hvis du ønsker å lære mer om differensialer, klikk på denne linken:
http://tutorial.math.lamar.edu/Classes/CalcI/LinearApproximations.aspx
Beviser L ‘ hospital i barcelona, er Regelen ved hjelp av lineær tilnærming
Nå har vi lært mye om lineær tilnærming, men hva annet kan vi gjøre med det? Vi kan faktisk bruke lineær tilnærming formel for å bevise en regel kjent som L ‘ hospital i barcelona Regelen . Her er hvordan bevis fungerer.
Husker at lineær tilnærming formelen er:

Se at vi kan omorganisere formel slik at:
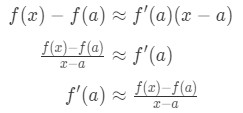
Innse at tilnærming blir mer og mer nøyaktige som vi plukke x-verdier som er nærmere en. Med andre ord, hvis vi tar den grense som x→a, så vil de like. Så
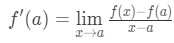
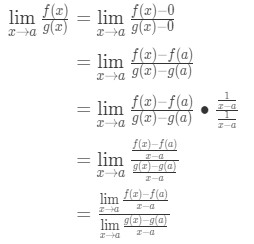
Nå ser at vi kan bruke formelen som vi utledet tidligere høyre her. Så nå
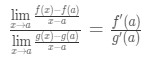
Nå i stedet for å skrive f'(a) og g'(a), kan vi bruke grenser som x→a (fordi vi vet at f og g er differensiable)., Så
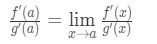
Derfor, vi bare viste at:
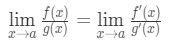
som er L ‘ hospital i barcelona Regelen .
Ved å bruke l’hopital regelen
Vi alltid ønsker å bruke l’hoptial regelen når vi støter på ubestemt grenser. Det er to typer av ubestemte former., Disse ubestemte formene vil være:
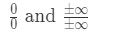
mange mennesker gjør feil av ved hjelp av l’hopital er regelen, selv uten å sjekke om det er en ubestemt grense. Så sørg for at du sjekker den første! Ellers vil det ikke fungere, og du vil få feil svar. Her er en guide til å bruke l’hopital regelen:
- Trinn 1: Vurdere grensen direkte.
- Trinn 2: Sjekk om det er en av de ubestemte former. Hvis det er det, går du til trinn 3.,
- Trinn 3: Bruke l’hopital regelen.
- Trinn 4: Kontroller om du kan få en annen ubestemt form. Gjenta Trinn 3 hvis du gjør det.
La oss ta en titt på et par eksempler ved hjelp av disse trinnene.
Spørsmål 6: Evaluering grensen
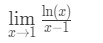
- Trinn 1: Vurdering grensen direkte gir oss
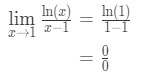
Ligning 9: L’hopital regelen spørsmål pt.,2 - Trinn 2:
Ja, det er en av de ubestemte former.
- Trinn 3:
Søker l’hopital er regel vi har:
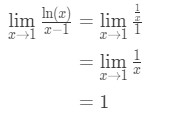
Ligning 9: L’hopital regelen spørsmål pt.3 - Trinn 4:
en er ikke en ubestemt form, så er vi ferdig og svaret er 1.
Nå er det spørsmålet var litt lett, så hvorfor ikke vi ta en titt på noe som er litt vanskeligere.,
Spørsmål 7: Evaluering grensen
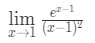
- Trinn 1: Vurdering grensen direkte ser vi at:
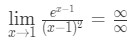
Ligning 10: L’hopital regelen to ganger spørsmålet pt.2 - Trinn 2:
Dette er et ubestemt form, så går du til trinn 3.,
- Trinn 3:
Søker l’hopital er regel vi har
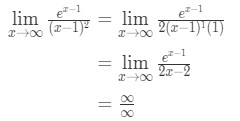
Ligning 10: L’hopital regelen to ganger spørsmålet pt.3 - Trinn 4:
Dette er en annen ubestemt form. Så vi må gå tilbake til trinn 3, og gjelder l’hoptial regler igjen.
- Trinn 3:
Søker l’hopital regelen igjen har vi:
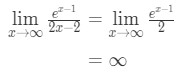
Ligning 10: L’hopital regelen to ganger spørsmålet pt.,4 - Trinn 4:
Infinity er ikke en ubestemt form, så er vi ferdig og svaret er ∞\infty∞