supongamos que desea considerar el impacto de un factor de riesgo en el tiempo hasta la ocurrencia de un evento. Por ejemplo, Arnlov et al (2010) consideran el impacto del índice de masa corporal (IMC) y el síndrome metabólico en el desarrollo de enfermedades cardiovasculares y muerte en hombres de mediana edad. Las asociaciones se investigaron utilizando datos de un estudio de cohorte de 1758 hombres suecos de mediana edad que residían en un condado con más de 30 años de seguimiento., La figura siguiente representa el tiempo hasta un evento cardiovascular mayor por categoría de IMC y presencia (B) o ausencia (a) de síndrome metabólico. ¿Hay alguna diferencia en estas curvas de supervivencia?
Figura 2: curvas de Kaplan-Meier para eventos cardiovasculares mayores en diferentes categorías de IMC en individuos sin Met (A) y con met (B).
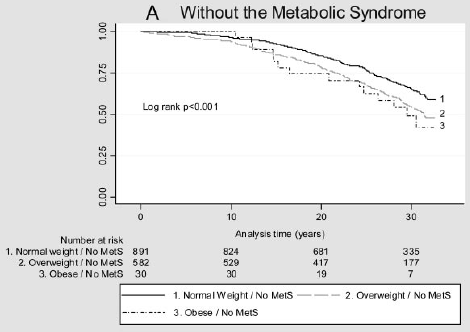
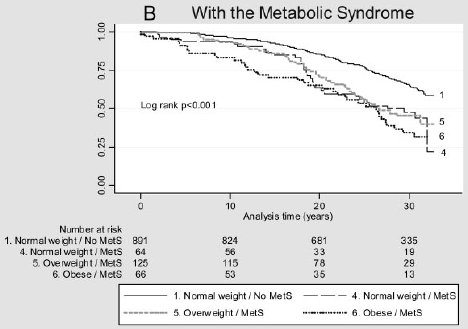
(Figuras reproducidas de Arnlov, J et al., Impacto del índice de masa corporal y el síndrome metabólico en el riesgo de enfermedad Cardiovascular y muerte en hombres de mediana edad. Circulation 2010; 121; 230-236, originalmente publicado en línea 28/12/2009; DOI 10.1161 / CIRCULATIONAHA.109,88752)
la ocurrencia de un evento cardiovascular mayor es una respuesta binaria. ¿Sería apropiada la regresión logística, con el IMC como variable predictora, para analizar estos datos?,
respuesta
La relación entre la presencia o ausencia de un evento cardiovascular mayor y la variable predictora podría ser evaluada con regresión logística en un momento determinado, pero esto no compararía directamente las curvas de supervivencia. Un análisis de supervivencia compararía las curvas en base al tiempo del evento.
los métodos de análisis de supervivencia, como la regresión de riesgos proporcionales, difieren de la regresión logística al evaluar una tasa en lugar de una proporción.,
regresión logística en contraste, considera la proporción de nuevos casos que se desarrollan en un período de tiempo dado, es decir, la incidencia acumulada., La regresión logística estima el odds ratio; la regresión de riesgos proporcionales estima el hazard ratio.
la relación de funciones de riesgo puede considerarse una relación de funciones de riesgo, por lo que el modelo de regresión de riesgos proporcionales puede considerarse una función del riesgo relativo (mientras que los modelos de regresión logística son una función de una relación de probabilidades). Los cambios en una covariable tienen un efecto multiplicativo sobre el riesgo basal. El modelo en términos de la función de peligro en el tiempo t ES:
\(\lambda \ left (t / x_{1i}, X_{2i},…, X_{Ki} \right )=\lambda_{0} (t)exp\left ( \beta_{1}X_{1i}+\beta_{2}X_{2i}+…,+\beta_{K}X_ {Ki} \ right)\)
aunque no se selecciona ningún modelo de probabilidad particular para representar los tiempos de supervivencia, la regresión de riesgos proporcionales tiene una suposición importante: el riesgo para cualquier individuo es una proporción fija del riesgo para cualquier otro individuo. (es decir, riesgos proporcionales)., Observe si \(\lambda_0 (t)\) es la función de riesgo para un sujeto con todos los valores predictores iguales a cero y \(\lambda_1 (t)\) es la función de riesgo para un sujeto con otros valores para las variables predictoras, entonces la razón de riesgo depende solo de las variables predictoras y no del tiempo t. esta suposición significa que si una covariable duplica el riesgo del evento en el primer día, también duplica el riesgo del evento en cualquier otro día.,
los modelos de riesgos proporcionales se pueden utilizar para medidas discretas o continuas del tiempo del evento y pueden incorporar covariables dependientes del tiempo (covariables cuyos valores pueden cambiar durante el período de observación). Utilizando la regresión de riesgos proporcionales, se pueden producir ratios de riesgo (o riesgo) ajustados por covariables.
volvamos a la pregunta original planteada por Arnlov y colleagues…do ¿el IMC y el síndrome metabólico afectan el desarrollo de la enfermedad cardiovascular? Lea el Arnlov et al., Impacto del índice de masa corporal y el síndrome metabólico en el riesgo de enfermedad Cardiovascular y muerte en varones de mediana edad circulación 2010; 121;230-236, prestando especial atención a los métodos estadísticos, resultados y conclusiones.
comparar y contrastar el enfoque de regresión de riesgos proporcionales con un enfoque de regresión logística mediante la lectura de Franco et al. Trayectories of Entering the Metabolic Syndrome: the Framingham Heart Study. Circulación 2009;120; 1943-1950; publicado originalmente en línea Nov 2, 2009; American Heart Association. 7272 Greenville Avenue, Dallas, TX DOI: 10.,1161 / CIRCULATIONAHA.109.855817
también puede comparar los resultados de los dos estudios. Ambos artículos están en la carpeta lecturas de la Semana 14.
(accedido desde http://www.oxfordjournals.org/our_journals/tropej/online/ma_chap12.pdf)