반지름과 지름 다음에 원의 또 다른 중요한 부분은 원호입니다. 이 문서에서,우리는 우리 것에 대해 논의 정보는 무엇 호,하는 방법을 찾기 위한 길이의 아크 및 측정의 아크 길이는 라디안입니다. 우리는 또한 마이너 아크와 메이저 아크에 대해 연구 할 것입니다.
원의 호는 무엇입니까?
원의 호는 원의 원주의 임의의 부분이다. 회상하기 위해 원의 둘레는 원 주위의 둘레 또는 거리입니다., 따라서 우리는 원의 둘레가 원 자체의 전체 호라고 말할 수 있습니다.
호의 길이를 찾는 방법은 무엇입니까?
에 대한 공식을 계산하는 호국:
호 길이=2πr(θ/360)
어디서,r=radius 의 원형
π=pi=3.14
θ=각도(도)subtended 에 의해 호의 중심에 원입니다.
360=하나의 완전한 회전 각도.
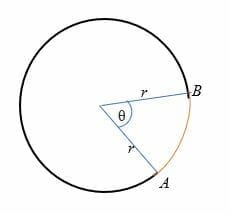
에서 위의 그림이 길이의 아크(에 그려진 레드)에서의 거리트,
의 작업을 몇 가지 예시 문제에 대한 길이의 아크:
예제 1
주어진 것 아크 AB subtends 각도의 40 도의 중심에 원의 반지름이 7 센티미터. 아크 ab 의 길이를 계산하십시오.
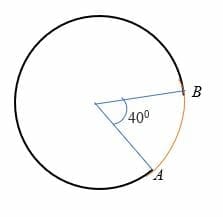
솔루션
주어진 r=7cm
θ=40 도.
치환에 의해,
호의 길이=2nr(θ/360)
길이=2×3.14x7x40/360
=4.884cm.
실시예 2
반지름이 24cm 인 원의 중심에 120 도의 각도를 서브 텐션하는 원의 호의 길이를 찾습니다.,
솔루션
의 길이 호=2πr(θ/360)
=2×3.14x24x120/360
=50.24cm.
예 3
원의 길이가 35m 인 경우 원의 반지름이 14m 인 경우 원호에 의해 subtended 각도를 찾습니다.
솔루션
의 길이 호=2πr(θ/360)
35m=2×3.14x14x(θ/360)
35=87.92θ/360
곱으로 양쪽 360 을 제거하는 부분이다.
12600=87.92θ
양쪽을 87.92
θ=143.3 도로 나눕니다.,
예 4
길이가 156cm 이고 원의 중심에 150 도 각도를 서브 텐션하는 호의 반경을 찾습니다.
솔루션
의 길이 호=2πr(θ/360)
156cm=2×3.14x r x150/360
156=2.6167r
나누는 양쪽 모두에 의해 2.6167
r=59.62cm.따라서 원호의 반경은 59.62cm 입니다.
라디안에서 호 길이를 찾는 방법은 무엇입니까?
관계가 있는 사이 각도 subtended 호에 의해에 라디안과의 비율이 호의 길이를 원의 반경., 이 경우
θ=(호의 길이)/(원의 반경).
그러므로,길이의 아크 라디안 에 의해 주어진,
S=r θ
어디서,θ=각 subtended 호에 의해에 라디안
S=길이의 아크입니다.
r=원의 반지름.
한 radian 중앙 각 subtended 에 의해 호의 길이 하나의 반경이 즉 s=r
방은 다른 방법으로 측정 크기의 수도 있습니다. 예를 들어 각도를도에서 라디안으로 변환하려면 각도(도)에 π/180 을 곱하십시오.,
마찬가지로 변환하는 라디안을 도,곱 angle(라디안)의 180/π
예 5
을 찾기 위한 길이의 아크의 반경이 10cm 및 각 subtended 은 0.349 라디안입니다.
용액
아크 길이=r θ
=0.349×10
=3.49cm.
실시예 6
반지름이 10m 이고 각도가 2.356 라디안인 라디안 단위의 원호 길이를 찾습니다.
솔루션
호 길이=r θ
=10m x2.356
=23.56m.
예 7
각도를 찾을 subtended 에 의해 호의 10.05mm radius of8mm.,
용액
아크 길이=r θ
10.05=8θ
양쪽을 8 로 나눕니다.
1.2567=θ
거기에서 호에 의해 subtended 각도는 1.2567 라디안입니다.
실시예 8
원호 길이가 144 야드이고 원호 각도가 3.665 라디안인 원의 반지름을 계산합니다.
솔루션
호 길이=r θ
144=3.665r
나누는 양쪽 모두에 의해 3.665.
144/3.665=r
r=39.29 야드.
예 9
의 길이를 계산하는 아크는 subtends 각도의 6.283 라디안의 중심에 원 radius28cm.,
솔루션
호 길이=r θ
=28×6.283
=175.93cm
부크(h3)
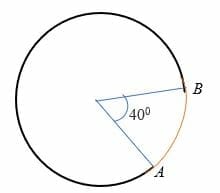
부크 호는 subtends 각도의 더 적은 180 도의 중심에 원입니다. 즉,마이너 호는 반원보다 적게 측정되며 원에 두 점으로 표시됩니다. 예를 들어,아래 원의 아크 AB 는 마이너 호입니다.
주요크(h3)
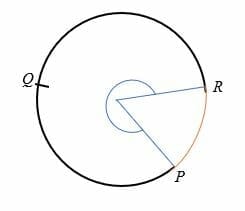
주요 개의 것 아크는 subtends 의 각도보다 더 많은 180 도의 중심에 원입니다., 주요 호는 반원보다 크며 원의 세 점으로 표시됩니다.
예를 들어,pqr 은 아래 표시된 원의 주요 호입니다.
연습 문제
- 의 영역을 찾을 수 있 부문의의 원 radius9mm. 가정 각도 subtended 이크 센터에서 30o.
- 시로 인해 북한의 도시 B. 도의 도시와 도시 B54o N45o N 각각합니다. 두 도시 사이의 남북 거리는 얼마입니까? 지구의 반경은 6400 킬로미터입니다.,