線形近似
ある日、電卓を忘れてしまったとしましょう。2の平方根がどのようになっているかを本当に見つけたいとしましょう。 どのように我々は電卓なしで見つけるだろうか? 線形近似を使うことができます!
関数の線形化
関数の線形化は、特定の点における関数の接線を別の方法で見つけることです。, 線形化式は次のとおりです。

ここで、L(x)は点aにおける接線の方程式です。
これはどのように役立ちますか? この方程式を使って点aの近くの関数の値を近似することができますこのグラフを見てください,
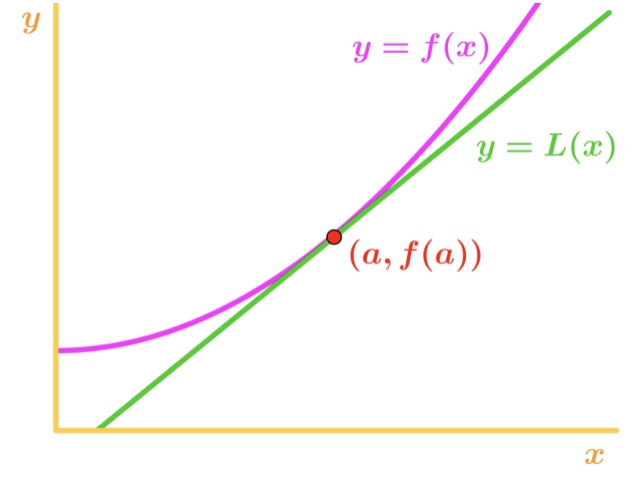
点aの近くのx値については、関数と接線が比較的近いことに注意してください。 このため、関数は点aの近くの接線にほぼ等しいと書くことができます。, つまり、

ここで、θ\approx θは約記号です。 この方程式は線形近似式として知られています。 接線が直線であり、関数を近似するためにそれを使用しているという意味で線形です。 この近似を使用すると、手作業ではできない値を近似することができます。 たとえば、2の平方根または5の自然対数はすべて近似することができます!, 注意すべき重要なことは、この近似は点aの近くのx値に対してのみ機能することです。x値が点aから遠い場合、近似は本当に不正確になります。
ここでは、関数の線形化を見つけるいくつかの例を見て、線形近似を使用する方法を見てはいけません!
関数のl(x)の線形化を見つける
質問1:関数を考えてみましょう
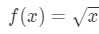
ポイントa=4での関数の線形化を求めたいとしましょう。
線形化L(x)を見つけるには、次のことを思い出してください

- ステップ1:Aを見つける
- ステップ2:F(a)を見つける
- ステップ3:F’(a)を見つける。
- ステップ4:L(x)を見つけるために三つのすべてを式に差し込みます
-
これらの手順に従ってみましょう!,
ステップ1:幸いにもa=4が質問で私たちに与えられているので、それを探す必要はありません。
- ステップ2:
それに注意してください
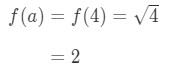
式1:線形化の質問pt。 3 - ステップ3:
平方根の導関数があることを知っている
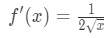
式1:線形化の質問pt。, 4 And so plugging in x=a gives us:
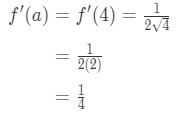
Equation 1: Linearization question pt. 5 - Step 4:
Since we know a, f(a), and f'(a), we can now plug it into L(x) to find the linearization of f(x).
Hence,
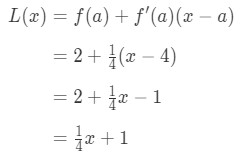
Equation 1: Linearization question pt., 6 したがって、L(x)=14\frac{1}{4}41x+1は、点x=4におけるこの関数の線形化です。 さらに、それは点x=4における関数の接線でもあります。
線形近似を行う方法
以前、接線の方程式を使用してaの近くの関数の値を近似できると言ったことを覚えておいてください。 先ほど見つけた線形化でこれを試してみましょう。 それを思い出してください
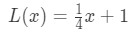
x=4の近くの点について。 これをf(x)の線形近似に変更するには、次のようにします。
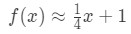
さて、f(4.04)を近似したいとしましょう。 これを元の関数にプラグインすると、4.04\sqrt{4.04}4.04が得られます。 これは電卓なしで計算するのは本当に難しいでしょう。, しかし、線形近似を使用して、我々はそれを言うことができます

これまでのところ、これらの質問は私たちに機能と作業するポイントを与えました。 これらのどれも全然与えられなかったら何か。 質問が数字を推定するように指示するだけの場合はどうなりますか?
数値を推定するために線形近似を使用します
10\sqrt{10}10を推定したいとします。 どうすればいいですか?, 私たちは、線形近似を使用する必要があります

しかし、機能と機能するポイントさえありません。 することこそ、重要であり、これについています。 これにより、次の手順が実行されます。
- ステップ1:関数を作成します。
- ステップ2:点aを作成します。
- ステップ3:f(a)とf'(a)を見つけます。
- ステップ4:すべてを線形近似式にプラグインします。
ステップに従ってください。,
質問2:推定10\sqrt{10}10
- ステップ1:関数を考え出しましょう。 私たちは推定していることに注意してください
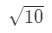
式3:線形約で推定します。 pt.2 何らかの形でf(x)と10\sqrt{10}10の関係を作る必要があります。 関数はxに依存しないため、f(x)=10\sqrt{10}10とは言えません。 Let
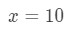
式3:線形約で推定します。 pt.,3 それを行うと、基本的には
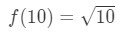
式3:線形約で推定します。 pt.4 これで、関数がどうあるべきかを明らかに伝えることができます。 Let
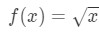
式3:線形約で推定します。 pt.5 だから私たちは関数を持っていますが、今私たちはで動作するポイントaが必要です。,
- ステップ2:
正しい値aを見つけるための鍵は、二つのことを考慮することです:
1)値aがxに近いことを確認してください
2)f(a)が素敵な数であるこ
a=8で十分でしょうか? まあ、8はかなり10に近いので悪くはありません。 ただし、
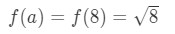
式3:線形約で推定します。 pt.6 8\sqrt{8}8はあまり良い数ではないことに注意してください。 実際には、小数の束を取得します。 しておりますので試してみません。,
a=9で十分でしょうか? 繰り返しますが、9は10にかなり近いので大丈夫です。 また、

式3:線形約で推定します。 pt.7 f(a)は実際にはここで素敵な整数なので、これは実際に動作します! したがって、a=9を選ぶだけで十分です。
- ステップ3:
以前からのことに注意してください:

式3:線形約で推定します。 pt.,8 Calculating f'(x) we have again:

Equation 3: Estimate with linear approx. pt.9 So
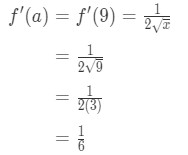
Equation 3: Estimate with linear approx. pt.,10 - Step 4:
Going back to the linear approximation formula we have:

Equation 3: Estimate with linear approx. pt.11 Plugging a, f(a), f'(a), f(x), and x in our formula you will see that:

Equation 3: Estimate with linear approx. pt.12 Hence, we just approximated the number!,
線形近似についてもっと練習問題が必要な場合は、こちらのリンクを見ることをお勧めします。
http://tutorial.math.lamar.edu/Classes/CalcI/LinearApproximations.aspx
過大評価と過小評価
線形近似は、指定された点での関数の値の推定に過ぎないことがわかります。 しかし、私たちの見積もりが過大評価または過小評価である場合、どのようにしてそれを知ることができますか? 二次導関数を計算し、凹部を見ます。,
凹アップ対凹ダウン
関数の二次導関数がaの近くの値に対して0より大きい場合、関数は凹アップです。 これは、私たちの近似が過小評価されることを意味します。 言い換えれば、
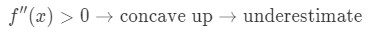
なぜ? このグラフを見てみましょう。,
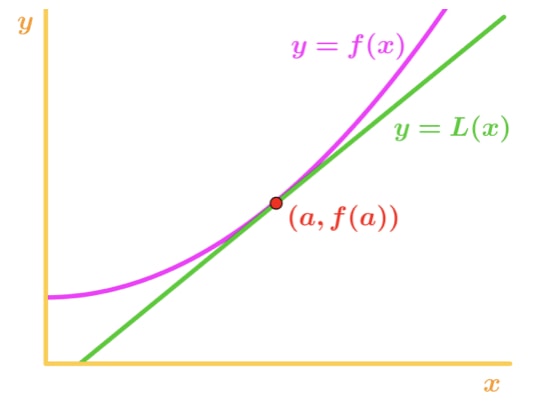
f(x)が凹状であり、接線がf(x)のすぐ下にあることに注意してください。 接線を使ってf(x)を近似するとしましょう。 次に、接線のy値は常にf(x)の実際の値よりも小さくなります。 したがって、我々は過小評価を持っています
関数の二次導関数がaの近くの値に対して0未満の場合、関数は凹状になります。, これは、私たちの近似が過大評価されることを意味します。 言い換えれば、
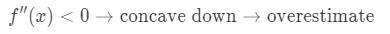
再び、なぜ? 別のグラフを見てみましょう。
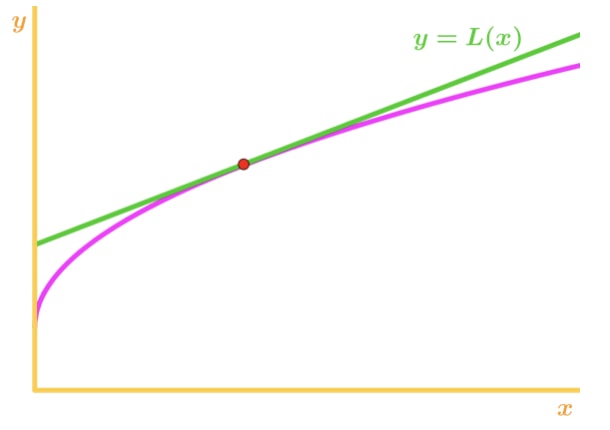
f(x)は凹状であり、接線はf(x)のすぐ上にあることに注意してください。 繰り返しますが、接線を使用してf(x)を近似するとしましょう。, 次に、接線のy値は常にf(x)の実際の値よりも大きくなります。 したがって、私たちは過大評価しています。ステップ1:二次導関数を見つける
例を見てみましょう:
質問3:(x)=x\sqrt{x}xおよびa=4. もし線形近似f(4.,04)、それは過大評価または過小評価でしょうか?
- ステップ1:それを参照してください
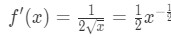
式4:質問ptを過大評価します。1 したがって、二次導関数は
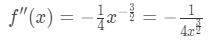
式4:質問ptを過大評価する。2 - ステップ2:
a=4であることに注意してくださいので、4の近くのxの正の値を見たいと思います。 今二次導関数を見てください。, Xが正であるとき、我々はそれを参照してください
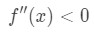
式4:質問ptを過大評価。3 したがって、それは凹状です
- ステップ3:
関数が凹状であれば、接線は関数の上になることがわかります。 したがって、接線を近似として使用すると、過大評価された値が得られます。
微分
線形近似で値を近似することができるだけでなく、微分で近似することもできます。, 近似するために、次の式を使用します
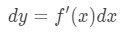
ここで、dyとdxは微分であり、f'(x)はxに関するfの導関数です。xの非常に小さな変化を扱っているので、xの非常に小さな変化を扱っているので、xの非常に小さな変化を扱っているので、Xの非常に小さな変化を扱っているので、Xの非常に小さな変化を扱っているので、F'(x)はxに関する微分です。そしてy、その後、我々は事実を使用しようとしている:
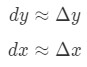
ただし、ほとんどの質問では、
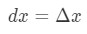
これらの事実を使用すると、次のようになります。
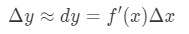
この近似は、yの変化を近似するときに非常に便利です。, 当時彼らは電卓を持っていなかったので、これは平方根や自然対数を持つ関数に対して得ることができる最良の近似です。ほとんどの場合、f’(x)とΔ\DeltaΔxを自分で探す必要があります。 言い換えれば、Δ\DeltaΔyを近似するには、次の手順に従います。
- ステップ1:Δ\DeltaΔxを見つける
- ステップ2:f’(x)を見つける
- ステップ3:すべてを式に差し込んでdyを見つけます。 dyはΔ\DeltaΔyの近似になります。
この近似を使用する例を見てみましょう:
質問4:関数y=ln(x+1)を考えてみましょう。, Xが0から0.01に変化するとします。 おおよそΔ\DeltaΔy。
- ステップ1:xが0から0.01に変化することに注意してください。xの変化は次のようになります。
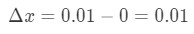
式6:差分質問pt。1 - ステップ2:
微分は次のようになります。
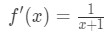
式6:差分質問pt。,2 - ステップ3:
私たちが持っているすべてのものを差し込む:
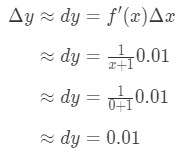
式6:差分質問pt。3 したがって、Δ\DeltaΔy≤\approx≤0.01
しかし、ほとんどの場合、値の変化ではなく、関数の値を推定したいと考えています。 したがって、方程式の両側をyで追加します。
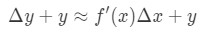
と同じです:
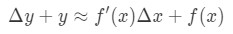
この式は少し読みにくいので、さらに再配置します。 YとΔ\DeltaΔyを取り除こうとしましょう。 つまり、
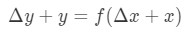
したがって、上記の近似でこれを代入すると、次のようになります。
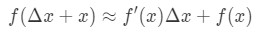
ここで、f(Δ\DeltaΔx+x)は推定しようとしている値です。 この式をどのように使用するのですか? 私はこれらの手順に従うことをお勧めします:
次の質問にこれらの手順を使用しましょう。質問5:微分を使用して10\sqrt{10}10を近似します。ステップ1:f(Δ\DeltaΔx+x)を10\sqrt{10}10と比較します。, Since 10\sqrt{10}10 has a square root and 9 is a perfect square that is closest to 10, then let
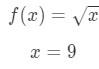
Notice that:
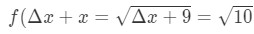
Δ\DeltaΔx=1
導関数が与えることを確認してください:

したがって、これは
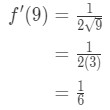
すべてを式に差し込むと、
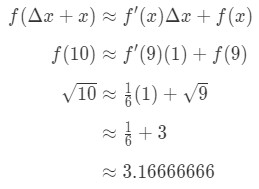
したがって、数値を近似しました。
注目すべき興味深いことは、線形近似と微分の両方が10\sqrt{10}10に対して同じ結果を与えるということです。,
微分についてもっと知りたい場合は、このリンクをクリックしてください。
http://tutorial.math.lamar.edu/Classes/CalcI/LinearApproximations.aspx
線形近似を使用してL’Hospitalのルールを証明する
今、私たちは線形近似について多くのことを学びましたが、他に何ができますか? 実際には、線形近似公式を使用して、L’Hospitalの規則として知られている規則を証明することができます。 証明の仕組みは次のとおりです。
線形近似式は次のとおりであることを思い出してください。

次のように式を並べ替えることができることを確認してください。
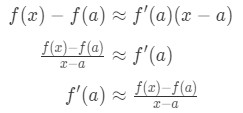
近似は、aに近いx値を選択するにつれてますます正確になることを認識してください。 だから
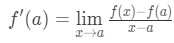
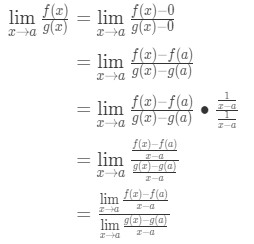
ここで、先ほど導出した式を適用できることに注意してください。 だから今
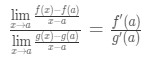
これで、f'(a)とg'(a)を書く代わりに、x→aとして制限を適用できます(fとgが微分可能であることがわかっているため)。, したがって、
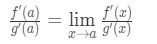
したがって、我々はちょうどそれを示した:
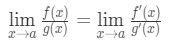
これはl’hospitalのルールです。
l’hopitalのルールを使用する場合
不確定な制限に遭遇したときは、常にl’hopitalのルールを適用します。 不定形には二つのタイプがあります。, これらの不確定なフォームは次のようになります。
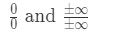
多くの人々は、それが不確定な制限であるかどうかをチェックせずにl’hopitalのルールを使用する間違いを犯します。 だから、最初にそれを確認してください! それ以外の場合は、それは動作しませんし、間違った答えを取得します。 L’hopitalのルールを使用するためのガイドは次のとおりです。
- ステップ1:制限を直接評価します。
- ステップ2:不確定な形式のいずれかであるかどうかを確認します。 そうであれば、ステップ3に進みます。,
- ステップ3:l’hopitalのルールを使用します。
- ステップ4:別の不確定なフォームが得られるかどうかを確認します。 そうした場合は、手順3を繰り返します。
これらの手順を使用していくつかの例を見てみましょう。
質問6:限界を評価します
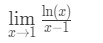
- ステップ1:制限を直接評価すると、
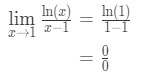
式9:L’hopitalのルール質問pt。,2 - ステップ2:
はい、これは不確定な形式の一つです。
- ステップ3:
l’hopitalのルールを適用すると、次のようになります。
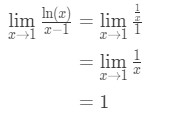
式9:L’hopitalのルール質問pt。3 - ステップ4:
一つは不確定な形式ではないので、完了し、答えは1です。
この質問は少し簡単でしたので、少し難しいものを見てみませんか。,
質問7:限界を評価します
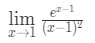
- ステップ1:制限を直接評価すると、
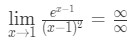
式10:L’hopitalのルールは二度質問pt。2 - ステップ2:
これは不確定な形式なので、ステップ3に進みます。,
- ステップ3:
l’hopitalのルールを適用すると、
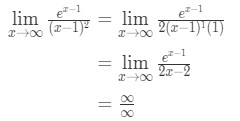
式10:L’hopitalのルールは二度質問pt。3 - ステップ4:
これは別の不確定な形式です。 したがって、ステップ3に戻り、l’hoptialのルールを再度適用する必要があります。
- ステップ3:
l’hopitalのルールを再び適用すると、
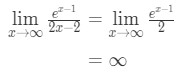
式10:L’hopitalのルールは二度質問pt。,4 - ステップ4:
無限大は不確定な形式ではないので、完了し、答えは∞\infty∞