Supponiamo di voler considerare l’impatto di un fattore di rischio sul tempo al verificarsi di un evento. Ad esempio, Arnlov et al (2010) considerano l’impatto dell’indice di massa corporea (BMI) e della sindrome metabolica sullo sviluppo di malattie cardiovascolari e morte negli uomini di mezza età. Le associazioni sono state studiate utilizzando i dati di uno studio di coorte di 1758 uomini svedesi di mezza età residenti in una contea con oltre 30 anni di follow-up., La figura seguente descrive il tempo di un evento cardiovascolare importante per categoria BMI e presenza (B) o assenza (A) di sindrome metabolica. C’è una differenza in queste curve di sopravvivenza?

Figura 2: Curve di Kaplan-Meier per i principali eventi cardiovascolari in diverse categorie di BMI in individui senza MetS (A) e con MetS (B).

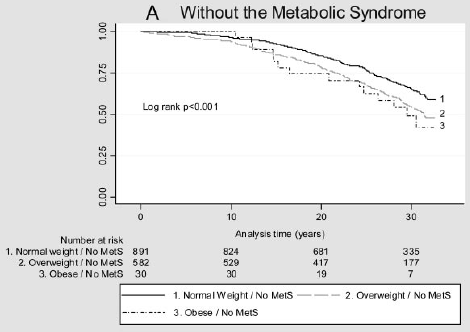
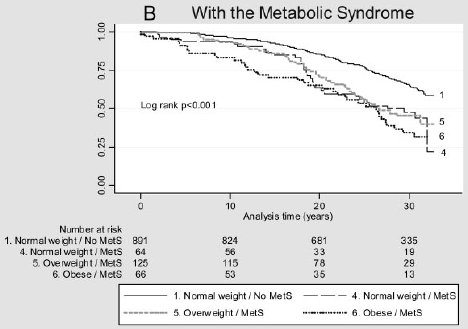
(Figure riprodotte da Arnlov, J et al., Impatto dell’indice di massa corporea e della sindrome metabolica sul rischio di malattie cardiovascolari e morte negli uomini di mezza età. Circolazione 2010; 121; 230-236, originariamente pubblicato on-line 12/28/2009; DOI 10.1161/CIRCULATIONAHA.109.88752)

Il verificarsi di un evento cardiovascolare maggiore è una risposta binaria. La regressione logistica, con BMI come variabile predittiva, sarebbe appropriata per analizzare questi dati?,

Risposta

La relazione tra la presenza o l’assenza di un evento cardiovascolare importante e la variabile predittiva potrebbe essere valutata con regressione logistica in un determinato momento, ma questo non confronterebbe direttamente le curve di sopravvivenza. Un’analisi di sopravvivenza confronterebbe le curve sulla base del tempo con l’evento.

I metodi di analisi della sopravvivenza, come la regressione dei pericoli proporzionali, differiscono dalla regressione logistica valutando un tasso anziché una proporzione.,

Regressione dei pericoli proporzionali Chiamata anche regressione di Cox, modella l’incidenza o il tasso di pericolo, il numero di nuovi casi di malattia per popolazione a rischio per unità di tempo. Se il risultato è la morte, questo è il tasso di mortalità.
Funzione di pericolo La funzione di pericolo è la probabilità che se una persona sopravvive a t, sperimenterà l’evento nel prossimo istante.

Regressione logistica al contrario, considera la percentuale di nuovi casi che si sviluppano in un dato periodo di tempo, cioè l’incidenza cumulativa., La regressione logistica stima l’odds ratio; la regressione proporzionale dei pericoli stima l’hazard ratio.

Il rapporto tra le funzioni di pericolo può essere considerato un rapporto tra le funzioni di rischio, quindi il modello di regressione proporzionale dei pericoli può essere considerato come funzione del rischio relativo (mentre i modelli di regressione logistica sono una funzione di un odds ratio). Le variazioni di una covariata hanno un effetto moltiplicativo sul rischio basale. Il modello in termini di funzione di pericolo al tempo t è:

\(\lambda \ left (t / X_{1i}, X_{2i},…,X_{Ki} \right )=\lambda_ {0} (t)exp \ left (\beta_{1}X_{1i}+ \ beta_{2} X_{2i}+…,+ \beta_{K}X_{Ki} \right)\)

Sebbene non sia selezionato un particolare modello di probabilità per rappresentare i tempi di sopravvivenza, la regressione dei pericoli proporzionali ha un presupposto importante: il pericolo per ogni individuo è una proporzione fissa del pericolo per qualsiasi altro individuo. (cioè, rischi proporzionali)., Avviso se \(\lambda_0 (t)\) è la funzione di rischio per un soggetto con tutte le predittore i valori pari a zero e \(\lambda_1 (t)\) è la funzione di rischio per un soggetto con altri valori per le variabili predittive, quindi il rapporto di rischio dipende solo da variabili predittive e non sul tempo t. Questa ipotesi significa che se una covariata raddoppia il rischio di un evento al giorno, si raddoppia anche il rischio dell’evento in qualsiasi altro giorno.,

I modelli di pericoli proporzionali possono essere utilizzati per misure discrete o continue del tempo degli eventi e possono incorporare covariate dipendenti dal tempo (covariate i cui valori possono cambiare durante il periodo di osservazione). Utilizzando la regressione proporzionale dei pericoli, è possibile produrre rapporti di pericolo (o rischio) regolati dalla covariata.

Torniamo alla domanda originale posta da Arnlov e colleagues…do BMI e sindrome metabolica influenzano lo sviluppo di malattie cardiovascolari? Leggi il Arnlov et al., Impatto dell’indice di massa corporea e della sindrome metabolica sul rischio di malattie cardiovascolari e morte negli uomini di mezza età Circolazione 2010; 121; 230-236, con particolare attenzione ai metodi statistici, ai risultati e alle conclusioni.

Confronta e contrasta l’approccio proporzionale di regressione dei rischi con un approccio di regressione logistica leggendo Franco et al. Traiettorie di entrare nella sindrome metabolica: Il Framingham Heart Study. Circolazione 2009; 120; 1943-1950; originariamente pubblicato online 2 novembre 2009; American Heart Association. 7272 Greenville Viale, Dallas, TX DOI: 10.,1161 / CIRCULATIONAHA.109.855817

È inoltre possibile confrontare i risultati dei due studi. Entrambi i documenti sono nella cartella Letture per la settimana 14.

Nota! Se non si ha familiarità con le curve di Kaplan-Meier, leggere il capitolo Analisi di sopravvivenza nelle monografie Research Methods II dal Journal of Tropical Pediatrics

(accessibile da http://www.oxfordjournals.org/our_journals/tropej/online/ma_chap12.pdf )

0