Dopo il raggio e il diametro, un’altra parte importante di un cerchio è un arco. In questo articolo, discuteremo in dettaglio cos’è un arco, come trovare la lunghezza di un arco e la misurazione di una lunghezza dell’arco in radianti. Studieremo anche l’arco minore e l’arco maggiore.
Che cos’è un arco di un cerchio?
Un arco di un cerchio è qualsiasi porzione della circonferenza di un cerchio. Per ricordare, la circonferenza di un cerchio è il perimetro o la distanza attorno a un cerchio., Pertanto, possiamo dire che la circonferenza di un cerchio è l’arco completo del cerchio stesso.
Come trovare la lunghezza di un arco?
La formula per calcolare l’arco afferma che:
lunghezza dell’Arco = 2nr (θ/360)
Dove r = raggio del cerchio,
π = pi = 3.14
q = angolo (in gradi) sotteso da un arco al centro del cerchio.
360 = l’angolo di una rotazione completa.
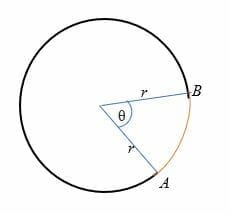
Dall’illustrazione precedente, la lunghezza dell’arco (disegnata in rosso) è la distanza dal punto A al punto B.,
Risolviamo alcuni problemi di esempio sulla lunghezza di un arco:
Esempio 1
Dato che arc AB sottende un angolo di 40 gradi al centro di un cerchio il cui raggio è di 7 cm. Calcola la lunghezza dell’arco AB.
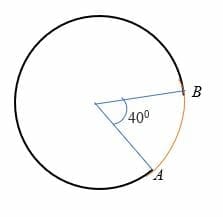
Soluzione
Dato r = 7 cm
θ = 40 gradi.
Per sostituzione,
La lunghezza di un arco = 2nr(θ/360)
Lunghezza = 2 x 3,14 x 7 x 40/360
= 4,884 cm.
Esempio 2
Trova la lunghezza di un arco di un cerchio che sottende un angolo di 120 gradi al centro di un cerchio il cui raggio è di 24 cm.,
Soluzione
La lunghezza di un arco = 2nr(θ/360)
= 2 x 3,14 x 24 x 120/360
= 50,24 cm.
Esempio 3
La lunghezza di un arco è di 35 m. Se il raggio del cerchio è di 14 m, trova l’angolo sotteso dall’arco.
Soluzione
La lunghezza di un arco = 2nr(θ/360)
35 m = 2 x 3,14 x 14 x (θ/360)
35 = 87,92 θ/360
Moltiplicare entrambi i lati per 360 per rimuovere la frazione.
12600 = 87,92 θ
Dividi entrambi i lati per 87,92
θ = 143,3 gradi.,
Esempio 4
Trova il raggio di un arco che è lungo 156 cm e sottende un angolo di 150 gradi al centro di un cerchio.
Soluzione
La lunghezza di un arco = 2nr(θ/360)
156 cm = 2 x 3,14 x r x 150/360
156 = 2,6167 r
Dividere entrambi i lati per 2,6167
r = 59,62 cm.
Quindi, il raggio dell’arco è 59,62 cm.
Come trovare la lunghezza dell’arco in radianti?
Esiste una relazione tra l’angolo sotteso da un arco in radianti e il rapporto tra la lunghezza dell’arco e il raggio del cerchio., In questo caso,
θ = (la lunghezza di un arco) / (il raggio del cerchio).
Pertanto, la lunghezza dell’arco in radianti è data da,
S = r θ
dove, θ = angolo sotteso da un arco in radianti
S = lunghezza dell’arco.
r = raggio del cerchio.
Un radiante è l’angolo centrale sotteso da una lunghezza d’arco di un raggio cioè s = r
Il radiante è solo un altro modo di misurare la dimensione di un angolo. Ad esempio, per convertire gli angoli da gradi a radianti, moltiplicare l’angolo (in gradi) per π/180.,
Allo stesso modo, per convertire i radianti in gradi, moltiplicare l’angolo (in radianti) per 180/π
Esempio 5
Trova la lunghezza di un arco il cui raggio è di 10 cm e l’angolo sotteso è di 0,349 radianti.
Soluzione
Lunghezza dell’arco = r θ
= 0,349 x 10
= 3,49 cm.
Esempio 6
Trova la lunghezza di un arco in radianti, che ha un raggio di 10 m e un angolo di 2,356 radianti.
Soluzione
Arc length = r θ
= 10 m x 2,356
= 23,56 m.
Esempio 7
Trova l’angolo sotteso da un arco che ha una lunghezza di 10,05 mm e un raggio di 8 mm.,
Soluzione
Lunghezza dell’arco = r θ
10.05 = 8 θ
Dividere entrambi i lati per 8.
1.2567 = θ
Lì, l’angolo sotteso dall’arco è 1.2567 radianti.
Esempio 8
Calcola il raggio di un cerchio la cui lunghezza dell’arco è di 144 metri e l’angolo dell’arco è di 3,665 radianti.
Soluzione
Lunghezza dell’arco = r θ
144 = 3,665 r
Dividere entrambi i lati per 3,665.
144/3.665 = r
r = 39.29 metri.
Esempio 9
Calcolare la lunghezza di un arco che sottende un angolo di 6.283 radianti al centro di un cerchio che ha un raggio di 28 cm.,
Soluzione
Lunghezza dell’arco = r θ
= 28 x 6,283
= 175,93 cm
Arco minore (h3)
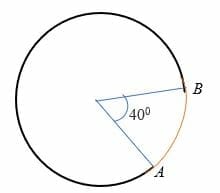
L’arco minore è un arco che sottende un angolo inferiore a 180 gradi rispetto al centro del cerchio. In altre parole, l’arco minore misura meno di un semicerchio ed è rappresentato sul cerchio da due punti. Ad esempio, arc AB nel cerchio sottostante è l’arco minore.
Arco maggiore (h3)
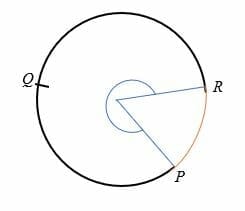
L’arco maggiore di un cerchio è un arco che sottende un angolo di oltre 180 gradi rispetto al centro del cerchio., L’arco maggiore è maggiore del semicerchio ed è rappresentato da tre punti su un cerchio.
Ad esempio, PQR è l’arco maggiore del cerchio mostrato di seguito.
Pratica Problemi
- Trovare l’area del settore di cerchio di raggio 9 mm. Assumere l’angolo sotteso da questo arco al centro è di 30 o.
- Città A Nord della città B. latitudini della città A e B sono 54 o N e 45 o N rispettivamente. Qual è la distanza Nord-Sud tra le due città? Il raggio della Terra è di 6400 km.,