nincs egyetlen stratégia fordítására matematikai kifejezéseket algebrai kifejezések. Mindaddig, amíg emlékszel az alapokra, képesnek kell lennie arra, hogy megbirkózzon a nagyobb kihívásokkal. Csak győződjön meg róla, hogy tudja igazolni, hogyan jön ki a saját algebrai kifejezés, és ami még fontosabb, hogy van értelme az Ön számára. Mindig kérjen segítséget a tanároktól, ha szükséges, vagy működjön együtt az osztálytársaival, hogy ellenőrizhesse válaszait.,
az algebrai kifejezések írásának készségeinek felépítéséhez különböző módokon megyünk át, hogy az egyes műveletek hogyan jelenhetnek meg szó vagy kifejezésként a problémában. Az érintett négy aritmetikai művelet összeadás, kivonás, szorzás és osztás.,
Key Words for Addition

Key Words for Subtraction

Key Words for Multiplication

Key Words for Division

It is time now time to go over some examples to practice writing algebraic expressions., A példákat két részre osztom:
- algebrai kifejezések alapvető példái
- többrészes példák algebrai kifejezésekre
alapvető algebrai kifejezések példák
1. példa: írjon egy algebrai kifejezést a “egy szám és négy összege”matematikai kifejezésre.
megoldás: az “összeg” szó azonnal megadja nekünk azt a tippet, amelyet itt fogunk hozzáadni. Vegye figyelembe, hogy két mennyiséget akarunk hozzáadni: egy ismeretlen számot és a 4-es számot. Mivel nem tudjuk, mi a szám értéke, használhatunk egy változót annak ábrázolására., Használhatja az ábécé bármely betűjét. Ebben az esetben beleegyezzünk abba, hogy y-t használjuk a változóhoz.
az y és a 4 változó hozzáadásakor y + 4 van. Az is rendben van, ha a választ 4 + y-ként írja, mert a kiegészítés kommutatív – vagyis a kiegészítés sorrendjének megváltoztatása nem változtatja meg annak összegét.
a végső válasz y + 4.
2. példa: írjon egy algebrai kifejezést a “10 számmal megnövelt” matematikai kifejezéshez.
megoldás: a “növelt” kulcsszavak kiegészítést jelentenek. Ez azt jelenti, hogy ismeretlen számot adtak hozzá a 10-hez., A K betű használatával változóként lefordíthatjuk a fenti állítást 10 + k-ként. mivel az összeadás kommutatív, átírhatjuk k + 10-ként. A fenti kettő közül bármelyik helyes válasz.
a végső válasz k + 10.
3. példa: írjon egy algebrai kifejezést az “1 és egy szám különbsége”matematikai kifejezésre.
megoldás: a “különbség” szó azt sugallja, hogy kivonjuk. Ezen túlmenően, ha találkozik ezzel a matematikai szóval (különbség), ügyeljen arra, hogy figyeljen a sorrendre. Az 1. szám az első, majd egy ismeretlen szám a második., Ez azt jelenti, hogy az 1-es szám a minuend, az ismeretlen szám pedig a subtrahend. Ha úgy döntünk, hogy az X betűt használjuk változóként, akkor a válasz 1 − x lesz.
a végső válasz 1 – x.
4.példa: írjon egy algebrai kifejezést a “8-nál kisebb szám”matematikai kifejezésre.
megoldás: legyen nagyon óvatos, ha foglalkozik a kulcsszavak “kevesebb, mint”. Az első mennyiség, amely a “kevesebb, mint” kulcsszavak előtt jön, amely “szám”, az altrahend. Míg a mennyiség, ami után jön, a minuend lesz.,
más szóval, kivonjuk az ismeretlen számot a 8-as számból. Ha úgy döntünk, hogy változónk az a betű, akkor 8 − a-t kapunk.
a végső válasz 8-A.
5. példa: írjunk egy algebrai kifejezést az “5 és egy szám szorzata”matematikai kifejezésre.
megoldás: két mennyiség vagy érték termékének megtalálásához azt jelenti, hogy együtt szaporítjuk őket. Ha az m betűt választjuk változónként, ennek a matematikai kifejezésnek az algebrai kifejezése egyszerűen 5m. ez azt jelenti, hogy az ismeretlen szám 5-szerese m.
a végső válasz 5m.,
6. példa: írjon egy algebrai kifejezést a “szám kétszerese”matematikai kifejezéshez.
megoldás: a “kétszer” szó azt jelenti, hogy megduplázunk valamit. Ebben az esetben meg akarjuk duplázni egy ismeretlen értéket vagy mennyiséget. Hagyja, hogy a D betű legyen az ismeretlen szám, amikor megduplázzuk, megkapjuk a 2D algebrai kifejezést.
a végső válasz 2D.
7. példa: írjon egy algebrai kifejezést a “szám hányadosa és 7″matematikai kifejezésre.
megoldás: a “hányados” kulcsszó azt jelenti, hogy az Osztás működését végezzük. Egy ismeretlen számot 7-tel osztunk meg., A W betű kiválasztása változóként, a fenti matematikai kifejezés az alábbi algebrai kifejezéssel fejezhető ki.
\LARGE{w \ over 7}
8. példa: írj egy algebrai kifejezést a “10-es és egy szám aránya”matematikai kifejezéshez.
megoldás: Hasonlóképpen, az “arány” szó divíziót jelent. A rend itt nagyon fontos. Az első mennyiség a 10-es szám, a második pedig az ismeretlen szám. Ez azt jelenti, hogy a 10-et egy ismeretlen szám osztja el., Legyen C az ismeretlen szám, a fenti matematikai kifejezés algebrai kifejezése
\LARGE{10 \ over c}
többrészes algebrai kifejezések példák
ezúttal olyan matematikai kifejezésekkel foglalkozunk, amelyek egy kicsit összetettebbek. Az algebrai kifejezések itt két vagy több műveletet tartalmazhatnak. Az alapvető kulcsszavak, hogy megtanuljuk, mielőtt szolgál majd az alapja, ahogy dolgozunk a nagyobb kihívást matematikai kifejezéseket értelmezni algebrai kifejezések.,
1.példa: írjon egy algebrai kifejezést a”szám több mint kétszerese” matematikai kifejezéshez.
megoldás: annak érdekében, hogy ezt sokkal könnyebben megértsük, ezt a kifejezést két részre osztjuk. Először ismerd fel, hogy ismeretlen számunk van. Az ábécé bármely betűjével képviselhetjük. Hagyja, hogy az ismeretlen szám legyen az X változó. az alábbi ábra segít nekünk megnézni, mi történik valójában.,
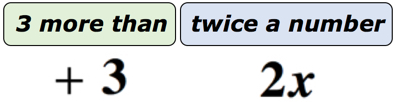
ha belegondolunk, van egy ismeretlen szám, amelyet x változó képvisel, amelyet megdupláznak vagy megszoroznak 2-vel. Bármi legyen is a termék, 3-at adunk hozzá. Tehát a végső válaszunknak úgy kell kinéznie, mint az alábbiakban.
a végső válasz 2x + 3.
2. példa: írjon egy algebrai kifejezést a “félszám és 10 különbsége”matematikai kifejezésre.
megoldás: tegyük fel, hogy az y változó az ismeretlen szám., A “különbség” kulcsszó arra készteti minket, hogy kivonást fogunk végrehajtani. Itt elengedhetetlen, hogy figyeljünk a kivonás sorrendjére. A “különbség” szó után két mennyiséget kell várnunk. Az első lesz a minuend, míg a második lesz a subtrahend. Vessen egy pillantást az alábbi ábrára.
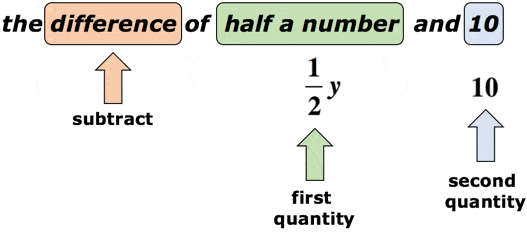
a fenti ábrára hivatkozva kivonjuk az első mennyiséget a második mennyiségből. Más szavakkal, a második mennyiséget levonják az első mennyiségből., A matematikai kifejezés végső válaszának ehhez hasonlónak kell lennie,
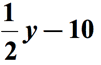
3 példa: írjon egy algebrai kifejezést a “7 kevesebb, mint egy szám és 6” matematikai kifejezéshez.
megoldás: tudjuk, hogy a” kevesebb, mint ” kivonási műveletet javasol. De itt egy kicsit óvatosnak kell lennünk, mert a kivonás sorrendje fontos. Tegyük fel, hogy az ismeretlen számot a K változó képviseli.,
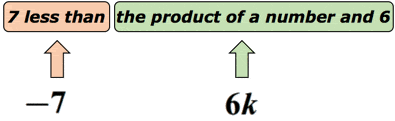
valójában ez a matematikai kifejezés átírható:
” a szám és a 6 mínusz 7 “
a “7 kevesebb, mint” jelentése “mínusz 7” a leírt mennyiségre, amely ebben az esetben “egy szám és 6”. Itt van a matematikai kifejezés végső értelmezése egy algebrai kifejezésben:
6K-7
4. példa: írjon egy algebrai kifejezést a “szám átlaga és 4” matematikai kifejezésre.,
megoldás: az adott matematikai kifejezés megkezdéséhez felül kell vizsgálnunk, hogy mit jelent az “átlag” szó. Két vagy több szám átlagának vagy átlagának kiszámításához össze kell adnunk az összes számot, hogy megkapjuk az összeget, majd osztjuk meg a bejegyzések számával vagy hány szám van. Ha hagyjuk, hogy m legyen az ismeretlen szám ábrázolására szolgáló változó, akkor a fenti matematikai kifejezés algebrai kifejezésekben fejezhető ki:
\LARGE{{m + 4} \over 2}
5 példa: írjon egy algebrai kifejezést az “1 hányadosa, 1 pedig egy számmal csökkent”matematikai kifejezésre.,
megoldás: a “hányados” kulcsszó azt jelenti, hogy megosztjuk. Ebben az esetben meg akarjuk osztani az 1-es számot az 1-es számmal csökkentett mennyiséggel. Az alábbiakban az algebrai kifejezés látható, amely a fenti matematikai kifejezést képviseli. Legyen egy az ismeretlen szám.
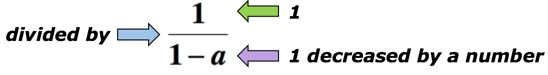
6.példa: írjon egy algebrai kifejezést a”egy szám négyzetének egyharmada, 2-vel növelve” matematikai kifejezésre.
megoldás: van néhány dolog folyik itt., Először is, a kifejezés azon része, amely “egy szám négyzetének egyharmadát” állítja, úgy értelmezhető,mint “egy szám négyzete osztva 3-mal”. Meg kell emelni az ismeretlen számot 2-vel, majd osztani 3-mal. Tegyük fel, hogy az ismeretlen szám t, kapunk
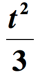
még nem végeztünk. Az utolsó lépés az, hogy a fenti mennyiséget 2-vel hozzáadjuk a ” 2-vel megnövelt “kifejezés fennmaradó részének beillesztéséhez. Tehát itt van az adott matematikai kifejezés végső ábrázolása.,
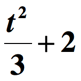
You might also be interested in:
Algebraic Expressions
Algebraic Sentences Word Problems