supposons que vous souhaitiez tenir compte de l’impact d’un facteur de risque sur le temps précédant la survenance d’un événement. Par exemple, Arnlov et al (2010) considèrent l’impact de l’indice de masse corporelle (IMC) et du syndrome métabolique sur le développement des maladies cardiovasculaires et de la mort chez les hommes d’âge moyen. Les associations ont été étudiées à l’aide des données d’une étude de cohorte de 1758 hommes suédois d’âge moyen résidant dans un comté avec plus de 30 ans de suivi., La figure ci-dessous représente le temps avant un événement cardiovasculaire majeur par catégorie D’IMC et la présence (B) ou l’absence (a) du syndrome métabolique. Est-il une différence dans ces courbes de survie?
Figure 2: courbes de Kaplan-Meier pour les événements cardiovasculaires majeurs dans différentes catégories D’IMC chez les individus sans MetS (A) et avec MetS (B).
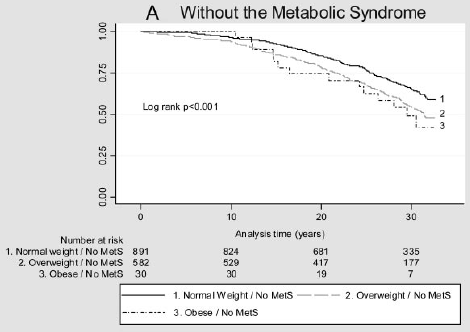
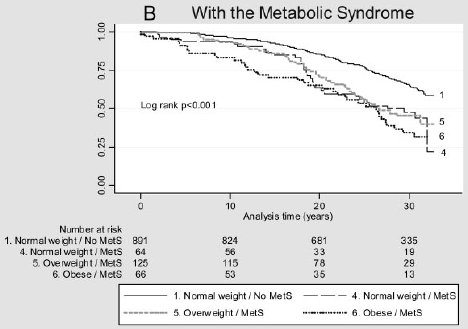
(Figures reproduites à partir de Arnlov, J et coll., Impact de L’indice de masse corporelle et du Syndrome métabolique sur le risque de maladie cardiovasculaire et de décès chez les hommes D’âge moyen. Circulation 2010; 121; 230-236, initialement publié en ligne 12/28/2009; DOI 10.1161/CIRCULATIONAHA.109.88752)
La survenue d’un événement cardiovasculaire majeur est une réponse binaire. La régression logistique, avec L’IMC comme variable prédictive, serait-elle appropriée pour analyser ces données?,
réponse
la relation entre la présence ou l’absence d’un événement cardiovasculaire majeur et la variable prédictive pourrait être évaluée par régression logistique à un moment donné, mais cela ne comparerait pas directement les courbes de survie. Une analyse de survie comparerait les courbes sur la base du temps à l’événement.
Les méthodes d’analyse de la survie, comme la régression proportionnelle des risques, diffèrent de la régression logistique en évaluant un taux plutôt qu’une proportion.,
en revanche, la régression logistique tient compte de la proportion de nouveaux cas qui se développent au cours d’une période donnée, c’est-à-dire de l’incidence cumulative., La régression logistique estime le rapport de cotes; la régression proportionnelle des risques estime le rapport de risques.
Le rapport des fonctions de risque peut être considéré comme un rapport des fonctions de risque, de sorte que le modèle de régression des risques proportionnels peut être considéré comme une fonction du risque relatif (alors que les modèles de régression logistique sont une fonction d’un rapport de cotes). Les changements dans une covariable ont un effet multiplicatif sur le risque de référence. Le modèle en termes de la fonction de risque à l’instant t est:
\(\lambda \left ( t|X_{1i},X_{2i},…,X_{Ki} \right )=\lambda_{0} (t)exp\left ( \beta_{1}X_{1i}+\beta_{2}X_{2i}+…,+ \ beta_{K} X_ {Ki} \ right)\)
bien qu’aucun modèle de probabilité particulier ne soit choisi pour représenter les temps de survie, la régression proportionnelle des dangers comporte une hypothèse importante: le danger pour tout individu est une proportion fixe du danger pour tout autre individu. (c.-à-d. risques proportionnels)., Remarque Si \(\lambda_0 (t)\) est la fonction de danger pour un sujet avec toutes les valeurs de prédicteur égales à zéro et \(\lambda_1 (t)\) est la fonction de danger pour un sujet avec d’autres valeurs pour les variables de prédicteur, alors le rapport de danger dépend uniquement des variables de prédicteur et non de l’heure T. Cette hypothèse signifie que si une covariable double le risque de l’événement le premier jour, elle double également le risque de l’événement n’importe quel autre jour. ,
Les modèles de risques proportionnels peuvent être utilisés pour des mesures discrètes ou continues du temps des événements et peuvent incorporer des covariables dépendant du temps (covariables dont les valeurs peuvent changer pendant la période d’observation). En utilisant la régression proportionnelle des dangers, des ratios de danger (ou de risque) ajustés par covariables peuvent être produits.
revenons à la question originale posée par Arnlov et colleagues…do L’IMC et le syndrome métabolique affectent le développement des maladies cardiovasculaires? Lire le Arnlov et al., Impact de L’indice de masse corporelle et du Syndrome métabolique sur le risque de maladie cardiovasculaire et de décès chez les hommes D’âge moyen Circulation 2010;121;230-236, en accordant une attention particulière aux méthodes statistiques, aux résultats et aux conclusions.
comparer et comparer L’approche de régression proportionnelle des risques à une approche de régression logistique en lisant Franco et al. Trajectoires d’entrée dans le Syndrome métabolique: L’étude cardiaque de Framingham. Circulation 2009;120; 1943-1950; initialement publié en ligne Nov 2, 2009; American Heart Association. 7272 Greenville Avenue, Dallas, TX DOI: 10.,1161 / CIRCULATIONAHA.109.855817
Vous pouvez également comparer les résultats des deux études. Les deux articles sont dans le dossier Lectures pour la Semaine 14.
(accessible depuis http://www.oxfordjournals.org/our_journals/tropej/online/ma_chap12.pdf)