Après le rayon et le diamètre, une autre partie importante d’un cercle est un arc. Dans cet article, nous discuterons en détail de ce qu’est un arc, comment trouver la longueur d’un arc et la mesure d’une longueur d’arc en radians. Nous étudierons également l’arc mineur et l’arc majeur.
qu’est-ce qu’un Arc de cercle?
un arc de cercle est de toute partie de la circonférence d’un cercle. Pour rappel, la circonférence d’un cercle est le périmètre ou la distance autour d’un cercle., Par conséquent, nous pouvons dire que la circonférence d’un cercle est l’arc complet du cercle lui-même.
Comment Trouver la Longueur d’un Arc?
La formule pour calculer l’arc stipule que:
longueur de l’Arc = 2nr (θ/360)
Où r = le rayon du cercle,
π = pi = 3.14
θ = l’angle (en degrés) sous-tendues par un arc de cercle au centre du cercle.
360 = l’angle d’une rotation complète.
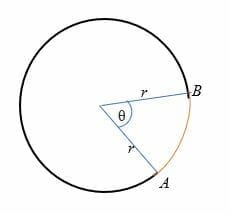
D’après l’illustration ci-dessus, la longueur de l’arc (dessinée en rouge) est la distance entre le point A et le point B.,
examinons quelques exemples de problèmes sur la longueur d’un arc:
exemple 1
étant donné que l’arc AB sous-tend un angle de 40 degrés par rapport au centre d’un cercle dont le rayon est de 7 cm. Calculez la longueur de l’arc AB.
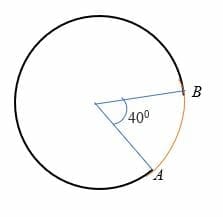
la Solution
etant Donné r = 7 cm
θ = 40 degrés.
Par substitution,
La longueur d’un arc = 2nr(θ/360)
Longueur = 2 x 3,14 x 7 x 40/360
= 4.884 cm.
Exemple 2
Trouver la longueur d’un arc de cercle qui sous-tend un angle de 120 degrés pour le centre d’un cercle dont le rayon est de 24 cm.,
la Solution
La longueur d’un arc = 2nr(θ/360)
= 2 x 3,14 x 24 x 120/360
= 50.24 cm.
Exemple 3
La longueur d’un arc est de 35 mètres. Si le rayon du cercle est de 14 m, trouver l’angle sous-tendu par l’arc.
la Solution
La longueur d’un arc = 2nr(θ/360)
35 m = 2 x 3,14 x 14 x (θ/360)
35 = 87.92 θ/360
Multiplier les deux côtés par 360 pour supprimer la fraction.
12600 = 87.92 θ
Diviser les deux côtés par 87.92
θ = 143.3 degrés.,
exemple 4
trouvez le rayon d’un arc de 156 cm de longueur et sous-tend un angle de 150 degrés par rapport au centre d’un cercle.
la Solution
La longueur d’un arc = 2nr(θ/360)
156 cm = 2 x 3,14 x r x 150/360
156 = 2.6167 r
Diviser les deux côtés par 2.6167
r = 59.62 cm.
ainsi, le rayon de l’arc est de 59,62 cm.
Comment trouver la longueur de L’Arc en Radians?
il existe une relation entre l’angle sous-tendu par un arc en radians et le rapport de la longueur de l’arc au rayon du cercle., Dans ce cas,
θ = (la longueur d’un arc) / (le rayon du cercle).
par conséquent, la longueur de l’arc en radians est donnée par,
S = r θ
où, θ = angle sous-tendu par un arc en radians
S = longueur de l’arc.
r = rayon du cercle.
Un radian est le centre de l’angle sous-tendu par une longueur d’un arc d’un rayon c’est à dire s = r
Le radian est juste une autre façon de mesurer la taille d’un angle. Par exemple, pour convertir les angles de degrés en radians, multipliez l’angle (en degrés) par π/180.,
de même, pour convertir les radians en degrés, multipliez l’angle (en radians) par 180/π
exemple 5
trouvez la longueur d’un arc dont le rayon est de 10 cm et l’angle sous-tendu est de 0,349 radians.
la Solution
longueur de l’Arc = r θ
= 0.349 x 10
= 3.49 cm.
Exemple 6
Trouver la longueur d’un arc en radians, qui a un rayon de 10 m et un angle de 2.356 radians.
la Solution
longueur de l’Arc = r θ
= 10 m x 2.356
= 23.56 m.
Exemple 7
Trouver l’angle sous-tendu par un arc qui a une longueur 10,05 mm et un rayon de 8 mm.,
la Solution
longueur de l’Arc = r θ
10.05 = 8 θ
Diviser les deux côtés par 8.
1.2567 = θ
Il y, l’angle sous-tendu par l’arc est 1.2567 radians.
exemple 8
calculer le rayon d’un cercle dont la longueur d’arc est de 144 yards et l’angle d’arc, est de 3,665 radians.
la Solution
longueur de l’Arc = r θ
144 = 3.665 r
Diviser les deux côtés par 3.665.
144/3.665 = r
r = 39.29 mètres.
Exemple 9
Calculer la longueur d’un arc qui sous-tend un angle de 6.283 radians au centre d’un cercle qui a un rayon de 28 cm.,
la Solution
longueur de l’Arc = r θ
= 28 x 6.283
= 175.93 cm
Mineure arc (h3)
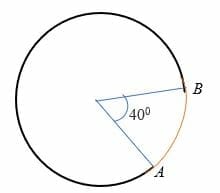
Le mineur à l’arc est un arc qui sous-tend un angle de moins de 180 degrés vers le centre du cercle. En d’autres termes, l’arc mineur mesure moins d’un demi-cercle et est représenté sur le cercle par deux points. Par exemple, l’arc AB dans le cercle ci-dessous est l’arc mineur.
grand arc (h3)
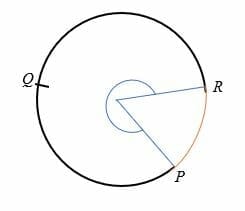
Le grand arc d’un cercle est un arc qui sous-tend un angle de plus de 180 degrés vers le centre du cercle., L’arc majeur est plus grand que le demi-cercle et est représenté par trois points sur un cercle.
par exemple, PQR est l’arc majeur du cercle illustré ci-dessous.
problèmes de pratique
- trouvez l’aire du secteur du cercle de rayon 9 mm. supposons que l’angle sous-tendu par cet arc au centre soit de 30 O.
- La Ville A est au nord de la ville B. Les latitudes de la ville A et de la ville B sont respectivement de 54 O N et de 45 o n. Quelle est la distance Nord-Sud entre les deux villes? Le rayon de la Terre est de 6400 km.,