Lineær Tilnærmelse
Lad os sige, at én dag du har glemt en lommeregner, og du virkelig ønsker at finde ud af, hvordan, hvad kvadratroden af 2 er. Hvordan ville vi finde ud af uden en lommeregner? Vi kan bruge lineær tilnærmelse!
linearisering af en funktion
lineariseringen af en funktion handler kun om at finde tangentlinjen for funktionen på et specifikt punkt på en anden måde., Den linearisering formel er:

hvor L(x) er ligningen for tangenten i et punkt.
Hvordan er det nyttigt for os? Nå, vi kan faktisk bruge denne ligning til at tilnærme værdier af funktionen nær punkt A. se på denne graf.,
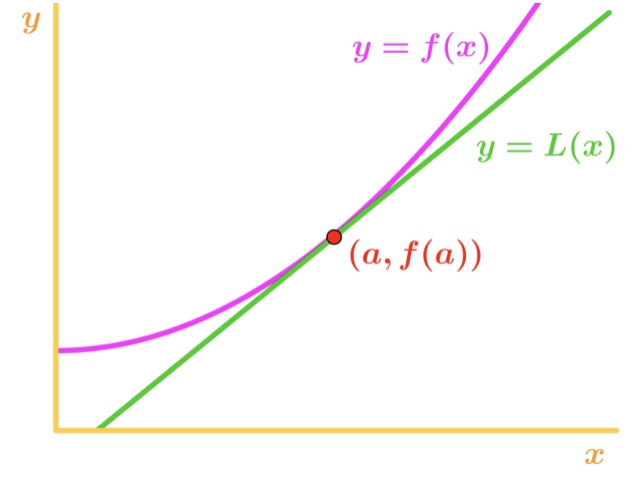
Bemærk, at for x-værdier i nærheden af punkt a, kan vi se, at funktion og tangenten er relativt tæt på hinanden. På grund af dette er vi i stand til at skrive, at funktionen er omtrent lig med tangentlinjen nær punkt A., Med andre ord,

hvor ≈\ca≈ er ca symbol. Denne ligning er kendt som den lineære tilnærmelse formel. Det er lineært på en måde, at tangenten er en lige linje, og vi bruger den til at tilnærme funktionen. Ved hjælp af denne tilnærmelse er vi i stand til at tilnærme værdier, der ikke kan gøres manuelt. For eksempel kan kvadratroden af 2 eller den naturlige log på 5 alle tilnærmes!, En vigtig ting at bemærke er, at denne tilnærmelse kun virker for values-værdier nær punkt A. Hvis du har en value-Værdi langt fra punkt A, bliver tilnærmelsen virkelig unøjagtig.
nu tager vi ikke et kig på et par eksempler på at finde lineariseringen af en funktion og så se på, hvordan man bruger lineær tilnærmelse!
Find den linearisering af L(x) af funktionen i et
Spørgsmål 1: Anser den funktion
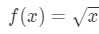
lad os sige, at vi vil finde lineariseringen af funktionen ved punkt A=4.
for At finde den linearisering L(x), minde om, at

- Trin 1: Find et
- Trin 2: Find f(a)
- Trin 3: Find f'(a). trin 4: Sæt alle tre i formlen for at finde L ())
-
lad os følge disse trin!,
Trin 1: heldigvis gives a = 4 til os i spørgsmålet, så vi behøver ikke at kigge efter det.
- Trin 2:
Bemærk at
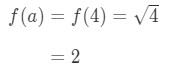
Ligning 1: Linearisering spørgsmål pt. 3 - Trin 3:
Vide, at den afledte af kvadratrødder er
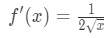
Ligning 1: Linearisering spørgsmål pt., 4 And so plugging in x=a gives us:
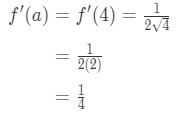
Equation 1: Linearization question pt. 5 - Step 4:
Since we know a, f(a), and f'(a), we can now plug it into L(x) to find the linearization of f(x).
Hence,
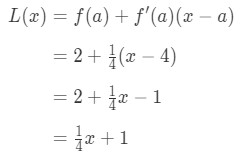
Equation 1: Linearization question pt., 6 Så L(x)=14\frac{1}{4}41x+1 linearisering af denne funktion ved punkt x=4. Derudover er det også tangentlinjen for funktionen ved punkt= = 4.
hvordan man gør lineær tilnærmelse
husk tidligere vi sagde, at vi kunne bruge ligningen af tangentlinjen til at tilnærme værdier for funktionen nær a? Lad os prøve dette med den linearisering, vi fandt tidligere. Husk på, at
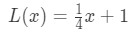
for punkter nær= = 4. Vi kan ændre dette til en lineær tilnærmelse til f(x) ved at sige at:
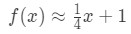
lad os nu sige, at jeg vil tilnærme f(4.04). Hvis du skulle tilslutte dette til den oprindelige funktion, så ville du få 4.04\s .rt{4.04}4.04 . Dette ville være virkelig svært at beregne uden en lommeregner., Men, ved hjælp af en lineær tilnærmelse, vi kan sige, at

nu har disse spørgsmål givet os en funktion og et punkt at arbejde med. Hvad hvis ingen af disse blev givet overhovedet? Hvad hvis spørgsmålet kun fortæller os at estimere et tal?
brug lineær tilnærmelse til at estimere et tal
Antag, at vi vil estimere 10\s .rt{10}10. Hvordan ville vi gøre det?, Vi skal bruge den lineære tilnærmelse

men vi har ikke engang en funktion og et punkt at arbejde med. Det betyder, at vi er nødt til at lave dem selv. Dette fører os til at gøre følgende:
- Trin 1: oprette en funktion
- Trin 2: opret et punkt
- Trin 3: Find f(a) og f'(a)
- Trin 4: Sæt alt ind i den lineære tilnærmelse formel
Lad os følge trinene!,spørgsmål 2: skøn 10\s .rt{10}10
- Trin 1: Lad os komme med en funktion. Bemærk, at vi estimering
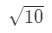
Ligning 3: Estimat med lineær ca. pt.2 vi skal på en eller anden måde skabe et forhold mellem f (() og 10\s .rt{10}10. Vi kan ikke sige, at f ( = ) = 10\s {rt{10}10 fordi funktionen ikke vil være afhængig af.. så hvorfor gør vi det ikke? Lad
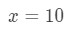
Ligning 3: Estimat med lineær ca. pt.,3 Hvis vi gør det, så er vi stort set at sige,
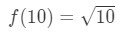
Ligning 3: Estimat med lineær ca. pt.4 vi kan nu selvfølgelig fortælle, hvad funktionen skal være. Lad
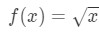
Ligning 3: Estimat med lineær ca. pt.5 så vi har en funktion, men nu har vi brug for et punkt A at arbejde med.,trin 2:
nøglen til at finde den rigtige værdi A er ved at overveje to ting:
1) Sørg for, at værdien A er tæt på
2) Sørg for, at f(A) er et dejligt tal.
Ville A = 8 være tilstrækkelig nok? Godt, 8 er temmelig tæt på 10, så det er ikke dårligt. Men,
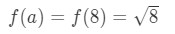
Ligning 3: Estimat med lineær ca. pt.6 Bemærk, at 8\s .rt{8}8 ikke er et meget flot nummer. Faktisk får du en masse decimaltal. Så vi er nødt til at prøve noget andet.,
Ville a = 9 være tilstrækkelig nok? Igen er 9 temmelig tæt på 10, så det er okay. Også,

Ligning 3: Estimat med lineær ca. pt.7 f(A) er faktisk et godt helt tal her, så det virker faktisk! Så at vælge a = 9 er tilstrækkeligt nok.
- Trin 3:
Bemærk, at der fra tidligere:

Ligning 3: Estimat med lineær ca. pt.,8 Calculating f'(x) we have again:

Equation 3: Estimate with linear approx. pt.9 So
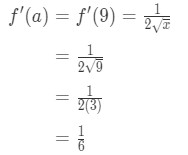
Equation 3: Estimate with linear approx. pt.,10 - Step 4:
Going back to the linear approximation formula we have:

Equation 3: Estimate with linear approx. pt.11 Plugging a, f(a), f'(a), f(x), and x in our formula you will see that:

Equation 3: Estimate with linear approx. pt.12 Hence, we just approximated the number!,
Hvis du vil have flere øvelsesproblemer om lineær tilnærmelse, anbefaler jeg, at du ser på dette link her.
http://tutorial.math.lamar.edu/Classes/CalcI/LinearApproximations.aspx
Overvurdere og Undervurdere
Vi ved, at lineære tilnærmelse er blot en vurdering af funktionens værdi på et bestemt punkt. Men hvordan ved vi, at hvis vores skøn er en overvurdering eller en undervurdering? Vi beregner det andet derivat og ser på konkaviteten.,
konkav op vs konkav ned
Hvis det andet derivat af funktionen er større end 0 for værdier nær A, er funktionen konkav op. Det betyder, at vores tilnærmelse vil være en undervurdering. Med andre ord,
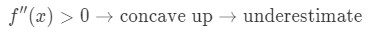
Formel 3: Undervurdere Hvorfor? Lad os se på denne graf.,
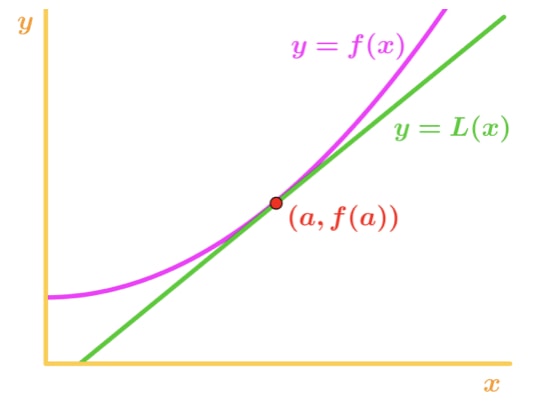
figur 2: Konkav op undervurdere Bemærk, at f(x) er konkav opad, og en tangent er en ret i henhold til f(x). Lad os sige var at bruge tangentlinjen til at tilnærme f (.). Derefter vil y-værdierne for tangentlinjen altid være mindre end den faktiske værdi af f (.). Derfor har vi en undervurdering
nu, hvis det andet derivat af funktionen er mindre end 0 for værdier nær A, så er funktionen konkav ned., Det betyder, at vores tilnærmelse vil være en overvurdering. Med andre ord,
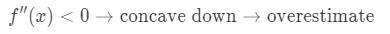
Formel 4: Overvurdere Igen, hvorfor? Lad os se på en anden graf.
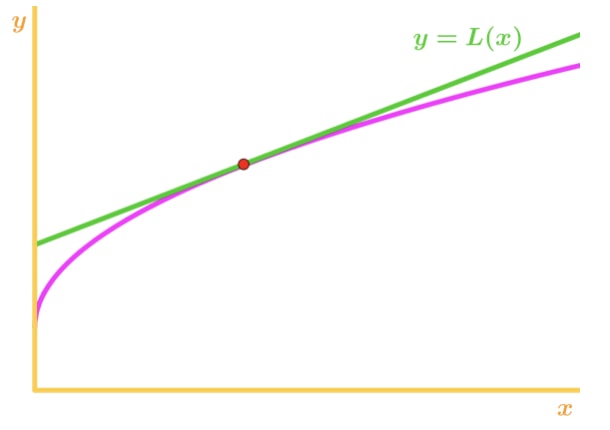
figur 3: Konkav ned overvurdere Bemærk, at f(x) er konkav nedad, og tangenten er lige over f(x). Igen, lad os sige, at vi vil bruge tangentlinjen til at tilnærme f (.)., Derefter vil y-værdierne for tangentlinjen altid være større end den faktiske værdi af f (.). Derfor har vi en overvurdering.
Så hvis du nogensinde har brug for at se, om din værdi er en undervurdering eller en overvurdering, sørg for at du følger disse trin:
- Trin 1: Find de anden afledte
- Trin 2: se på den hule af funktion nær et punkt
- Trin 3: Bekræfte, at det er en undervurdering/overvurdere
Lad os tage et kig på et eksempel:
Spørgsmål 3: Lad f(x) = x\sqrt{x}x og a = 4. Hvis vi lineære omtrentlige F (4.,04), ville det være en overvurdering eller en undervurdering?
- Trin 1: Se til, at
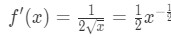
Ligning 4: Overvurdere spørgsmål pt.1 Så den anden afledte er
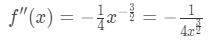
Ligning 4: Overvurdere spørgsmål pt.2 - Trin 2:
Bemærk at a=4, så vi vil se på positive værdier af.nær 4. Se nu på det andet derivat., Når x er positiv, vi kan se, at
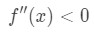
Ligning 4: Overvurdere spørgsmål pt.3 Derfor, det er konkav ned
- Trin 3:
Vi ved, at hvis funktion er konkav ned, så den tangent vil være over-funktion. Derfor vil brug af tangentlinjen som en tilnærmelse give en overvurderet værdi.
differentialer
ikke kun kan vi tilnærme værdier med lineær tilnærmelse, men vi kan også tilnærme med differentialer., At tilnærme vi bruge følgende formel
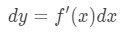
Formel 5: Forskelle hvor dy og dx er forskelle, og f'(x) er den afledede af f med hensyn til x. Da vi har at gøre med meget små ændringer i x og y, så vi kommer til at bruge det faktum at:
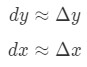
Ligning 5: Indbyrdes forskelle pt.,1 Men, de fleste af de spørgsmål, vi må inddrage indstilling
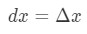
Ligning 5: Indbyrdes forskelle pt.2 Så ved hjælp af disse fakta vil føre os til at være:
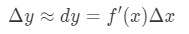
Ligning 5: Indbyrdes forskelle pt.3 denne tilnærmelse er meget nyttig, når tilnærmelsen af ændringen af y., Husk, at de ikke havde regnemaskiner, så dette er den bedste tilnærmelse, de kunne få til funktioner med firkantede rødder eller naturlige logfiler.
det meste af tiden bliver du nødt til at kigge efter F'(() og\ \ Delta.. selv. Med andre ord, skal du følge disse trin for at tilnærme\ \ Delta !y!
- Trin 1: Find\ \ Delta..
- Trin 2: Find f'(.)
- Trin 3: sæt alt i formlen for at finde dy. dy vil være tilnærmelse for\ \ Delta .y.
lad os se på et eksempel på at bruge denne tilnærmelse:
spørgsmål 4: Overvej funktionen y = ln (. + 1)., Antag changes ændringer fra 0 til 0,01. Omtrentlige\ \ Delta .y.
- Trin 1: Bemærk, at x ændres fra 0 til 0,01, så ændringen i x ville være:
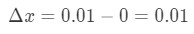
Ligning 6: Differential spørgsmål pt.1 - Trin 2:
Den afledte ville være:
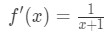
Ligning 6: Differential spørgsmål pt.,2 - Trin 3:
at Sætte alt, hvad i har vi:
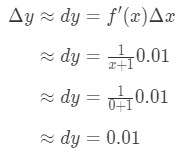
Ligning 6: Differential spørgsmål pt.3 Derfor, Δ\DeltaΔy ≈\ca≈ 0.01
Men, de fleste af den tid, vi ønsker at estimere en værdi af funktionen, og ikke ændringen af værdien. Dermed vil vi tilføje begge sider af ligningen med y, hvilket giver os:
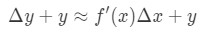
Ligning 6: Differential spørgsmål pt.,4 der er det samme som:
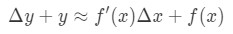
Ligning 6: Differential spørgsmål pt.5 denne ligning er lidt svært at læse, så vi vil omarrangere den endnu mere. Lad os prøve at slippe af med y og\ \ Delta .y. Bemærk, at Δ\DeltaΔy+ y er stort set det samme som at finde værdien af funktionen Δ\DeltaΔx+x. Med andre ord,
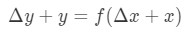
Ligning 6: Differential spørgsmål pt.,6 Derfor erstatte denne i vores tilnærmelse ovenfor, vil give os:
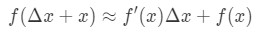
Ligning 6: Differential spørgsmål pt.7 hvor f (\\Delta..+.) er værdi, vi forsøger at estimere. Hvordan bruger vi denne formel? Jeg anbefaler at følge disse trin:
lad os bruge disse trin til følgende spørgsmål.spørgsmål 5: brug differentialer til at tilnærme 10\s {rt{10}10.
- Trin 1: Sammenlign f (\\Delta++++) med 10 \ s .rt{10}10., Since 10\sqrt{10}10 has a square root and 9 is a perfect square that is closest to 10, then let
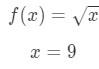
Equation 7: Approximate value with differentials pt.1 Notice that:
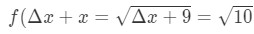
Equation 7: Approximate value with differentials pt.,2 Se, at der ikke er noget valg, men at lade Δ\DeltaΔx = 1
- Trin 2:
Se, at de afledte giver:

Ligning 7: Anslået værdi med forskelle pt.3 Så dette indebærer
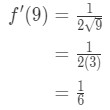
Ligning 7: Anslået værdi med forskelle pt.,4 - Trin 3:
at Sætte alt ind i formlen, får vi:
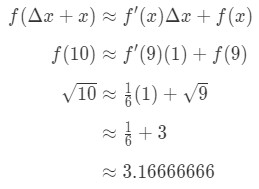
Ligning 7: Anslået værdi med forskelle pt.5 derfor tilnærmede vi bare antallet.
en interessant ting at bemærke er, at lineær tilnærmelse og forskelle begge giver det samme resultat for 10\s .rt{10}10.,
Hvis du ønsker at lære mere om forskelle, klik på dette link:
http://tutorial.math.lamar.edu/Classes/CalcI/LinearApproximations.aspx
Bevise L ‘hospital’ s Regel ved hjælp af en lineær tilnærmelse
Nu har vi lært en masse om lineære tilnærmelse, men hvad andet kan vi gøre med det? Vi kan faktisk bruge den lineære tilnærmelse formel til at bevise en regel kendt som L ‘Hospital’ s regel . Sådan fungerer beviset.
Huske, at den lineære tilnærmelse formel er:

Ligning 8: Følger l’hopital s regel pt.,1 Se, at vi kan flytte rundt på formlen, således at:
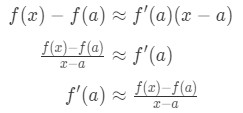
Ligning 8: Følger l’hopital s regel pt.2 indse, at tilnærmelsen bliver mere og mere præcis, når vi vælger values-værdier, der er tættere på A. med andre ord, hvis vi tager grænsen som.. A, vil de være ens. Så
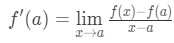
Ligning 8: Følger l’hopital s regel pt.,3 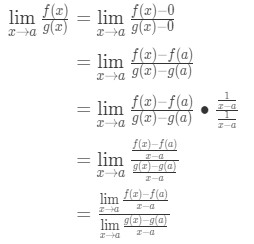
Ligning 8: Følger l’hopital s regel pt.4 Bemærk nu, at vi kan anvende den formel, vi har afledt tidligere lige her. Så nu
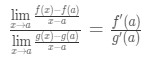
Ligning 8: Følger l’hopital s regel pt.5 Nu, i stedet for at skrive f'(a) og g'(a), kan vi anvende grænser som x→a (fordi vi ved, at f og g er differentiable)., Så
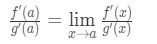
Ligning 8: Følger l’hopital s regel pt.6 Derfor, vi lige har vist at:
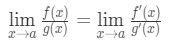
Formel 6: L’hopital s regel der er L ‘hospital’ s Regel .
Hvornår skal du bruge L ‘hopitals regel
Vi vil altid anvende l’ hoptials regel, når vi støder på ubestemte grænser. Der er to typer ubestemte former., Disse ubestemt former ville være:
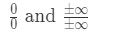
Formel 7: Ubegrænset former mange mennesker begår den fejl at bruge l’hopital er reglen uden selv at kontrollere, hvis det er en ubestemt grænse. Så sørg for at tjekke det først! Ellers fungerer det ikke, og du får det forkerte svar. Her er en vejledning til brug af L ‘ hopitals regel:
- Trin 1: Evaluer grænsen direkte.
- Trin 2: Kontroller, om det er en af de ubestemte former. Hvis det er, gå til trin 3.,
- Trin 3: Brug l ‘ hopitals regel.trin 4: Kontroller, om du får en anden ubestemt formular. Gentag trin 3, hvis du gør det.
lad os tage et kig på et par eksempler ved hjælp af disse trin.spørgsmål 6: Evaluer grænsen
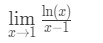
ligning 9: l ‘ hopitals regelspørgsmål pt.1 - Trin 1: Evaluering af den grænse, der direkte giver os
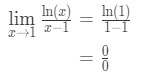
Ligning 9: L’hopital s regel spørgsmål pt.,2 - Trin 2:
Ja, det er en af de frie former.
- Trin 3:
Anvendelse af l’hopital ‘ s regel, vi har:
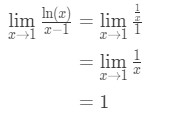
Ligning 9: L’hopital s regel spørgsmål pt.3 - Trin 4:
den ene er ikke et ubestemt form, så vi er gjort og svaret er 1.
nu var spørgsmålet lidt let, så hvorfor kigger vi ikke på noget, der er lidt sværere.,
Spørgsmål 7: Evaluere grænse
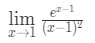
Ligning 10: L’hopital s regel to gange spørgsmål pt.1 - Trin 1: Evaluering af den grænse, der direkte ser vi, at:
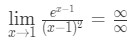
Ligning 10: L’hopital s regel to gange spørgsmål pt.2 - Trin 2:
Dette er et ubestemt form, så gå til trin 3.,
- Trin 3:
Anvendelse af l’hopital ‘ s regel, vi har
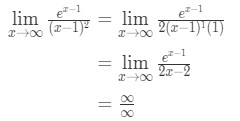
Ligning 10: L’hopital s regel to gange spørgsmål pt.3 - Trin 4:
Dette er en anden ubestemt form. Så vi er nødt til at gå tilbage til trin 3 og anvende l ‘hoptial’ s regler igen.
- Trin 3:
Anvendelse af l’hopital s regel igen har vi:
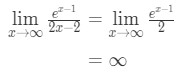
Ligning 10: L’hopital s regel to gange spørgsmål pt.,4 - Trin 4:
Infinity er ikke et ubestemt form, så vi er gjort og svaret er ∞\infty∞
- Trin 1: Lad os komme med en funktion. Bemærk, at vi estimering