Lineární Aproximace
řekněme, že jeden den jste zapomněli kalkulačku a opravdu chcete najít, jak to, co odmocnina z 2 je. Jak bychom to zjistili bez kalkulačky? Můžeme použít lineární aproximaci!
Linearizace funkce
linearizace funkce je jen o hledání tečny funkce v určitém bodě jiným způsobem., Linearizace vzorec je:

kde L(x) je rovnice tečny v bodě a.
Jak je to užitečné pro nás? Můžeme použít tuto rovnici k přiblížení hodnot funkce v blízkosti bodu a.podívejte se na tento graf.,
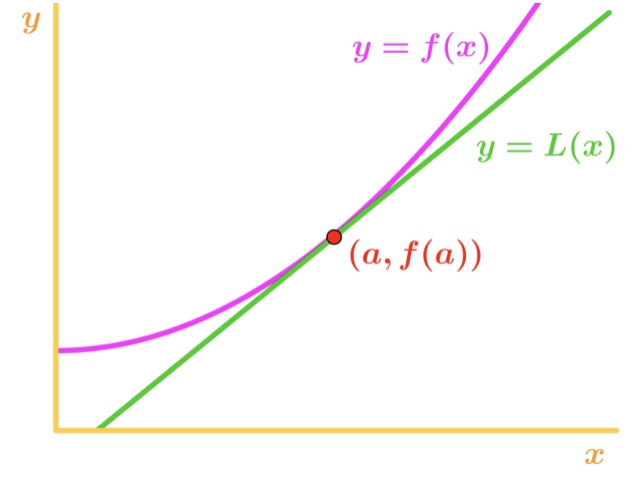
Všimněte si, že pro hodnoty x blízké bodu, vidíme, že funkce a tečny je relativně blízko sebe. Z tohoto důvodu jsme schopni napsat, že funkce je přibližně stejná jako tečna poblíž bodu a., Jinými slovy,

kde ≈\approx≈ je přibližně symbol. Tato rovnice je známá jako lineární aproximační vzorec. Je lineární v tom smyslu, že tečna je přímka a my ji používáme k přibližování funkce. Pomocí této aproximace jsme schopni přibližovat hodnoty, které nelze provést ručně. Například druhá odmocnina 2 nebo přirozený log 5 mohou být všechny aproximovány!, Jedna důležitá věc k poznámce je, že tato aproximace funguje pouze pro hodnoty x blízké bodu. Pokud budete mít x hodnotu daleko od bodu a, pak sbližování se stává opravdu nepřesné.
nyní se podíváme na několik příkladů nalezení linearizace funkce a pak se podíváme na to, jak používat lineární aproximaci!
Najít linearizace L(x) funkce
Otázka 1: Uvažujme funkci
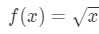
řekněme, že chceme najít linearizace funkce v bodě a=4.
najít linearizace L(x), připomeňme si, že

- Krok 1: Najít
- Krok 2: Najděte f(a)
- 3. Krok: Najděte f'(a).
- Krok 4: zapojte všechny tři do vzorce a najděte L (x)
-
pojďme postupovat podle těchto kroků!,
Krok 1: naštěstí je nám v otázce dána a = 4, takže ji nemusíme hledat.
- Krok 2:
Všimněte si, že
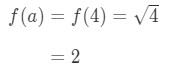
Rovnice 1: Linearizace otázku pt. 3 - Krok č. 3:
Víme, že derivace odmocniny,
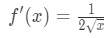
Rovnice 1: Linearizace otázku pt., 4 And so plugging in x=a gives us:
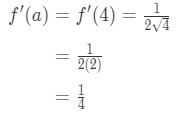
Equation 1: Linearization question pt. 5 - Step 4:
Since we know a, f(a), and f'(a), we can now plug it into L(x) to find the linearization of f(x).
Hence,
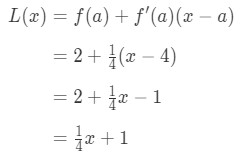
Equation 1: Linearization question pt., 6 L(x)=14\frac{1}{4}41x+1 je linearizace této funkce v bodě x=4. Kromě toho je to také tečna funkce v bodě x=4.
Jak to udělat lineární aproximace
Pamatujte, dříve jsme si řekli, že bychom mohli použít rovnici tečny k přibližné hodnoty funkce v blízkosti? Zkusme to s linearizací, kterou jsme našli dříve. Připomeňme, že
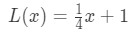
pro body poblíž x = 4. Můžeme změnit to do lineární aproximací pro f(x) tím, že:
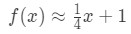
nyní řekněme, že chci přiblížit f (4.04). Pokud byste to měli připojit k původní funkci, získali byste 4.04\sqrt{4.04}4.04 . To by bylo opravdu těžké vypočítat bez kalkulačky., Nicméně, pomocí lineární aproximace, můžeme říci, že

nyní nám tyto otázky daly funkci a bod pro práci. Co když nic z toho nebylo dáno vůbec? Co když nám otázka pouze řekne, abychom odhadli číslo?
použijte lineární aproximaci pro odhad počtu
Předpokládejme, že chceme odhadnout 10 \ sqrt{10}10. Jak bychom to udělali?, Museli bychom použít lineární aproximaci

ale nemáme ani funkci a bod, se kterým bychom mohli pracovat. To znamená, že je musíme udělat sami. To nás vede k následující kroky:
- Krok 1: vytvoření funkce
- Krok 2: vytvořte bod a
- 3. Krok: Najděte f(a) a f'(a)
- Krok 4: Zapojte vše do lineární aproximace vzorec
postupujte podle pokynů!,
Otázka 2: odhad 10 \ sqrt{10}10
- Krok 1: pojďme přijít s funkcí. Všimněte si, že jsme odhad
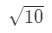
Rovnice 3: Odhad s lineárním cca. bod.2 potřebujeme se nějak vztah mezi f(x) a 10\sqrt{10}10. Nemůžeme říci, že f(x) = 10\sqrt{10}10 protože funkce nebude závislá na x. Tak proč to neděláme?
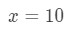
Rovnice 3: Odhad s lineárním cca. bod.,3 Pokud to uděláme, pak jsme v podstatě říká,
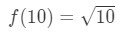
Rovnice 3: Odhad s lineárním cca. bod.4 nyní můžeme samozřejmě říci, jaká by měla být funkce.
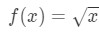
Rovnice 3: Odhad s lineárním cca. bod.5 takže máme funkci, ale nyní potřebujeme bod a pro práci s.,
- Krok 2:
klíčem k nalezení správné hodnoty, je s ohledem na dvě věci:
1) ujistěte Se, že hodnota je blízko k x
2) ujistěte Se, že f(a) je pěkné číslo.
stačilo by a = 8? No, 8 je docela blízko 10, takže to není špatné.
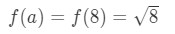
rovnice 3: odhad s lineární cca. bod.6 Všimněte si, že 8\sqrt{8}8 není moc pěkné číslo. Ve skutečnosti dostanete spoustu desetinných čísel. Takže musíme zkusit něco jiného.,
stačilo by a = 9? Opět platí, že 9 je docela blízko 10, takže je to v pořádku. Také,

Rovnice 3: Odhad s lineárním cca. bod.7 f(a) je vlastně pěkné celé číslo, takže to vlastně funguje! Takže výběr a=9 stačí.
- Krok č. 3:
Všimněte si, že z dříve:

Rovnice 3: Odhad s lineárním cca. bod.,8 Calculating f'(x) we have again:

Equation 3: Estimate with linear approx. pt.9 So
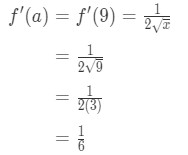
Equation 3: Estimate with linear approx. pt.,10 - Step 4:
Going back to the linear approximation formula we have:

Equation 3: Estimate with linear approx. pt.11 Plugging a, f(a), f'(a), f(x), and x in our formula you will see that:

Equation 3: Estimate with linear approx. pt.12 Hence, we just approximated the number!,
Pokud chcete více praktických problémů s lineární aproximací, doporučujeme vám podívat se na tento odkaz zde.
http://tutorial.math.lamar.edu/Classes/CalcI/LinearApproximations.aspx
Přeceňovat a Podceňovat
víme, že lineární aproximace je jen odhad funkční hodnotu v zadaném bodě. Jak však víme, že pokud je náš odhad nadhodnocený nebo podceňovaný? Vypočítáme druhý derivát a podíváme se na konkávitu.,
konkávní vs konkávní dolů
Pokud je druhá derivace funkce větší než 0 pro hodnoty poblíž a, pak je funkce konkávní nahoru. To znamená, že naše aproximace bude podceňována. Jinými slovy,
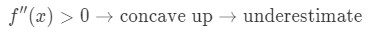
Proč? Podívejme se na tento graf.,
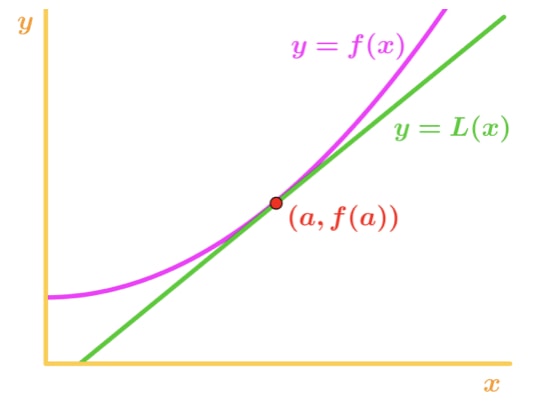
Všimněte si, že f(x) je konkávní směrem nahoru a tečna je pod f(x). Řekněme, že bylo použít tečnu k přibližné F (x). Pak hodnoty y tečny budou vždy menší než skutečná hodnota f(x). Proto máme podceňovat
Nyní, pokud je druhá derivace funkce menší než 0 pro hodnoty poblíž a, pak je funkce konkávní dolů., To znamená, že naše aproximace bude přeceňována. Jinými slovy,
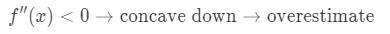
Opět, proč? Podívejme se na další graf.
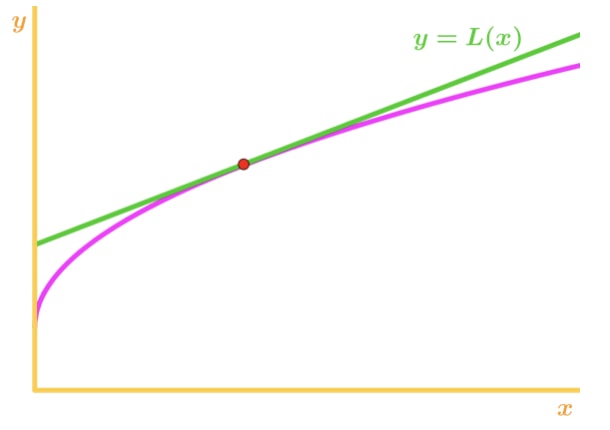
Všimněte si, že f(x) je konkávní směrem dolů a tečna je přímo nad f(x). Opět řekněme, že použijeme tečnu k přibližné F(x)., Pak hodnoty y tečny budou vždy větší než skutečná hodnota f(x). Proto máme nadhodnocení.
Takže, pokud budete někdy potřebovat zjistit, jestli vaše hodnota je podhodnocení nebo nadhodnocení, ujistěte se, že budete postupovat podle těchto kroků:
- Krok 1: Najděte druhou derivaci
- Krok 2: podívejte se na konkávnost funkce v blízkosti bodu a
- 3. Krok: Potvrdit, že to je podceňovat/přeceňovat
Pojďme se podívat na příklad:
Otázka 3: Nechť f(x) = x\sqrt{x}x, a = 4. Máme-li lineární přibližné f (4.,04), bylo by to přeceňování nebo podceňování?
- Krok 1: Vidět, že
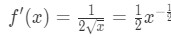
Rovnice 4: Přeceňovat otázku pt.1 Takže druhá derivace je
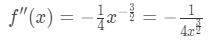
Rovnice 4: Přeceňovat otázku pt.2 - Krok 2:
Všimněte si, že a=4, takže chceme se podívat na pozitivní hodnoty x blízké 4. Nyní se podívejte na druhou derivaci., Když x je pozitivní, vidíme, že
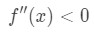
Rovnice 4: Přeceňovat otázku pt.3 Proto je konkávní
- Krok č. 3:
víme, že pokud je funkce konkávní, pak tečnu, bude výše uvedené funkce. Použití tečny jako aproximace proto poskytne nadhodnocenou hodnotu.
Rozdíly
nejen, můžeme přibližné hodnoty s lineární aproximací, ale můžeme se také sblížit s diferenciály., K přibližné, používáme následující vzorec,
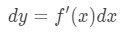
kde dy a dx jsou rozdíly, a f'(x) je derivace f za podmínky x. Protože máme co do činění s velmi malé změny v x a y, pak budeme používat fakt, že:
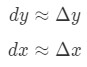
Nicméně, většina z otázek, které zahrnují nastavení,
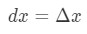
pomocí těchto skutečností nás povede k:
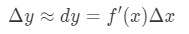
tato aproximace je velmi užitečná při aproximaci změny y., Mějte na paměti, že tehdy neměli kalkulačky, takže je to nejlepší přiblížení, které by mohli získat pro funkce se čtvercovými kořeny nebo přírodními protokoly.
většinu času budete muset hledat F'(x) a Δ\DeltaΔx sami. Jinými slovy, postupujte podle těchto kroků a přibližte Δ\DeltaΔy!
- Krok 1: Najít Δ\DeltaΔx
- Krok 2: Najděte f'(x)
- Krok 3: Zapojte vše do vzorce najít dy. dy bude aproximace pro Δ\DeltaΔy.
podívejme se na příklad použití této aproximace:
otázka 4: zvažte funkci y = ln (x + 1)., Předpokládejme, že X se změní z 0 na 0,01. Přibližná Δ\DeltaΔy.
- Krok 1: Všimněte si, že x se mění od 0 do 0,01, takže změna v x by byla:
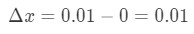
Rovnice 6: Diferenciální otázku pt.1 - Krok 2:
derivace by byla:
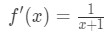
Rovnice 6: Diferenciální otázku pt.,2 - Krok č. 3:
Připojením všechno máme:
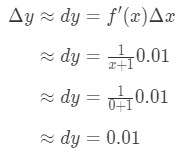
Rovnice 6: Diferenciální otázku pt.3 Proto, Δ\DeltaΔy ≈\approx≈ 0.01
Nicméně, většina z času, kolik chceme odhadnout hodnotu funkce a změna hodnoty. Proto přidáme na obou stranách rovnice podle y, které nám dává:
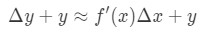
což je totéž jako:
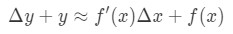
Tato rovnice je trochu těžké číst, a tak jsme se chystáte uspořádat ještě víc. Pokusíme se zbavit y a Δ\DeltaΔy. Všimněte si, že Δ\DeltaΔy+ y je v podstatě stejný jako zjištění, že hodnota funkce v Δ\DeltaΔx+x. Jinými slovy,
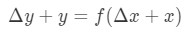
Proto, dosazením v naší sbližování výše bude nám:
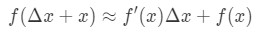
kde f(Δ\DeltaΔx+x) je hodnota snažíme odhadnout. Jak použijeme tento vzorec? Doporučuji postupovat podle těchto kroků:
použijeme tyto kroky pro následující otázku.
otázka 5: Použijte diferenciály k přiblížení 10 \ sqrt{10}10.
- Krok 1: Porovnejte f (Δ \ DeltaΔx + x) s 10 \ sqrt{10}10., Since 10\sqrt{10}10 has a square root and 9 is a perfect square that is closest to 10, then let
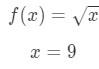
Equation 7: Approximate value with differentials pt.1 Notice that:
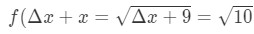
Equation 7: Approximate value with differentials pt.,2 je Vidět, že tam není žádný výběr ale nechat Δ\DeltaΔx = 1
- Krok 2:
je Vidět, že derivace dává:

Rovnice 7: Orientační hodnoty rozdílů pt.3 Takže to naznačuje,
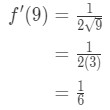
Rovnice 7: Orientační hodnoty rozdílů pt.,4 - Krok č. 3:
Zapojení vše do vzorce nám dává:
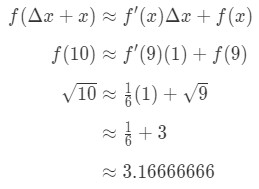
Rovnice 7: Orientační hodnoty rozdílů pt.5 proto jsme číslo jen přiblížili.
jedna zajímavá věc je, že lineární aproximace a diferenciály oba dávají stejný výsledek pro 10 \ sqrt{10}10.,
Pokud se chcete dozvědět více o diferenciály, klikněte na tento odkaz:
http://tutorial.math.lamar.edu/Classes/CalcI/LinearApproximations.aspx
Dokazuje, L’Hospital je Pravidlo, pomocí lineární aproximace
Nyní jsme se naučili hodně o lineární aproximaci, ale co jiného můžeme dělat? Ve skutečnosti můžeme použít lineární aproximační vzorec k prokázání pravidla známého jako pravidlo L ‚ Hospital. Zde je návod, jak důkaz funguje.
Připomeňme, že lineární aproximace vzorec je:

vidíme, že můžeme změnit vzorec tak, že:
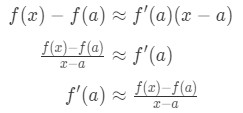
uvědomte si, že sbližování se stává více a více přesné, jak jsme se vybrat hodnoty x, které jsou bližší. Jinými slovy, pokud bereme, že limita pro x→a, pak budou rovné. Takže
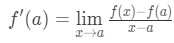
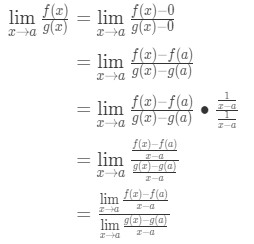
Nyní si všimněte, že můžeme aplikovat vzorec, který jsme odvodili dříve tady. Takže teď
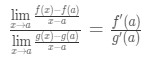
Teď, místo psaní f'(a) g'(a), můžeme použít limity x→a (protože víme, že f a g jsou diferencovatelné)., Takže
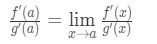
Proto, jen jsme ukázali, že:
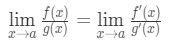
což je L’Hospital je Pravidlo .
kdy použít l ‚hopitalovo pravidlo
vždy chceme použít l‘ hoptialovo pravidlo, když narazíme na neurčité limity. Existují dva typy neurčitých forem., Tyto neurčité formy by bylo:
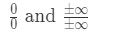
mnoho lidí dělají tu chybu, pomocí l ‚ hospitalovo pravidlo i bez kontroly, pokud se jedná o neurčitou limitu. Takže se ujistěte, že to nejprve zkontrolujete! V opačném případě to nebude fungovat a dostanete špatnou odpověď. Zde je návod k použití pravidla l ‚ Hopital:
- Krok 1: vyhodnoťte limit přímo.
- Krok 2: Zkontrolujte, zda se jedná o jednu z neurčitých forem. Pokud ano, přejděte ke kroku 3.,
- Krok 3: Použijte pravidlo l ‚ Hospital.
- Krok 4: Zkontrolujte, zda máte další neurčitý formulář. Opakujte krok 3, Pokud tak učiníte.
podívejme se na několik příkladů pomocí těchto kroků.
Otázka 6: vypočítat limitu
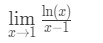
- Krok 1: Vyhodnocení limit přímo nám dává
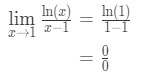
Rovnice 9: L ‚ hospitalovo pravidlo otázka, pt.,2 - Krok 2:
Ano, Je to jedna z neurčitých forem.
- Krok č. 3:
Použitím l ‚ hospitalova pravidla máme:
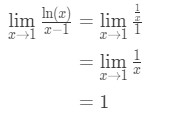
Rovnice 9: L ‚ hospitalovo pravidlo otázka, pt.3 - Krok 4:
jeden není neurčitá forma, takže jsme hotovi a odpověď je 1.
nyní byla tato otázka trochu snadná, tak proč se nepodíváme na něco, co je trochu těžší.,
Otázka 7: vypočítat limitu
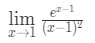
- Krok 1: Vyhodnocení limit přímo vidíme, že:
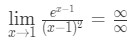
Rovnice 10: L ‚ hospitalovo pravidlo dvakrát otázku pt.2 - Krok 2:
jedná se o neurčitou formu, takže přejděte ke kroku 3.,
- Krok č. 3:
Použitím l ‚ hospitalova pravidla máme,
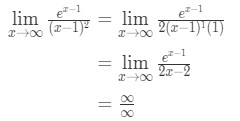
Rovnice 10: L ‚ hospitalovo pravidlo dvakrát otázku pt.3 - Krok 4:
Toto je další neurčitá forma. Takže se musíme vrátit ke kroku 3 a znovu použít pravidla l ‚ hoptialu.
- Krok č. 3:
Použitím l ‚ hospitalovo pravidlo ještě jednou máme:
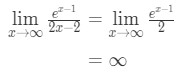
Rovnice 10: L ‚ hospitalovo pravidlo dvakrát otázku pt.,4 - Krok 4:
Nekonečno je neurčitý formě, tak jsme udělali a odpověď je ∞\infty∞