después del radio y diámetro, otra parte importante de un círculo es un arco. En este artículo, discutiremos en detalle qué es un arco, cómo encontrar la longitud de un arco y la medición de la longitud de un arco en radianes. También estudiaremos sobre el arco menor y el arco mayor.
¿Qué es un Arco de un Círculo?
Un arco de un círculo es cualquier porción de la circunferencia de un círculo. Para recordar, la circunferencia de un círculo es el perímetro o la distancia alrededor de un círculo., Por lo tanto, podemos decir que la circunferencia de un círculo es el arco completo del círculo.
¿Cómo Encontrar la Longitud de un Arco?
La fórmula para calcular el arco se establece que:
longitud de Arco = 2nr (θ/360)
Donde, r = es el radio del círculo,
π = pi = 3.14
θ = el ángulo (en grados) subtendido por un arco en el centro del círculo.
360 = el ángulo de una rotación completa.
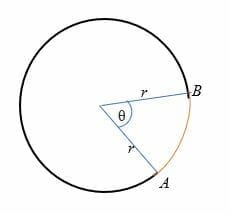
de la ilustración anterior, la longitud del arco (dibujada en rojo) es la distancia del punto A al punto B.,
vamos a resolver algunos problemas de ejemplo sobre la longitud de un arco:
Ejemplo 1
dado que arc AB subtienda un ángulo de 40 grados al centro de un círculo cuyo radio es de 7 cm. Calcular la longitud del arco AB.
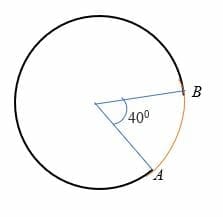
Solución
Dado r = 7 cm
θ = 40 grados.
Por sustitución,
La longitud de un arco = 2nr(θ/360)
Longitud = 2 x 3.14 x 7 x 40/360
= 4.884 cm.
Ejemplo 2
encuentra la longitud de un arco de un círculo que subtienda un ángulo de 120 grados al centro de un círculo cuyo radio es de 24 cm.,
Solución
La longitud de un arco = 2nr(θ/360)
= 2 x 3.14 x 24 x 120/360
= 50.24 cm.
Ejemplo 3
La longitud de un arco es de 35 m. si el radio del círculo es de 14 m, encuentre el ángulo subtendido por el arco.
Solución
La longitud de un arco = 2nr(θ/360)
35 m = 2 x 3.14 x 14 x (θ/360)
35 = 87.92 θ/360
Multiplique ambos lados por 360 para eliminar la fracción.
12600 = 87.92 θ
Divide ambos lados por 87.92
θ = 143.3 grados.,
Ejemplo 4
encuentre el radio de un arco que es de 156 cm de longitud y subestima un ángulo de 150 grados al centro de un círculo.
Solución
La longitud de un arco = 2nr(θ/360)
156 cm = 2 x 3.14 x r x 150/360
156 = 2.6167 r
Divide ambos lados por 2.6167
r = 59.62 cm.
entonces, el radio del arco es de 59.62 cm.
¿cómo encontrar la longitud del arco en radianes?
existe una relación entre el ángulo subtendido por un arco en radianes y la relación entre la longitud del arco y el radio del círculo., En este caso,
θ = (La longitud de un arco) / (el radio del círculo).
por lo Tanto, la longitud de arco en radianes está dada por,
S = r θ
donde, θ = ángulo subtendido por un arco en radianes
S = longitud del arco.
r = radio del círculo.
un radián es el ángulo central subtendido por una longitud de arco de un radio, es decir, s = r
el radián es solo otra forma de medir el tamaño de un ángulo. Por ejemplo, para convertir ángulos de grados a radianes, multiplique el ángulo (en grados) por π/180.,
de manera similar, para convertir radianes a grados, multiplique el ángulo (en radianes) por 180/π
Ejemplo 5
encuentre la longitud de un arco cuyo radio es 10 cm y el ángulo subtendido es 0.349 radianes.
Solution
Arc length = R θ
= 0.349 x 10
= 3.49 cm.
Ejemplo 6
Encontrar la longitud de un arco en radianes, que tiene un radio de 10 m y un ángulo de 2.356 radianes.
Solución
longitud de Arco = r θ
= 10 m x 2.356
= 23.56 m.
Ejemplo 7
Encontrar el ángulo subtendido por un arco que tiene una longitud de 10,05 mm y un radio de 8 mm.,
Solución
longitud de Arco = r θ
10.05 = 8 θ
Divide ambos lados por 8.
1.2567 = θ
Allí, el ángulo subtendido por el arco es 1.2567 radianes.
Ejemplo 8
calcular el radio de un círculo cuya longitud de arco es de 144 yardas y el ángulo de arco, es de 3.665 radianes.
Solution
Arc length = R θ
144 = 3.665 R
Divide ambos lados por 3.665.
144/3.665 = r
r = 39.29 yardas.
Ejemplo 9
calcular la longitud de un arco que subtienda un ángulo de 6.283 radianes al centro de un círculo que tiene un radio de 28 cm.,
Solution
Arc length = R θ
= 28 x 6.283
= 175.93 cm
arco menor (h3)
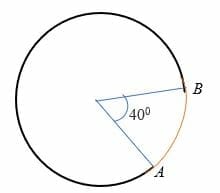
El arco menor es un arco que subtienda un ángulo de menos de 180 grados al centro del círculo. En otras palabras, el arco menor medida menos que un semicírculo y está representado en el círculo por dos puntos. Por ejemplo, el arco AB en el círculo de abajo es el arco menor.
el arco Mayor (h3)
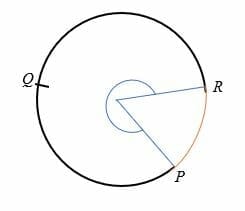
El gran arco de un círculo es un arco que subtienda un ángulo de más de 180 grados hacia el centro del círculo., El arco mayor es mayor que el semicírculo y está representado por tres puntos en un círculo.
por ejemplo, PQR es el arco mayor del círculo que se muestra a continuación.
problemas de práctica
- encuentre el área del sector del círculo de radio 9 mm. asuma que el ángulo subtendido por este arco en el centro es 30 o.
- La Ciudad A se encuentra al norte de la ciudad B. las latitudes de la ciudad A y la ciudad B son 54 O N y 45 O N respectivamente. ¿Cuál es la distancia Norte-Sur entre las dos ciudades? El radio de la Tierra es de 6400 km.,