nu există o singură strategie pentru traducerea expresiilor matematice în expresii algebrice. Atâta timp cât vă puteți aminti elementele de bază, ar trebui să fie capabil de a aborda cele mai dificile. Doar asigurați-vă că puteți justifica modul în care veniți cu propria expresie algebrică și, mai important, că are sens pentru dvs. Cereți întotdeauna ajutorul profesorilor dvs., după cum este necesar sau colaborați cu colegii de clasă, astfel încât să vă puteți verifica răspunsurile.,pentru a vă construi abilitățile în scrierea expresiilor algebrice, vom parcurge diferite moduri în care fiecare operație poate apărea ca un cuvânt sau o expresie în problemă. Cele patru operații aritmetice implicate sunt adunarea, scăderea, înmulțirea și împărțirea.,
Key Words for Addition

Key Words for Subtraction

Key Words for Multiplication

Key Words for Division

It is time now time to go over some examples to practice writing algebraic expressions., Am separa exemplele în două:
- Exemple de bază de expresii algebrice
- Exemple multiple de expresii algebrice
Exemple de expresii algebrice de bază
Exemplul 1: Scrieți o expresie algebrică pentru expresia matematică „suma unui număr și a patru”.
soluție: cuvântul „sumă” ne dă imediat indiciul pe care îl vom adăuga aici. Observați că dorim să adăugăm două cantități: un număr necunoscut și numărul 4. Deoarece nu știm care este valoarea numărului, putem folosi o variabilă pentru a o reprezenta., Puteți utiliza orice litere ale alfabetului. În acest caz, să fim de acord să folosim Y pentru variabilă.
când adăugăm variabila y și 4, avem y + 4. De asemenea, este bine să scrieți răspunsul dvs. ca 4 + y, deoarece adăugarea este comutativă – adică schimbarea ordinii de adăugare nu își schimbă suma.
răspunsul final este y+4.exemplul 2: Scrieți o expresie algebrică pentru expresia matematică „10 crescut cu un număr”.
soluție: cuvintele cheie „crescute cu” implică adăugarea. Aceasta înseamnă că un număr necunoscut a fost adăugat la 10., Folosind litera k ca variabilă, putem traduce Declarația de mai sus ca 10 + k. deoarece adăugarea este comutativă, o putem rescrie ca k + 10. Oricare dintre cele două de mai sus este un răspuns corect.răspunsul final este k+10.exemplul 3: Scrieți o expresie algebrică pentru expresia matematică „diferența de 1 și un număr”.
soluție: cuvântul „diferență” sugerează că vom scădea. În plus, atunci când vă confruntați cu acest cuvânt matematica (diferență) asigurați-vă că să acorde o atenție la ordinea. Numărul 1 vine mai întâi, apoi un număr necunoscut vine în al doilea rând., Asta înseamnă că numărul 1 este minuend și numărul necunoscut este subtrahend. Dacă decidem să folosim litera x ca variabilă, răspunsul devine 1 − x.
răspunsul final este 1 – x.
Exemplul 4: Scrieți o expresie algebrică pentru expresia matematică „un număr mai mic de 8”.soluție: fiți foarte atenți atunci când aveți de-a face cu cuvintele cheie „mai puțin de”. Prima cantitate care vine înainte de cuvintele cheie” mai puțin decât „care este” un număr ” este subtrahend. În timp ce cantitatea care vine după ce devine minuend.,cu alte cuvinte, vom scădea numărul necunoscut din numărul 8. Dacă alegem variabila noastră să fie litera a, obținem 8-a.
răspunsul final este 8-a.
exemplul 5: scrieți o expresie algebrică pentru expresia matematică „produsul 5 și un număr”.soluție: pentru a găsi produsul a două cantități sau valori, înseamnă că le vom multiplica împreună. Selectând litera m ca variabilă, expresia algebrică pentru această frază matematică este pur și simplu 5m. înseamnă de 5 ori numărul necunoscut m.
răspunsul final este 5m.,exemplul 6: scrieți o expresie algebrică pentru expresia matematică”de două ori un număr”.soluție: cuvântul „de două ori” înseamnă că vom dubla ceva. În acest caz, dorim să dublăm o valoare sau o cantitate necunoscută. Fie litera d numărul necunoscut, când o dublăm obținem expresia algebrică 2D.
răspunsul final este 2d.
exemplul 7: scrieți o expresie algebrică pentru expresia matematică „coeficientul unui număr și 7”.
soluție: cuvântul cheie „coeficient” înseamnă că efectuăm operațiunea de divizare. Vom împărți un număr necunoscut cu 7., Alegerea literei w ca variabilă, fraza matematică de mai sus poate fi exprimată ca expresie algebrică de mai jos.exemplul 8: scrieți o expresie algebrică pentru expresia matematică”raportul dintre 10 și un număr”.soluție: în mod similar, cuvântul „raport” înseamnă diviziune. Ordinea aici este foarte importantă. Prima cantitate este numărul 10, iar a doua cantitate este numărul necunoscut. Asta înseamnă că 10 este împărțit la un număr necunoscut., Fie c numărul necunoscut, expresia algebrică pentru fraza matematică de mai sus poate fi scrisă ca
\LARGE{10 \over c}
Exemple de expresii algebrice cu mai multe părți
de data aceasta, ne vom ocupa de fraze matematice care sunt puțin mai complexe. Expresiile algebrice de aici pot conține două sau mai multe operații. Cuvintele cheie de bază pe care le învățăm înainte vor servi drept fundație pe măsură ce lucrăm cu frazele matematice mai provocatoare pentru a interpreta în expresii algebrice.,
Exemplul 1: Scrieți o expresie algebrică pentru expresia matematică „3 mai mult de două ori un număr”.soluție: pentru a face acest lucru mult mai ușor de înțeles, vom împărți această frază în două părți. În primul rând, recunoașteți că avem un număr necunoscut. O putem reprezenta prin orice litere ale alfabetului. Fie ca numărul necunoscut să fie variabila x. diagrama de mai jos ar trebui să ne ajute să vedem ce se întâmplă cu adevărat.,
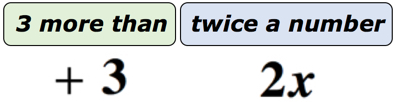
Dacă te gândești la asta, există un număr necunoscut reprezentat de variabila x, care este de a fi dublate sau multiplicate cu 2. Oricare ar fi produsul, vom adăuga 3 la acesta. Deci, răspunsul nostru final ar trebui să arate ca cel de mai jos.răspunsul final este 2x+3.exemplul 2: Scrieți o expresie algebrică pentru expresia matematică”diferența dintre jumătate de număr și 10″.
soluție: să presupunem că variabila y este numărul necunoscut., Cuvântul cheie „diferență” ne solicită că vom efectua scăderea. Este esențial aici să acordăm atenție ordinii de scădere. După cuvântul „diferență”, ar trebui să ne așteptăm la două cantități. Primul va fi minuend, în timp ce al doilea va fi subtrahend. Aruncați o privire la diagrama de mai jos.
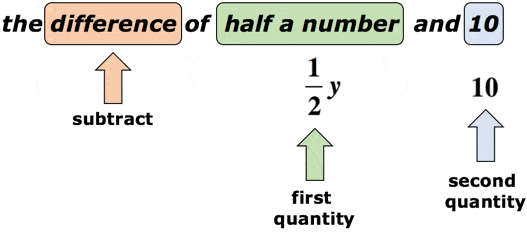
Referindu-se la diagrama de mai sus, vom scădea prima cantitate de cel de-al doilea cantitate. Cu alte cuvinte, a doua cantitate este scăzută din prima cantitate., Răspunsul final pentru matematica expresie-ar place ceva de genul asta,
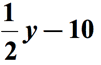
Exemplul 3: Scrieți o expresie algebrică pentru matematica fraza „7 mai mic decât produsul dintre un număr și 6”.
soluție: știm că „mai puțin de” Sugerează o operație de scădere. Dar trebuie să fim puțin atenți aici, deoarece ordinea cu privire la modul în care scădem este importantă. Să presupunem că numărul necunoscut este reprezentat de variabila k. să punem acest lucru pe o diagramă pentru a înțelege acest lucru.,
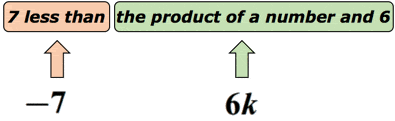
de Fapt, această expresie matematica poate fi rescrisă ca
” produsul dintre un număr și 6 minus 7 „
„7 mai puțin decât” înseamnă „minus 7” la orice cantitate de descris, care în acest caz „produsul dintre un număr și 6”. Iată interpretarea finală a expresiei matematice într-o expresie algebrică:
6k-7
Exemplul 4: Scrieți o expresie algebrică pentru expresia matematică „media unui număr și 4”.,soluție: pentru a începe această frază matematică specială, trebuie să revizuim ce înseamnă cuvântul „mediu”. Pentru a calcula media sau media a două sau mai multe numere, va trebui să adăugăm toate numerele pentru a obține o sumă, apoi să o împărțim după numărul de intrări sau câte numere există. Dacă lăsăm M să fie variabila pentru a reprezenta numărul necunoscut, expresia matematică de mai sus poate fi exprimată în expresii algebrice ca,
\LARGE{{m + 4} \over 2}
exemplul 5: scrieți o expresie algebrică pentru expresia matematică „coeficientul de 1 și 1 a scăzut cu un număr”.,
soluție: cuvântul cheie „coeficient” înseamnă că vom împărți. În acest caz, dorim să împărțim numărul 1 cu cantitatea 1 scăzută cu un număr. Mai jos este expresia algebrică care poate reprezenta fraza matematică de mai sus. Să fie un număr necunoscut.
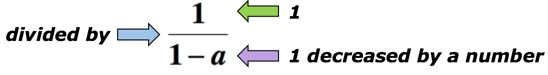
Exemplul 6: Scrie o expresie algebrică pentru matematica fraza „o treime din pătrată a unui număr crescut de 2”.
soluție: există câteva lucruri se întâmplă aici., În primul rând, partea frazei care afirmă „o treime din pătratul unui număr” poate fi interpretată ca „pătratul unui număr împărțit la 3”. Va trebui să ridicăm numărul necunoscut cu 2, apoi Să împărțim cu 3. Să presupunem că numărul necunoscut este t, obținem
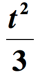
nu Am terminat încă. Ultimul pas de făcut este să adăugați cantitatea de mai sus cu 2 pentru a încorpora partea rămasă a expresiei ” crescută cu 2 „. Iată deci reprezentarea finală a expresiei matematice date.,
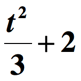
You might also be interested in:
Algebraic Expressions
Algebraic Sentences Word Problems