Po promieniu i średnicy kolejną ważną częścią okręgu jest łuk. W tym artykule omówimy szczegółowo, czym jest łuk, jak znaleźć długość łuku i pomiar długości łuku w radianach. Będziemy również badać łuk minorowy i Łuk główny.
Co to jest łuk koła?
łuk okręgu to dowolna część obwodu okręgu. Przypomnijmy, Obwód okręgu to obwód lub odległość wokół okręgu., Dlatego możemy powiedzieć, że obwód okręgu jest pełnym łukiem samego okręgu.
jak znaleźć Długość łuku?
wzór do obliczania łuku stwierdza, że:
długość łuku = 2NR (θ/360)
Gdzie, R = promień okręgu,
π = pi = 3.14
θ = kąt (w stopniach) mniejszy od Łuku w środku okręgu.
360 = kąt jednego pełnego obrotu.
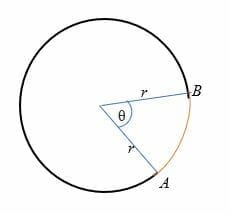
na powyższej ilustracji długość łuku (narysowana na Czerwono) jest odległością od punktu A do punktu B.,
rozwiążmy kilka przykładowych problemów dotyczących długości łuku:
przykład 1
biorąc pod uwagę, że łuk AB obniża kąt 40 stopni do środka okręgu, którego promień wynosi 7 cm. Oblicz Długość ŁUKU AB.
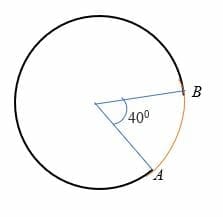
rozwiązanie
Podane r = 7 cm
θ = 40 stopni.
przez podstawienie,
długość łuku = 2NR(θ/360)
długość = 2 x 3,14 x 7 x 40/360
= 4,884 cm.
przykład 2
Znajdź długość łuku okręgu, który obniża kąt 120 stopni do środka okręgu, którego promień wynosi 24 cm.,
długość łuku = 2NR (θ/360)
= 2 x 3,14 x 24 x 120/360
= 50,24 cm.
przykład 3
długość łuku wynosi 35 m. jeśli promień okręgu wynosi 14 m, Znajdź kąt nachylony przez łuk.
rozwiązanie
długość łuku = 2NR(θ/360)
35 m = 2 x 3,14 x 14 x (θ/360)
35 = 87,92 θ/360
pomnóż obie strony przez 360, aby usunąć ułamek.
12600 = 87.92 θ
podziel obie strony przez 87.92
θ = 143.3 stopni.,
przykład 4
Znajdź promień łuku o długości 156 cm i podciąga kąt 150 stopni do środka okręgu.
rozwiązanie
długość łuku = 2NR(θ/360)
156 cm = 2 x 3,14 x r x 150/360
156 = 2,6167 r
podziel obie strony przez 2,6167
r = 59,62 cm.
promień łuku wynosi więc 59,62 cm.
jak znaleźć Długość łuku w radianach?
istnieje zależność między kątem podanym przez łuk w radianach a stosunkiem długości łuku do promienia okręgu., W tym przypadku
θ = (Długość łuku) / (promień okręgu).
dlatego długość łuku w radianach jest określona przez,
S = R θ
gdzie, θ = kąt nachylenia łuku w radianach
S = Długość łuku.
r = promień okręgu.
jeden radian to kąt centralny pomniejszony o długość łuku o jeden promień, tzn. s = r
radian to kolejny sposób pomiaru wielkości kąta. Na przykład, aby przekształcić kąty ze stopni na radiany, pomnóż kąt (w stopniach) przez π/180.,
podobnie, aby przeliczyć radiany na stopnie, pomnóż kąt (w radianach) przez 180/π
przykład 5
Znajdź długość łuku, którego promień wynosi 10 cm, a kąt nachylenia wynosi 0,349 radianów.
długość łuku = r
= 0,349 x 10
= 3,49 cm.
przykład 6
Znajdź długość łuku w radianach, która ma promień 10 m i kąt 2,356 radianów.
rozwiązanie
długość łuku = r θ
= 10 m x 2.356
= 23.56 m.
przykład 7
Znajdź kąt nachylony przez łuk o długości 10.05 mm i promieniu 8 mm.,
rozwiązanie
długość łuku = r θ
10.05 = 8 θ
podziel obie strony przez 8.
1,2567 = θ
tam kąt nachylenia łuku wynosi 1,2567 radianów.
przykład 8
Oblicz promień okręgu, którego długość łuku wynosi 144 jardów, a kąt łuku wynosi 3,665 radianów.
rozwiązanie
długość łuku = r θ
144 = 3,665 r
podziel obie strony przez 3,665.
144/3.665 = r
r = 39.29 jardów.
przykład 9
Oblicz długość łuku, który obniża kąt 6.283 radianów do środka okręgu o promieniu 28 cm.,
rozwiązanie
długość łuku = r θ
= 28 x 6.283
= 175.93 cm
Łuk Minorowy (h3)
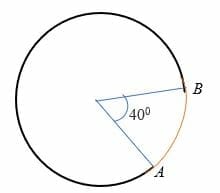
łuk minorowy jest łukiem, który obniża kąt mniejszy niż 180 stopni do środka okręgu. Innymi słowy, łuk mniejszy mierzy mniej niż półkole i jest reprezentowany na okręgu przez dwa punkty. Na przykład łuk AB w okręgu poniżej jest łukiem podrzędnym.
Łuk główny (h3)
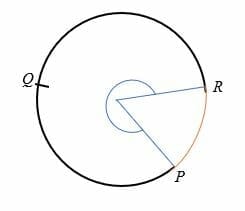
łuk główny okręgu to łuk, który obniża kąt większy niż 180 stopni do środka okręgu., Łuk główny jest większy od półkola i jest reprezentowany przez trzy punkty na okręgu.
na przykład PQR jest głównym łukiem okręgu pokazanego poniżej.
problemy praktyczne
- znajdź obszar sektora okręgu o promieniu 9 mm. Załóżmy, że kąt nachylony przez ten łuk w centrum wynosi 30 o.
- Miasto A znajduje się na północ od miasta B. szerokości geograficzne miasta a i miasta B wynoszą odpowiednio 54 o N I 45 o N. Jaka jest odległość Północ-Południe między tymi dwoma miastami? Promień Ziemi wynosi 6400 km.,