Załóżmy, że chcesz wziąć pod uwagę wpływ czynnika ryzyka na czas do wystąpienia zdarzenia. Na przykład Arnlov i wsp (2010) rozważają wpływ wskaźnika masy ciała (BMI) i zespołu metabolicznego na rozwój chorób układu krążenia i zgonów u mężczyzn w średnim wieku. Stowarzyszenia zostały zbadane na podstawie danych z badania kohortowego 1758 Szwedzkich mężczyzn w średnim wieku mieszkających w jednym hrabstwie z ponad 30 lat obserwacji., Poniższy rysunek przedstawia czas do poważnego zdarzenia sercowo-naczyniowego według kategorii BMI i obecności (B) lub braku (a) zespołu metabolicznego. Czy jest jakaś różnica w tych krzywych przetrwania?

rycina 2: krzywe Kaplana-Meiera dla głównych zdarzeń sercowo-naczyniowych w różnych kategoriach BMI u osób bez MetS (A) i z MetS (B).

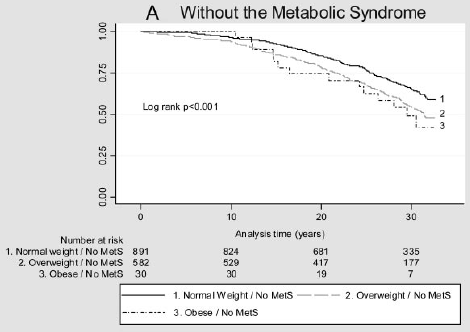
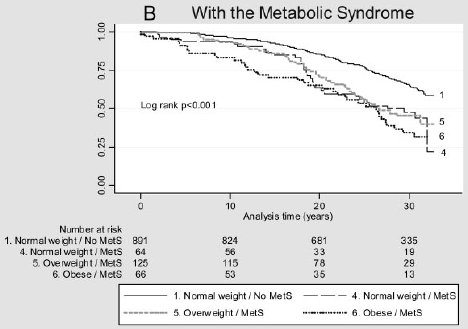
(dane odtworzone z Arnlov, J et al., Wpływ wskaźnika masy ciała i zespołu metabolicznego na ryzyko chorób układu krążenia i zgonów u mężczyzn w średnim wieku. Obieg 2010; 121; 230-236, pierwotnie opublikowany online 12/28/2009; DOI 10.1161/obieg.109.88752)

Czy regresja logistyczna, z BMI jako zmienną predykcyjną, byłaby odpowiednia do analizy tych danych?,

odpowiedź

zależność między obecnością lub brakiem istotnego zdarzenia sercowo-naczyniowego a zmienną predykcyjną można ocenić za pomocą regresji logistycznej w określonym czasie, ale nie porównałoby to bezpośrednio krzywych przeżycia. Analiza przeżycia porównałaby krzywe na podstawie czasu do zdarzenia.

metody analizy przeżycia, takie jak regresja zagrożeń proporcjonalnych, różnią się od regresji logistycznej oceną wskaźnika zamiast proporcji.,

proporcjonalna regresja zagrożeń zwana również regresją Coxa, modeluje częstość występowania lub stopień zagrożenia, liczbę nowych przypadków choroby na populację zagrożoną w jednostce czasu. Jeśli wynikiem jest śmierć, jest to wskaźnik śmiertelności.
funkcja zagrożenia funkcja zagrożenia jest prawdopodobieństwem, że jeśli dana osoba przeżyje do t, doświadczy zdarzenia w następnej chwili.

regresja logistyczna natomiast uwzględnia odsetek nowych przypadków, które rozwijają się w danym okresie czasu, tj. skumulowaną częstość występowania., Regresja logistyczna szacuje współczynnik szans; regresja proporcjonalna zagrożeń szacuje współczynnik ryzyka.

stosunek funkcji ryzyka można uznać za stosunek funkcji ryzyka, więc model regresji ryzyka proporcjonalnego można uznać za funkcję ryzyka względnego (podczas gdy modele regresji logistycznej są funkcją wskaźnika kursów). Zmiany współzmienności mają multiplikatywny wpływ na ryzyko wyjściowe. Model pod względem funkcji zagrożenia w czasie t to:

\(\lambda \left ( T|X_{1i},X_{2i},…, X_ {Ki} \ right) = \ lambda_{0} (t)exp \ left (\beta_ {1} X_{1i}+ \ beta_{2} X_{2i}+…,+ \ beta_ {K} X_ {Ki} \right)\)

chociaż żaden konkretny model prawdopodobieństwa nie został wybrany, aby reprezentować czas przeżycia, regresja proporcjonalnych zagrożeń ma ważne założenie: zagrożenie dla każdej osoby jest stałą proporcją zagrożenia dla każdej innej osoby. (tj. zagrożenia proporcjonalne)., Zauważ, że jeśli \(\lambda_0 (t)\) Jest funkcją zagrożenia dla podmiotu o wszystkich wartościach predykcyjnych równych zero, a \(\lambda_1 (T)\) Jest funkcją zagrożenia dla podmiotu o innych wartościach dla zmiennych predykcyjnych, to współczynnik ryzyka zależy tylko od zmiennych predykcyjnych, a nie od czasu t. założenie to oznacza, że jeśli kowariantna podwaja ryzyko zdarzenia w pierwszym dniu, podwaja również ryzyko zdarzenia w dowolnym innym dniu.,

modele zagrożeń proporcjonalnych mogą być używane do dyskretnych lub ciągłych miar czasu zdarzenia i mogą zawierać współzmienniki zależne od czasu (kowarianty, których wartości mogą ulec zmianie w okresie obserwacji). Stosując regresję zagrożeń proporcjonalnych, można wytworzyć współczynniki zagrożenia (lub ryzyka) dostosowane do kowariancji.

wróćmy do pierwotnego pytania zadanego przez Arnlova i colleagues…do BMI i zespół metaboliczny wpływają na rozwój chorób układu krążenia? Przeczytaj Arnlov et al., Impact of Body Mass Index and the Metabolic Syndrome on the Risk of Cardiovascular Disease and Death in Middle Aged Men Circulation 2010; 121; 230-236, ze szczególnym uwzględnieniem metod statystycznych, wyników i wniosków.

Porównaj i skontrastuj podejście regresji proporcjonalnej zagrożeń z podejściem regresji logistycznej, czytając Franco et al. Trajektorie wejścia w zespół metaboliczny: badanie serca Framingham. Obieg 2009;120; 1943-1950; originally published online Nov 2, 2009; American Heart Association. 7272 Greenville Avenue, Dallas, TX DOI: 10.,1161 / cyrkulacji.109.855817

można również porównać wyniki obu badań. Obie gazety są w folderze odczytów na tydzień 14.

Uwaga! Jeśli nie jesteś zaznajomiony z krzywymi Kaplana-Meiera, przeczytaj rozdział analizy przeżycia w monografii metody badawcze II z Journal of Tropical Pediatrics

(dostęp od http://www.oxfordjournals.org/our_journals/tropej/online/ma_chap12.pdf)