Det er ingen enkel strategi for å oversette matematiske uttrykk i algebraiske uttrykk. Så lenge du kan huske det grunnleggende, du bør være i stand til å takle mer utfordrende stier. Bare sørg for at du kan rettferdiggjøre hvordan du kommer opp med din egen algebraiske uttrykk, og enda viktigere at det er fornuftig for deg. Alltid be om hjelp fra lærerne når det er nødvendig eller samarbeide med dine klassekamerater, slik at du kan kontrollere dine svar.,
for Å bygge dine ferdigheter i skriving algebraiske uttrykk, vil vi gå over ulike måter på hvordan hver operasjon kan dukke opp som et ord eller en frase i problemet. De fire aritmetiske operasjonene som er involvert, addisjon, subtraksjon, multiplikasjon og divisjon.,
Key Words for Addition

Key Words for Subtraction

Key Words for Multiplication

Key Words for Division

It is time now time to go over some examples to practice writing algebraic expressions., Jeg skille eksempler i to:
- Grunnleggende eksempler på algebraiske uttrykk
- Multi-del eksempler på algebraiske uttrykk
Grunnleggende Algebraiske Uttrykk Eksempler
Eksempel 1: Skriv et algebraisk uttrykk for matematiske uttrykket «summen av en rekke og fire».
Løsning: ordet «sum» umiddelbart gir oss hint om at vi kommer til å legge til her. Legg merke til at vi ønsker å legge til to mengder: ett ukjent nummer og nummer 4. Siden vi ikke vet hva verdien av nummeret, kan vi bruke en variabel til å representere den., Du kan bruke alle bokstavene i alfabetet. I dette tilfellet, la oss enige om å bruke y for variabelen.
Når vi legger til den variable y og 4, har vi y + 4. Det er også greit å skrive svaret ditt som 4 + y grunn tillegg er kommutative, som er å bytte om på rekkefølgen av tillegg endrer ikke sin sum.
Det endelige svaret er y+4.
Eksempel 2: Skrive et algebraisk uttrykk for matematiske uttrykket «10 økt med et tall».
Løsning: søkeordene «, økte med» antyder tillegg. Dette betyr at et ukjent antall har blitt lagt til 10., Ved hjelp av bokstaven k som variabel, kan vi oversette setningen ovenfor som 10 + k. Siden tillegg er kommutative, vi kan skrive om det som k + 10. En av de to ovenfor er et riktig svar.
Det endelige svaret er k+10.
Eksempel 3: Skrive et algebraisk uttrykk for matematiske uttrykket «det forskjell på 1 og et tall».
Løsning: ordet «forskjell» tyder på at vi kommer til å trekke fra. I tillegg, når du opplever dette matte ord (forskjellen) sørg for å ta hensyn til rekkefølgen. Nummer 1 kommer først, deretter et ukjent nummer kommer i andre., Det betyr at den nummer 1 er minuend og ukjent antall er subtrahend. Hvis vi bestemmer oss for å bruke bokstaven x-som vår variabel, svaret blir 1 − x.
Det endelige svaret er 1 – x.
Eksempel 4: Skrive et algebraisk uttrykk for matematiske uttrykket «et tall mindre enn 8».
Løsning: Vær svært forsiktig når du arbeider med søkeordene «mindre enn». Den første kvantum som kommer før «mindre enn» søkeord som er «et nummer» er subtrahend. Mens antallet som kommer etter det blir det minuend.,
med andre ord, vi kommer til å trekke ukjent nummer fra nummer 8. Hvis vi velger våre variabel til å være bokstav a, får vi 8 − en.
Det endelige svaret er 8 – en.
Eksempel 5: Skrive et algebraisk uttrykk for matematiske uttrykket «produktet av 5 og et tall».
Løsning: for Å finne et produkt av to mengder eller verdier, det betyr at vi vil multiplisere dem sammen. Å velge den bokstaven m som vår variabel, den algebraiske uttrykk for denne matematiske uttrykket er rett og slett 5m. Det betyr 5 ganger ukjent antall m.
Det endelige svaret er 5m.,
Eksempel 6: Skrive et algebraisk uttrykk for matematiske uttrykket «to ganger et tall».
Løsning: ordet «to ganger» betyr at vi kommer til å doble noe. I dette tilfellet ønsker vi å doble en ukjent verdi eller mengde. La bokstav d være ukjent nummer, når vi doble det får vi den algebraiske uttrykk 2d.
Det endelige svaret er 2d.
Eksempel 7: Skrive et algebraisk uttrykk for matematiske uttrykket «kvotienten av et nummer og 7».
Løsning: søkeordet «quotient» betyr at vi utfører drift av avdelingen. Vi vil dele et ukjent antall av 7., Ved å velge bokstaven w som vår variabel, det matematiske uttrykket over kan være uttrykt som den algebraiske uttrykk nedenfor.
\LARGE{w \over 7}
Eksempel 8: Skriv et algebraisk uttrykk for matematiske uttrykket «forholdet mellom 10 og et tall».
Løsning: på samme måte, ordet «forhold» betyr divisjon. Rekkefølgen her er veldig viktig. Den første kvantitet er nummer 10 og den andre mengden er ukjent nummer. Det betyr at 10 er delt av et ukjent nummer., La c være ukjent nummer, den algebraiske uttrykk for matematiske uttrykket over kan skrives som
\LARGE{10 \over c}
Multi-Del Algebraiske Uttrykk Eksempler
Denne gangen, vil vi avtale med matematiske uttrykk som er litt mer komplisert. Den algebraiske uttrykk her kan inneholde to eller flere operasjoner. Den grunnleggende søkeord som vi lærer før vil tjene som grunnlag når vi jobber på med mer utfordrende matematiske setninger for å tolke inn algebraiske uttrykk.,
Eksempel 1: Skriv et algebraisk uttrykk for matematiske uttrykket «3 mer enn to ganger et tall».
Løsning: for Å gjøre dette mye enklere å forstå, vi kommer til å dele dette uttrykket inn i to deler. Først erkjenne at vi har et ukjent nummer. Vi kan vise det ved alle bokstavene i alfabetet. La ukjent antall være variabel x. Diagrammet nedenfor skal hjelpe oss til å se hva som egentlig foregår.,
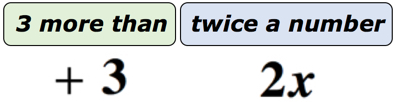
Hvis du tenker på det, det er et ukjent antall representert ved variabel x som blir doblet eller multiplisert med 2. Hva er produktet, vil vi legge til 3 til det. Så, endelig svar skal se ut som den nedenfor.
Det endelige svaret er 2x+3.
Eksempel 2: Skrive et algebraisk uttrykk for matematiske uttrykket «forskjellen på et halvt nummer og 10».
Løsning: la oss Anta at variabelen y er ukjent nummer., Søkeordet «forskjell» ber oss at vi kommer til å utføre subtraksjon. Det er viktig her at vi ta hensyn til rekkefølgen av subtraksjon. Etter ordet «forskjell», bør vi forvente to mengder. Den første vil være den minuend, mens andre vil være subtrahend. Ta en titt på diagrammet nedenfor.
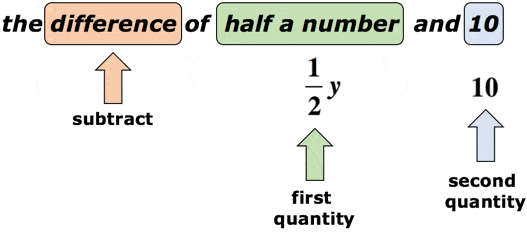
Refererer til diagrammet ovenfor, vil vi trekke fra den første kvantum av den andre kvantitet. Med andre ord, det andre mengde trekkes fra den første kvantitet., Det endelige svaret for matematiske uttrykket skulle gjerne noe sånt som dette,
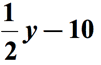
Eksempel 3: Skrive et algebraisk uttrykk for matematiske uttrykket «7 mindre enn produktet av et tall og 6».
Løsning: Vi vet at «mindre enn» antyder en subtraksjon drift. Men vi må være litt forsiktig her, fordi rekkefølgen på hvordan vi trekke fra er viktig. Antar det ukjente nummeret er representert ved variabelen k. La oss sette dette på et diagram for å gjøre en følelse av det.,
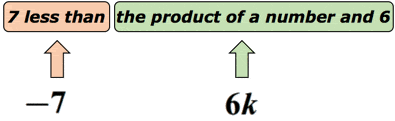
Faktisk, denne matematiske uttrykk kan være omskrevet som
» produktet av et tall og 6 minus 7 «
«7 mindre enn» betyr «minus 7» til det antall som blir beskrevet som i dette tilfellet «produktet av et tall og 6». Her er den endelige tolkningen av matematiske uttrykk i et algebraisk uttrykk:
6k-7
Eksempel 4: Skrive et algebraisk uttrykk for matematiske uttrykket «gjennomsnittet av antall og 4».,
Løsning: for Å komme i gang på denne spesielle matematiske uttrykk, må vi vurdere hva ordet «gjennomsnittlig» betyr. For å beregne gjennomsnittlig eller gjennomsnittet av to eller flere tall, må vi legge sammen alle tallene til å få en sum deretter divideres det med antall oppføringer, eller hvor mange tall det er. Hvis vi la m være den variabelen som skal representere ukjent nummer, det matematiske uttrykket over kan bli uttrykt i algebraiske uttrykk som,
\LARGE{{m + 4} \over 2}
Eksempel 5: Skrive et algebraisk uttrykk for matematiske uttrykket «kvotienten av 1, og 1 er redusert med et tall».,
Løsning: søkeordet «quotient» betyr at vi vil dele. I dette tilfellet ønsker vi å dele antall 1 av antall 1 redusert med et nummer. Nedenfor er den algebraiske uttrykk som representerer det matematiske uttrykket ovenfor. La a være den ukjente nummer.
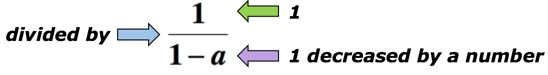
Eksempel 6: Skrive et algebraisk uttrykk for matematiske uttrykket «en tredjedel av kvadratet av et tall, økte med 2».
Løsning: Det er et par ting her., Første, den delen av uttrykket som sier «en tredjedel av kvadratet av et tall» kan tolkes som » kvadratet av et tall dividert med 3 «. Vi trenger å heve ukjent antall av 2 deler med 3. Antar det ukjente nummeret er t, får vi
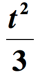
Vi er ikke ferdig ennå. Det siste trinnet å gjøre er å legge til kvantitet over av 2 til å innlemme den gjenværende del av frasen «, økte med 2 «. Så her er den endelige representasjon av gitt matematiske uttrykk.,
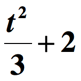
You might also be interested in:
Algebraic Expressions
Algebraic Sentences Word Problems