数学のフレーズを代数式に変換するための単一の戦略はありません。 あなたが基本を覚えている限り、あなたはより挑戦的なものに取り組むことができるはずです。 あなた自身の代数的表現をどのように思いつくかを正当化できること、そしてもっと重要なことはそれがあなたにとって理にかなっていることを あなたの答えを確認できるように、必要に応じて常に教師からの助けを求めるか、クラスメートと協力してください。,
代数式を書くスキルを構築するために、各操作が問題の単語またはフレーズとしてどのように表示されるかについて、さまざまな方法を説明します。 関係する四つの算術演算は、加算、減算、乗算、および除算です。,
Key Words for Addition

Key Words for Subtraction

Key Words for Multiplication

Key Words for Division

It is time now time to go over some examples to practice writing algebraic expressions., 例を二つに分けます。
- 代数式の基本例
- マルチパート代数式の例
基本的な代数式の例
例1:数学のフレーズ”数と四の合計”の代数式を書きます。
解決策:”sum”という言葉はすぐにここに追加するヒントを与えてくれます。 一つの未知の数と数4:私たちは二つの量を追加したいことに注意してください。 数値の値がわからないので、変数を使用してそれを表すことができます。, アルファベットの任意の文字を使用できます。 この場合、変数にyを使用することに同意しましょう。
変数yと4を追加すると、y+4が得られます。 加算は可換であるため、答えを4+yと書いても大丈夫です–つまり、加算の順序を切り替えてもその合計は変わりません。
最終的な答えはy+4です。
例2:数学フレーズ”10increased by a number”の代数式を記述します。
ソリューション:キーワード”増加した”は、追加を意味します。 これは、未知の番号が10に追加されたことを意味します。, 文字kを変数として使用すると、上記の文を10+kと翻訳できます。加算は可換であるため、k+10と書き換えることができます。 上記の二つのいずれかが正解です。
最終的な答えはk+10です。
例3:数学フレーズ”1と数の差”の代数式を記述します。
解決策:”差”という言葉は、減算することを示唆しています。 また、この数学の単語(違い)に遭遇したときには、順序に注意を払うようにしてください。 番号1が最初に来て、未知の番号が第二に来ます。, つまり、番号1はminuendであり、未知の番号はsubtrahendです。 変数として文字xを使用することを決定した場合、答えは1−xになります。
最終的な答えは1-xです。
例4:数学フレーズ”8未満の数”の代数式を書きます。
解決策:”less than”というキーワードを扱うときは非常に注意してください。 “数値”である”より小さい”キーワードの前に来る最初の量は、サブトラエンドです。 それの後に来る量がminuendになる間。,
言い換えれば、8の数字から未知の数字を引きます。 変数を文字aに選択すると、8−aが得られます。
最終的な答えは8-aです。
例5:数学のフレーズ”5と数字の積”の代数式を記述します。
解決策:二つの量または値の積を見つけるために、それは我々がそれらを一緒に乗算することを意味します。 変数として文字mを選択すると、この数学フレーズの代数式は単に5mです.未知の数mの5倍を意味します.
最終的な答えは5mです。,
例6:数学フレーズ”twice a number”の代数式を記述します。
解決策:”twice”という言葉は、私たちが何かを倍増させることを意味します。 この場合、未知の値または数量を倍増させたいとします。 文字dを未知の数とし、それを倍にすると代数式2dが得られます。
最終的な答えは2dです。
例7:数学のフレーズ”数と7の商”の代数式を書きます。
解決策:キーワード”商”は、除算の操作を実行していることを意味します。 未知の数を7で割ります。, 変数として文字wを選択すると、上記の数学フレーズは以下の代数式として表すことができます。
\LARGE{w\over7}
例8:数学フレーズ”10と数の比率”の代数式を書きます。
解決策:同様に、”比率”という言葉は除算を意味します。 ここでの順序は非常に重要です。 最初の数量は数10であり、第二の数量は未知の数です。 つまり、10を未知の数で割ったものです。, Cを未知の数とすると、上記の数学フレーズの代数式は
\LARGE{10\over c}
マルチパート代数式の例
今回は、もう少し複雑な数学フレーズを扱います。 ここでの代数式は、二つ以上の演算を含むことができます。 私たちが前に学ぶ基本的なキーワードは、代数式に解釈するためのより挑戦的な数学のフレーズで作業するときの基礎となります。,
例1:数学フレーズ”3more than twice a number”の代数式を記述します。
解決策:これをはるかに理解しやすくするために、このフレーズを二つの部分に分割します。 まず、我々は未知の番号を持っていることを認識します。 アルファベットの任意の文字で表現することができます。 以下の図は、実際に何が起こっているのかを見るのに役立つはずです。,
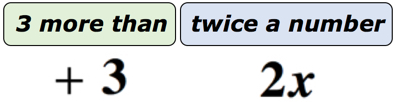
あなたがそれについて考えるならば、変数xで表される未知の数があります2倍または乗算されています。 製品が何であれ、私たちはそれに3を追加します。 だから、私たちの最終的な答えは以下のようになります。
最終的な答えは2x+3です。
例2:数学フレーズ”半分の数と10の差”の代数式を書きます。
解決策:変数yが未知の数であるとします。, キーワード”差”は、減算を実行することを促します。 ここでは、減算の順序に注意を払うことが重要です。 “違い”という言葉の後に、二つの量を期待する必要があります。 最初のものはminuendになり、第二のものはsubtrahendになります。 下の図を見てみましょう。
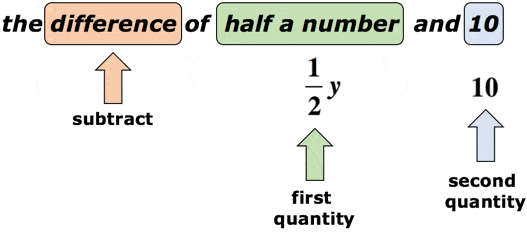
上記の図を参照して、最初の数量を第二の数量で減算します。 言い換えれば、第二の量は、最初の量から減算されます。, 数学のフレーズの最終的な答えは、次のようなものでなければなりません。
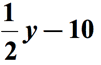
例3:数学のフレーズ”7と6の積よりも小さい”の代数式を記述します。
解決策:”より小さい”は減算演算を示唆していることがわかります。 しかし、減算の順序が重要であるため、ここでは少し注意する必要があります。 未知の数が変数kで表されているとします。,
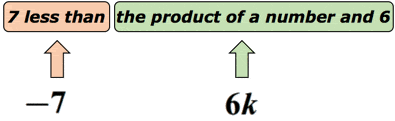
実際には、この数学のフレーズは次のように書き換えることができます
“数と6マイナス7の積”
“7未満”は”マイナス7″を意味し、この場合は”aの積”と記述されている量に対して”マイナス7″を意味します。数および6″。 代数式における数学フレーズの最終的な解釈は次のとおりです。
6k-7
例4:数学フレーズ”数と4の平均”の代数式を記述します。,
解決策:この特定の数学のフレーズを始めるには、”平均”という言葉が何を意味するのかを確認する必要があります。 二つ以上の数字の平均または平均を計算するには、合計を得るためにすべての数字を合計し、それをエントリの数または数が何個あるかで割る必要 Mを未知の数を表す変数とすると、上記の数学フレーズは代数式で表すことができます。
\LARGE{{m+4}\over2}
例5:数学フレーズ”1の商、および1が数だけ減少した”の代数式を書く。,
ソリューション:キーワード”商”は、我々が分割することを意味します。 この場合、数1を数だけ減少した量1で割りたいと思います。 以下は、上記の数学のフレーズを表すことができる代数式です。 Aを未知の数とする。
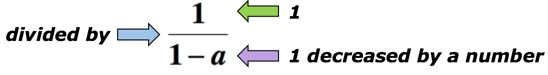
例6:数学フレーズ”2増加した数の平方の三分の一”の代数式を記述します。
解決策:ここでいくつかのことが起こっています。, まず、”数の正方形の三分の一”を述べるフレーズの部分は、”数の正方形を3で割ったもの”と解釈することができます。 未知の数を2で上げてから3で割る必要があります。 未知の数がtであると仮定すると、
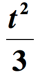
まだ完了していません。 最後のステップは、上記の数量を2で追加して、”2で増加”というフレーズの残りの部分を組み込むことです。 だからここで与えられた数学のフレーズの最終的な表現です。,
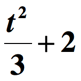
You might also be interested in:
Algebraic Expressions
Algebraic Sentences Word Problems