a sugár és az átmérő után a kör másik fontos része egy ív. Ebben a cikkben részletesen megvitatjuk, hogy mi az ív, hogyan lehet megtalálni az ív hosszát, valamint az ívhossz mérését a radiánokban. A kisebb ívről és a nagyobb ívről is fogunk tanulni.
mi a kör íve?
egy kör íve a kör kerületének bármely része. Emlékeztetni kell arra, hogy egy kör kerülete a kör kerülete vagy távolsága., Ezért azt mondhatjuk, hogy egy kör kerülete maga a kör teljes íve.
hogyan lehet megtalálni az ív hosszát?
az ív kiszámításának képlete azt állítja, hogy:
ívhossz = 2NR (θ/360)
ahol, r = a kör sugara,
π = pi = 3,14
θ = a kör közepén egy ív által részesített szög (fokban).
360 = egy teljes forgatás szöge.
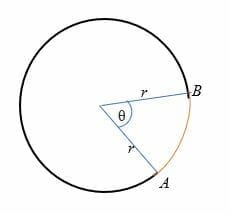
a fenti ábrán látható, hogy az ív hossza (pirossal rajzolva) az a ponttól a B pontig terjedő távolság.,
dolgozzunk ki néhány példa problémát az ív hosszával kapcsolatban:
példa 1
tekintettel arra, hogy az ív AB 40 fokos szöget részesít egy kör középpontjához, amelynek sugara 7 cm. Számítsa ki az AB ív hosszát.
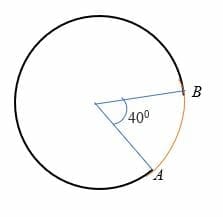
= 7 cm
θ = 40 fok.
helyettesítéssel,
az ív hossza = 2NR(θ/360)
Hossz = 2 x 3.14 x 7 x 40/360
= 4.884 cm.
2. példa
keresse meg egy kör ívének hosszát, amely 120 fokos szöget részesít egy kör középpontjához, amelynek sugara 24 cm.,
az ív hossza = 2NR (θ/360)
= 2 x 3,14 x 24 x 120/360
= 50,24 cm.
példa 3
az ív hossza 35 m. ha a kör sugara 14 m, keresse meg az ív által részesített szöget.
az ív hossza = 2NR(θ/360)
35 m = 2 x 3,14 x 14 x (θ/360)
35 = 87,92 θ/360
mindkét oldalt szorozzuk meg 360-mal a frakció eltávolításához.
12600 = 87,92 θ
osztja mindkét oldalt 87,92
θ = 143,3 fokkal.,
4. példa
keresse meg a 156 cm hosszú ív sugarát, és a kör középpontjához 150 fokos szöget zárjon be.
az ív hossza = 2NR(θ/360)
156 cm = 2 x 3.14 x R x 150/360
156 = 2.6167 r
mindkét oldalt 2.6167
r = 59.62 cm.
tehát az ív sugara 59,62 cm.
hogyan lehet megtalálni az ívhosszt a Radiánokban?
összefüggés van a radián ívben részesített szöge és az ív hosszának a kör sugarához viszonyított aránya között., Ebben az esetben
θ = (az ív hossza) / (a kör sugara).
ezért a radianokban az ív hosszát a
S = r θ
ahol, θ = a szöget a radianokban
S = az ív hossza adja meg.
r = a kör sugara.
az egyik radián a központi szög, amelyet egy sugár ívhossza részez, azaz s = r
a radián csak egy másik módja a szög méretének mérésére. Például, ha a szögeket fokról radiánra konvertáljuk, szorozzuk meg a szöget (fokban) π/180-mal.,
Hasonlóképpen, a radiánok fokokká alakításához szorozzuk meg a szöget (radiánban) 180/π
5.példa
keresse meg egy ív hosszát, amelynek sugara 10 cm, a szög pedig 0, 349 radián.
ívhossz = r θ
= 0,349 x 10
= 3,49 cm.
6. példa
keresse meg a radianokban egy ív hosszát, amelynek sugara 10 m, szöge pedig 2, 356 radián.
ívhossz = r θ
= 10 m x 2.356
= 23.56 m.
7. példa
keresse meg a 10.05 mm hosszúságú és 8 mm sugarú ív által részesített szöget.,
ívhossz = r θ
10,05 = 8 θ
Oszd meg mindkét oldalt 8-mal.
1.2567 = θ
ott az ív által részesített szög 1.2567 radián.
8. példa
Számítsa ki egy olyan kör sugarát, amelynek ívhossza 144 méter, ívszöge pedig 3,665 radián.
ívhossz = r θ
144 = 3,665 r
Oszd meg mindkét oldalt 3,665-tel.
144/3. 665 = r
r = 39,29 yard.
9. példa
Számítsa ki egy ív hosszát, amely 6, 283 radián szöget részesít egy 28 cm sugarú kör középpontjába.,
ívhossz = r θ
= 28 x 6.283
= 175.93 cm
kisebb ív (h3)
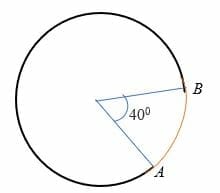
a kisebb ív olyan ív, amely kevesebb, mint 180 fokos szöget részesít a kör középpontjához. Más szavakkal, a kisebb ív kisebb, mint egy félkör, amelyet a körön két pont képvisel. Például az alábbi körben az AB ív a kisebb ív.
Major arc (h3)
a kör fő íve egy olyan ív, amely több mint 180 fokos szöget részesít a kör középpontjához., A fő ív nagyobb, mint a félkör, amelyet egy kör három pontja képvisel.
például a PQR az alábbi kör fő íve. 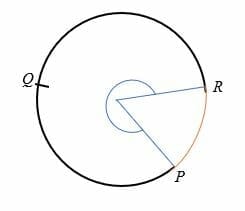
Gyakorlat Problémák
- keresse meg a területet a szektorban a kör sugara 9 mm-es. Feltételezem, hogy a szög subtended ez arc a központban, 30 o.
- Város Egy van Északra, a város B. A szélességi, a város, illetve a város B 54 o N 45 o N ill. Mi az észak-déli távolság a két város között? A Föld sugara 6400 km.,