ei ole Olemassa yhtä strategiaa kääntämiseen matematiikan lauseita algebralausekkeissa. Niin kauan kuin muistaa perusasiat, pitäisi pystyä tarttumaan haastavampiin. Varmista vain, että voit perustella, miten keksit oman algebrallisen ilmaisun, ja mikä tärkeintä, että se on järkevää sinulle. Pyydä aina tarvittaessa apua opettajiltasi tai tee yhteistyötä luokkatovereidesi kanssa, jotta voit varmistaa vastauksesi.,
rakentaa taitojasi kirjallisesti algebralausekkeissa, me mennä yli eri tapoja, miten kukin toiminta voi näkyä sana tai lause ongelma. Mukana olevat neljä aritmeettista operaatiota ovat yhteenlasku,vähennyslasku, kertolasku ja jako.,
Key Words for Addition

Key Words for Subtraction

Key Words for Multiplication

Key Words for Division

It is time now time to go over some examples to practice writing algebraic expressions., En erota esimerkkejä kahteen:
- Perus esimerkkejä algebrallinen ilmaukset
- Multi-osa esimerkkejä algebrallinen ilmaukset
Algebrallisia Lausekkeita Esimerkkejä
Esimerkki 1: Kirjoita lausekkeella math lause ”summa numero ja neljä”.
ratkaisu: sana ”summa” antaa heti vihjeen, että lisäämme tähän. Huomaa, että haluamme lisätä kaksi määrää: yksi tuntematon numero ja numero 4. Koska emme tiedä numeron arvoa, voimme käyttää muuttujaa sen edustamiseen., Voit käyttää mitä tahansa aakkosia. Tässä tapauksessa, sovitaan käyttää y muuttuja.
kun lisäämme muuttujan y ja 4, meillä on y + 4. On myös OK kirjoittaa vastauksesi 4 + y: ksi, koska lisäys on kommutatiivinen – eli lisäjärjestyksen vaihtaminen ei muuta sen summaa.
lopullinen vastaus on y+4.
Esimerkki 2: Kirjoita lausekkeella math lause ”10 kasvoi useita”.
ratkaisu: avainsanat ”lisääntynyt” merkitsevät lisäystä. Tämä tarkoittaa, että 10: een on lisätty tuntematon numero., Käyttämällä kirjain k muuttuja, voimme kääntää lausuman edellä 10 + k. koska lisäys on kommutatiivinen, voimme kirjoittaa sen k + 10. Jompikumpi edellä mainituista on oikea vastaus.
lopullinen vastaus on k+10.
Esimerkki 3: Kirjoita lausekkeella math lause ”ero 1 ja numero”.
Ratkaisu: sana ”ero” viittaa siihen, että aiomme vähentää. Lisäksi, kun kohtaat tämän matematiikan sana (ero) muista kiinnittää huomiota järjestyksessä. Numero 1 tulee ensin, sitten tuntematon numero tulee toiseksi., Se tarkoittaa, että numero 1 on minuend ja tuntematon numero on subtrahend. Jos päätämme käyttää x-kirjain kuin meidän muuttuja, vastaus tulee 1 − x.
lopullinen vastaus on 1 – x.
Esimerkki 4: Kirjoita lausekkeella math lause ”määrä vähemmän kuin 8”.
ratkaisu: ole hyvin varovainen, kun käsittelet avainsanoja ”vähemmän kuin”. Ensimmäinen määrä, joka tulee ennen ”vähemmän kuin” avainsanat, joka on ”useita” on subtrahend. Kun taas määrä, joka tulee sen jälkeen tulee minuend.,
eli aiomme vähentää tuntemattoman luvun numerosta 8. Jos me valitsemme muuttuja on kirjain, saamme 8−.
lopullinen vastaus on 8 -.
Esimerkki 5: Kirjoita lausekkeella math lause ”tuote 5 ja numero”.
ratkaisu: kahden määrän tai arvon tuotteen löytäminen tarkoittaa sitä, että moninkertaistamme ne yhdessä. Valitsemalla m-kirjain kuin meidän muuttuja, algebrallinen lauseke tämä matematiikka lause on vain 5m. Se tarkoittaa 5 kertaa tuntematon numero m.
lopullinen vastaus on 5m.,
Esimerkki 6: Kirjoita lausekkeella math lause ”kaksi kertaa numero”.
ratkaisu: Sana ”Kahdesti” tarkoittaa, että aiomme tuplata jotain. Tässä tapauksessa haluamme kaksinkertaistaa tuntemattoman arvon tai määrän. Anna kirjain d on tuntematon numero, kun meidän kahden hengen me saamme algebrallinen lauseke 2d.
lopullinen vastaus on 2d.
Esimerkki 7: Kirjoita lausekkeella math lause ”osamäärä numero ja 7”.
ratkaisu: avainsana ”osamäärä” tarkoittaa, että suoritamme jakautumisen toimintaa. Jaamme tuntemattoman luvun 7., Valitsemalla kirjain w meidän muuttuja, matematiikka lause edellä voidaan ilmaista algebrallinen lauseke alla.
\LARGE{w \yli 7}
Esimerkki 8: Kirjoita lausekkeella math lause ”suhde 10 ja numero”.
ratkaisu: vastaavasti sana ”suhde” tarkoittaa jakoa. Järjestys täällä on hyvin tärkeä. Ensimmäinen määrä on numero 10 ja toinen määrä tuntematon numero. Se tarkoittaa, että 10 jaetaan tuntemattomalla numerolla., Olkoon c on tuntematon numero, algebrallinen lauseke matematiikka lause edellä voidaan kirjoittaa
\LARGE{10 \over c}
Multi-Osa algebralausekkeissa Esimerkkejä
Tällä kertaa, meidän tulee käsitellä matemaattisia lauseita, jotka ovat hieman monimutkaisempia. Algebralliset lausekkeet voivat sisältää kaksi tai useampia operaatioita. Perus avainsanat, että opimme ennen toimii perustana työstämme haastavampia matematiikan lauseita tulkita osaksi algebraic ilmaisuja.,
Esimerkki 1: Kirjoita lausekkeella math lause ”3 enemmän kuin kaksi kertaa numero”.
ratkaisu: jotta tämä olisi paljon helpompi ymmärtää, aiomme jakaa tämän lauseen kahteen osaan. Ensinnäkin, tunnista, että meillä on tuntematon numero. Voimme edustaa sitä millä tahansa aakkosten kirjaimilla. Olkoon tuntematon numero muuttuja x. alla olevan kaavion pitäisi auttaa meitä näkemään, mitä todella tapahtuu.,
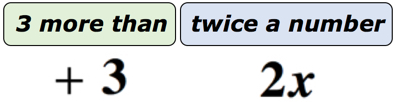
Jos ajattelee sitä, on tuntematon numero edustaa muuttuja x, joka on kaksinkertaistunut tai kerrottuna 2. Mikä tahansa on tuote, lisäämme siihen 3. Lopullisen vastauksemme pitäisi näyttää alla olevalta.
lopullinen vastaus on 2x+3.
Esimerkki 2: Kirjoita lausekkeella math lause ”ero puolen numero ja 10”.
ratkaisu: oletetaan muuttujan y olevan tuntematon numero., Avainsana ” ero ” kehottaa meitä, että aiomme suorittaa vähennyslasku. Tässä yhteydessä on ratkaisevan tärkeää kiinnittää huomiota vähennysjärjestykseen. Sanan ” ero ” jälkeen pitäisi odottaa kaksi määrää. Ensimmäinen on minuend, toinen taas subtrahend. Katso alla oleva kaavio.
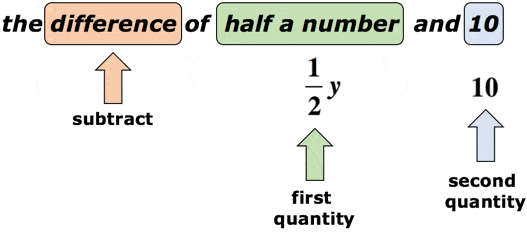
Viitaten kaavio edellä, me vähennämme ensimmäinen määrä toisen määrä. Toisin sanoen toinen määrä vähennetään ensimmäisestä määrästä., Lopullinen vastaus math lause olisi jotain tällaista,
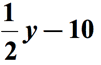
Esimerkki 3: Kirjoita lausekkeella math lause ”7 vähemmän kuin tuote numero ja 6”.
Ratkaisu: tiedämme, että ”vähemmän kuin”, ehdottaa vähennyslaskua toimintaa. Mutta meidän täytyy olla hieman varovaisia täällä, koska järjestys siitä, miten vähennämme on tärkeää. Oletetaan, että tuntematon numero edustaa muuttujaa k. laitetaan tämä kaavioon, jotta siinä olisi järkeä.,
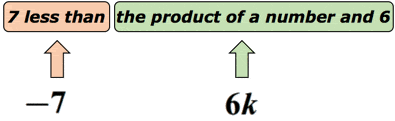
Itse asiassa, tämä matematiikka lause voidaan kirjoittaa muotoon
” tuote numero ja 6, miinus 7 ”
”7 vähemmän kuin” tarkoittaa ”miinus 7” mitä määrä on kuvattu, joka tässä tapauksessa ”tuote numero ja 6”. Tässä on lopullinen tulkinta matematiikan lause on algebrallinen lauseke:
6k-7
Esimerkki 4: Kirjoita lausekkeella math lause ”keskimäärin useita ja 4”.,
ratkaisu: päästäksemme alkuun tässä nimenomaisessa matemaattisessa lauseessa, meidän täytyy tarkistaa, mitä sana ”keskiarvo” tarkoittaa. Laskea keskiarvo tai keskiarvo kahden tai useamman numeroita, meidän täytyy lisätä jopa kaikki numerot saada summa, sitten jakaa sen määrä merkintöjä tai kuinka monta numerot on. Jos emme anna m muuttuja edustaa tuntematon numero, matematiikka lause yllä voidaan ilmaista algebrallinen ilmaukset kuten,
\LARGE{{m + 4} \over 2}
Esimerkki 5: Kirjoita lausekkeella math lause ”osamäärä 1, ja 1 laski numero”.,
ratkaisu: avainsana ”osamäärä” tarkoittaa, että jaamme. Tässä tapauksessa haluamme jakaa luvun 1 määrällä 1 vähennettynä luvulla. Alla on algebrallinen lauseke, joka voi edustaa yllä olevaa matemaattista lausetta. Olkoon a tuntematon numero.
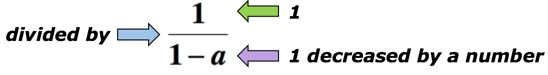
Esimerkki 6: Kirjoita lausekkeella math lause ”kolmannen neliön numero, kasvoi 2”.
ratkaisu: tässä on muutama asia menossa., Ensimmäinen osa lause, jossa todetaan, ”kolmannen neliön numero” voidaan tulkita ” neliön määrä jaettuna 3 ”. Meidän täytyy nostaa tuntematon numero 2 sitten jakaa 3. Oletetaan, että tuntematon numero on t, saamme
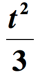
– Emme ole tehneet vielä. Viimeinen vaihe on lisätä määrä edellä 2 sisällyttää jäljellä oleva osa lause ”kasvoi 2”. Tässä on viimeinen esitys annetusta matemaattisesta lauseesta.,
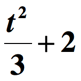
You might also be interested in:
Algebraic Expressions
Algebraic Sentences Word Problems