Der er ingen enkelt strategi for at oversætte matematiske sætninger til algebraiske udtryk. Så længe du kan huske det grundlæggende, skal du være i stand til at tackle de mere udfordrende. Bare sørg for at du kan retfærdiggøre, hvordan du kommer op med dit eget algebraiske udtryk, og endnu vigtigere, at det giver mening for dig. Bed altid om hjælp fra dine lærere, efter behov eller samarbejd med dine klassekammerater, så du kan bekræfte dine svar.,
for at opbygge dine færdigheder i at skrive algebraiske udtryk, vil vi gå over forskellige måder, hvordan hver operation kan dukke op som et ord eller en sætning i problemet. De fire aritmetiske operationer involveret er addition, subtraktion, multiplikation og division.,
Key Words for Addition

Key Words for Subtraction

Key Words for Multiplication

Key Words for Division

It is time now time to go over some examples to practice writing algebraic expressions., Jeg adskille eksempler i to:
- Grundlæggende eksempler af algebraiske udtryk
- Multi-en del eksempler af algebraiske udtryk
Grundlæggende Algebraiske Udtryk Eksempler
Eksempel 1: Skriv et algebraisk udtryk for den matematiske sætning “det er summen af en række og fire”.
løsning: ordet “sum” giver os straks det tip, som vi vil tilføje her. Bemærk, at vi vil tilføje to mængder: et ukendt nummer og nummer 4. Da vi ikke ved, hvad værdien af nummeret er, kan vi bruge en variabel til at repræsentere den., Du kan bruge alle bogstaver i alfabetet. Lad os i dette tilfælde acceptere at bruge y til variablen.
Når vi tilføjer variablen y og 4, har vi y + 4. Det er også okay at skrive dit svar som 4 + y, fordi tilføjelse er kommutativ – det vil sige at skifte rækkefølgen af tilføjelse ændrer ikke summen.
det endelige svar er y+4.eksempel 2: Skriv et algebraisk udtryk for matematikfrasen “10 øget med et tal”.
løsning: nøgleordene “øget med” indebærer tilføjelse. Det betyder, at et ukendt nummer er blevet tilføjet til 10., Ved hjælp af bogstavet k som variablen kan vi oversætte sætningen ovenfor som 10 + k. da tilføjelsen er kommutativ, kan vi omskrive den som K + 10. En af de to ovenfor er et korrekt svar.
det endelige svar er K+10.eksempel 3: Skriv et algebraisk udtryk for matematikfrasen”forskellen på 1 og et tal”.
løsning: ordet “forskel” antyder, at vi vil trække fra. Når du støder på dette matematiske ord (forskel), skal du desuden være opmærksom på ordren. Nummeret 1 kommer først, så kommer et ukendt nummer på andenpladsen., Det betyder, at tallet 1 er minuenden, og det ukendte nummer er subtrahenden. Hvis vi beslutter at bruge bogstavet as som vores variabel, bliver svaret 1 -..
det endelige svar er 1 -..
eksempel 4: Skriv et algebraisk udtryk for matematikfrasen “et tal mindre end 8”.
løsning: vær meget forsigtig, når du beskæftiger dig med nøgleordene “mindre end”. Den første mængde, der kommer før de “mindre end” søgeord, som er “et tal” er subtrahend. Mens den mængde, der kommer efter det bliver minuend.,
med andre ord vil vi trække det ukendte nummer fra tallet 8. Hvis vi vælger vores variabel til at være bogstavet a, får vi 8 − a.
det endelige svar er 8 – a.
eksempel 5: Skriv et algebraisk udtryk for matematikfrasen “produktet af 5 og et tal”.
løsning: for at finde produktet af to mængder eller værdier betyder det, at vi vil formere dem sammen. Hvis du vælger bogstavet m som vores variabel, er det algebraiske udtryk for denne matematiske sætning simpelthen 5m. det betyder 5 gange det ukendte nummer m.
det endelige svar er 5m.,eksempel 6: Skriv et algebraisk udtryk for matematikfrasen”to gange et tal”.
løsning: ordet “to gange” betyder, at vi vil fordoble noget. I dette tilfælde ønsker vi at fordoble en ukendt værdi eller mængde. Lad bogstavet d være ukendt nummer, når vi fordoble det, at vi får den algebraiske udtryk 2d.
Det endelige svar er 2d.
Eksempel 7: Skriv et algebraisk udtryk for den matematiske sætning “kvotienten af et nummer, og 7”.
løsning: nøgleordet “kvotient” betyder, at vi udfører driften af division. Vi deler et ukendt nummer med 7., Hvis du vælger bogstavet as som vores variabel, kan matematikfrasen ovenfor udtrykkes som det algebraiske udtryk nedenfor.
\LARGE {\\over 7}
Eksempel 8: Skriv et algebraisk udtryk for matematikfrasen “forholdet mellem 10 og et tal”.
løsning: tilsvarende betyder ordet “forhold” division. Ordren her er meget vigtig. Den første mængde er nummer 10, og den anden mængde er det ukendte nummer. Det betyder, at 10 er divideret med et ukendt nummer., Lad c være ukendt nummer, algebraisk udtryk for den matematiske sætning ovenfor kan skrives som
\LARGE{10 \over c}
Multi-Del Algebraiske Udtryk Eksempler
Denne gang, vi vil beskæftige sig med matematiske sætninger, som er en smule mere kompleks. De algebraiske udtryk her kan indeholde to eller flere operationer. De grundlæggende søgeord, som vi lærer før, vil fungere som fundamentet, når vi arbejder med de mere udfordrende matematiske sætninger til at fortolke til algebraiske udtryk.,
Eksempel 1: Skriv et algebraisk udtryk for den matematiske sætning “3 mere end to gange et tal”.
løsning: for at gøre dette meget lettere at forstå, vil vi opdele denne sætning i to dele. Først skal du erkende, at vi har et ukendt nummer. Vi kan repræsentere det ved alle bogstaver i alfabetet. Lad det ukendte nummer være variablen.. diagrammet nedenfor skal hjælpe os med at se, hvad der virkelig foregår.,
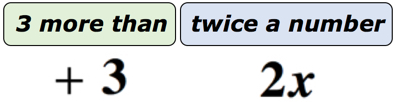
Hvis du tænker over det, er der et ukendt antal er repræsenteret ved variabel x, der er ved at blive fordoblet eller ganges med 2. Uanset hvad der er produktet, vil vi tilføje 3 til det. Så vores endelige svar skal se ud som det nedenfor.
det endelige svar er 2.+3.eksempel 2: Skriv et algebraisk udtryk for matematikfrasen”forskellen på et halvt tal og 10″.
løsning: Antag, at variablen y er det ukendte nummer., Nøgleordet” forskel ” beder os om, at vi skal udføre subtraktion. Det er afgørende her, at vi er opmærksomme på rækkefølgen af subtraktion. Efter ordet” forskel ” bør vi forvente to mængder. Den første bliver minuenden, mens den anden bliver subtrahend. Tag et kig på diagrammet nedenfor.
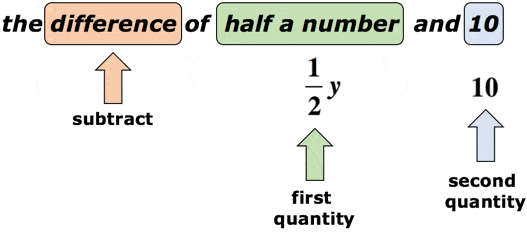
med Henvisning til ovenstående diagram, vi vil trække den første mængde af den anden mængde. Med andre ord trækkes den anden mængde fra den første mængde., Det endelige svar til matematik en sætning, gerne noget som dette,
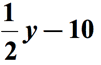
Eksempel 3: Skriv et algebraisk udtryk for den matematiske sætning “7 mindre end et produkt af et tal og 6”.
løsning: vi ved, at “mindre end” antyder en subtraktionsoperation. Men vi skal være lidt forsigtige her, fordi ordren om, hvordan vi trækker fra, er vigtig. Antag, at det ukendte nummer er repræsenteret af variablen k. lad os sætte dette på et diagram for at få en fornemmelse af det.,
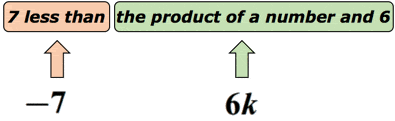
Faktisk, dette regnestykke kan skrives som
” et produkt af et tal og 6 minus 7 “
“7 mindre end” betyder “minus 7” til hvilken som helst mængde, der bliver beskrevet, som i dette tilfælde er “et produkt af et tal og 6”. Her er den endelige fortolkning af de matematiske sætning i et algebraisk udtryk:
6k-7
Eksempel 4: Skriv et algebraisk udtryk for den matematiske sætning “gennemsnittet af en række og 4”.,
løsning: for at komme i gang med denne særlige matematiske sætning skal vi gennemgå, hvad ordet “gennemsnit” betyder. For at beregne gennemsnittet eller gennemsnittet af to eller flere tal skal vi tilføje alle tallene for at få et beløb og derefter dele det med antallet af poster eller hvor mange tal der er. Hvis vi lad m være den variabel, der repræsenterer det ukendte tal, matematik ovenstående sætning kan udtrykkes i algebraiske udtryk som,
\LARGE{{m + 4} \over 2}
Eksempel 5: Skriv et algebraisk udtryk for den matematiske sætning “kvotienten mellem 1 og 1 faldt ved et nummer”.,
løsning: nøgleordet “kvotient” betyder, at vi vil opdele. I dette tilfælde ønsker vi at dividere tallet 1 med mængden 1 faldet med et tal. Nedenfor er det algebraiske udtryk, der kan repræsentere matematikfrasen ovenfor. Lad en være det ukendte nummer.
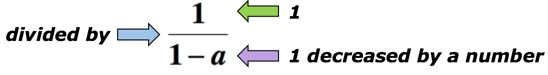
Eksempel 6: Skriv en algebraisk udtryk for den matematiske sætning “en tredjedel af pladsen i en række, steg med 2”.
løsning: der er et par ting der foregår her., For det første kan den del af sætningen, der angiver “en tredjedel af kvadratet af et tal”, fortolkes som ” kvadratet af et tal divideret med 3 “. Vi bliver nødt til at hæve det ukendte nummer med 2 og derefter dividere med 3. Antag, at det ukendte nummer er t, vi får
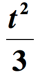
Vi er ikke færdige endnu. Det sidste trin at gøre er at tilføje mængden ovenfor med 2 for at inkorporere den resterende del af udtrykket ” øget med 2 “. Så her er den endelige repræsentation af den givne matematiske sætning.,
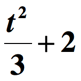
You might also be interested in:
Algebraic Expressions
Algebraic Sentences Word Problems