neexistuje žádná jediná strategie pro překlad matematických frází do algebraických výrazů. Pokud si pamatujete základy, měli byste být schopni řešit ty náročnější. Jen se ujistěte, že můžete ospravedlnit, jak přicházíte s vlastním algebraickým výrazem, a co je důležitější, že vám to dává smysl. Vždy požádejte o pomoc své učitele, podle potřeby nebo Spolupracujte se svými spolužáky, abyste mohli ověřit své odpovědi.,
Chcete-li vytvořit své dovednosti při psaní algebraických výrazů, projdeme různými způsoby, jak se každá operace může ukázat jako slovo nebo fráze v problému. Čtyři aritmetické operace jsou sčítání, odčítání, násobení a dělení.,
Key Words for Addition

Key Words for Subtraction

Key Words for Multiplication

Key Words for Division

It is time now time to go over some examples to practice writing algebraic expressions., Jsem samostatný příklady do dvou:
- Základní příklady algebraické výrazy
- Multi-část příklady algebraické výrazy
Základní Algebraické Výrazy Příklady
Příklad 1: Napište algebraický výraz pro matematický výraz „součet množství a čtyři“.
řešení: slovo “ sum “ nám okamžitě dává náznak, který zde přidáme. Všimněte si, že chceme přidat dvě množství: jedno neznámé číslo a číslo 4. Protože nevíme, jaká je hodnota čísla, můžeme ji reprezentovat pomocí proměnné., Můžete použít všechna písmena abecedy. V tomto případě souhlasíme s použitím Y pro proměnnou.
když přidáme proměnnou y a 4, Máme y + 4. Je také v pořádku napsat odpověď jako 4 + y, protože sčítání je komutativní-to znamená, že přepínání pořadí sčítání nemění jeho součet.
konečná odpověď je y + 4.
příklad 2: Napište algebraický výraz pro matematickou frázi“10 zvýšeno o číslo“.
řešení: klíčová slova „zvýšená o“ znamenají přidání. To znamená, že neznámé číslo bylo přidáno do 10., Pomocí písmene k jako proměnné můžeme výše uvedené prohlášení přeložit jako 10 + k.protože přidání je komutativní, můžeme jej přepsat jako k + 10. Jedna z výše uvedených dvou je správná odpověď.
konečná odpověď je k + 10.
příklad 3: Napište algebraický výraz pro matematickou frázi „rozdíl 1 a číslo“.
řešení: slovo „rozdíl“ naznačuje, že se odečteme. Kromě toho, když narazíte na toto matematické slovo (rozdíl), nezapomeňte věnovat pozornost objednávce. Číslo 1 je na prvním místě a na druhém místě je neznámé číslo., To znamená, že číslo 1 je minuend a neznámé číslo je subtrahend. Pokud se rozhodneme použít písmeno x jako naše proměnná, odpověď se stává 1 − x.
poslední odpověď je 1 – x.
Příklad 4: Napište algebraický výraz pro matematický výraz „menší číslo než 8“.
řešení: buďte velmi opatrní při řešení klíčových slov „méně než“. První množství, které přichází před klíčová slova“ méně než“, což je“ číslo“, je subtrahend. Zatímco množství, které přichází poté, co se stane minuend.,
jinými slovy odečteme neznámé číslo od čísla 8. Pokud zvolíme naši proměnnou jako písmeno a, dostaneme 8 – a.
konečná odpověď je 8-a.
příklad 5: napište algebraický výraz pro matematickou frázi „produkt 5 a číslo“.
Řešení: Chcete-li najít produkt dvou veličin nebo hodnot, znamená to, že je vynásobíme dohromady. Výběr písmeno m jako naše proměnná, algebraický výraz pro tento matematický výraz je jednoduše 5m. To znamená 5 krát neznámé číslo m.
poslední odpověď je 5m.,
příklad 6: Napište algebraický výraz pro matematickou frázi „dvakrát za číslo“.
řešení: slovo „dvakrát“ znamená, že něco zdvojnásobíme. V tomto případě chceme zdvojnásobit neznámou hodnotu nebo množství. Nechť písmeno d bylo to neznámé číslo, když ho zdvojnásobíme, dostaneme algebraické vyjádření 2d.
poslední odpověď je 2d.
Příklad 7: Napište algebraický výraz pro matematický výraz „kvocient řady a 7“.
řešení: Klíčové slovo „kvocient“ znamená, že provádíme operaci dělení. Neznámé číslo rozdělíme na 7., Při výběru písmene w jako naší proměnné lze výše uvedenou matematickou frázi vyjádřit jako algebraický výraz níže.
\LARGE{w \over 7}
příklad 8: napište algebraický výraz pro matematickou frázi „poměr 10 a číslo“.
řešení: podobně slovo „poměr“ znamená rozdělení. Pořadí je zde velmi důležité. První množství je číslo 10 a druhé množství je neznámé číslo. To znamená, že 10 je děleno neznámým číslem., Nechť c je neznámé číslo, algebraický výraz pro matematiku frázi výše lze zapsat jako
\LARGE{10 \over c}
Multi-Část Algebraické Výrazy Příklady
Tento čas, budeme řešit matematické věty, které jsou trochu složitější. Algebraické výrazy zde mohou obsahovat dvě nebo více operací. Základní klíčová slova, která se budeme učit, než bude sloužit jako základ, jak budeme pracovat s náročnější matematické věty interpretovat do algebraických výrazů.,
Příklad 1: Napište algebraický výraz pro matematickou frázi „3 více než dvakrát za číslo“.
řešení: abychom to mnohem lépe pochopili, rozdělíme tuto frázi na dvě části. Nejprve si uvědomte, že máme neznámé číslo. Můžeme ji reprezentovat libovolnými písmeny abecedy. Nechť neznámé číslo je proměnná x. níže uvedený diagram by nám měl pomoci zjistit, co se skutečně děje.,
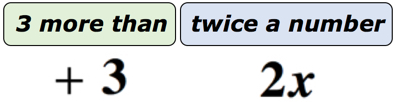
Pokud si myslíte o tom, že je neznámé číslo reprezentované proměnnou x, která je zdvojené či násobené 2. Ať už je produkt jakýkoli, přidáme k němu 3. Takže naše konečná odpověď by měla vypadat jako ta níže.
konečná odpověď je 2x + 3.
příklad 2: Napište algebraický výraz pro matematickou frázi „rozdíl půl čísla a 10“.
řešení: Předpokládejme, že proměnná y je neznámé číslo., Klíčové slovo „rozdíl“ nás vyzývá, abychom provedli odčítání. Zde je velmi důležité věnovat pozornost pořadí odčítání. Po slově „rozdíl“ bychom měli očekávat dvě množství. První z nich bude minuend, zatímco druhý bude subtrahend. Podívejte se na níže uvedený diagram.
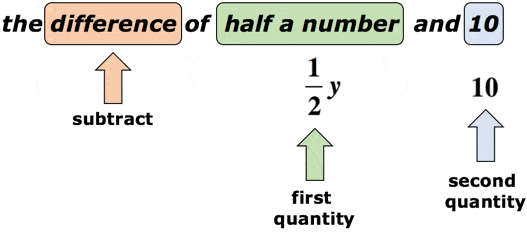
s Odkazem na diagram výše, budeme odečíst první veličina druhá veličina. Jinými slovy, druhé množství se odečte od prvního množství., Konečná odpověď na matematický výraz, jako by něco takového,
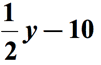
Příklad 3: Napište algebraický výraz pro matematický výraz „7 méně než výrobek z řady a 6“.
řešení: víme, že“ méně než “ naznačuje odčítání. Ale musíme být trochu opatrní, protože pořadí, jak odečteme, je důležité. Předpokládejme, že neznámé číslo je reprezentováno proměnnou k.dáme to na diagram, abychom to pochopili.,
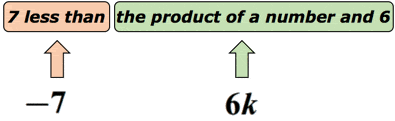
ve Skutečnosti, tento matematický výraz může být přepsán jako
“ produkt z řady a 6 mínus 7 „
„7 méně než“ znamená „mínus 7“ na cokoliv, co množství je popsáno, který je v tomto případě „produkt z řady a 6“. Zde je konečný výklad matematický výraz v algebraického výrazu:
6k-7
Příklad 4: Napište algebraický výraz pro matematický výraz „průměrná čísla a 4“.,
řešení: abychom mohli začít s touto konkrétní matematickou frází, musíme zkontrolovat, co znamená slovo „průměr“. Vypočítat průměr nebo průměr dvou nebo více čísel, musíme sečíst všechna čísla získat částku vydělíte počet položek nebo kolik jich existuje. Pokud bychom nechť m je proměnná reprezentovat neznámé číslo, matematika frázi výše může být vyjádřena v algebraické výrazy jako,
\LARGE{{m + 4} \over 2}
Příklad 5: Napište algebraický výraz pro matematický výraz „kvocient 1, a 1 snížená řada“.,
řešení: Klíčové slovo „kvocient“ znamená, že se rozdělíme. V tomto případě chceme rozdělit číslo 1 o množství 1 snížené o číslo. Níže je algebraický výraz, který může představovat matematickou frázi výše. Nechť a je neznámé číslo.
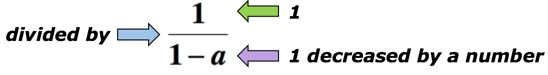
Příklad 6: Napište algebraický výraz pro matematický výraz „třetí náměstí číslo, se zvýšil o 2“.
řešení: zde se děje několik věcí., Za prvé, část fráze, která uvádí „třetinu čtverce čísla“, může být interpretována jako „čtverec čísla děleného 3“. Budeme muset zvýšit neznámé číslo o 2 a pak rozdělit o 3. Předpokládejme, že neznámé číslo je t, dostaneme
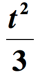
my Jsme to ještě neudělali. Posledním krokem je přidání výše uvedeného množství o 2, aby se začlenila zbývající část fráze „zvýšená o 2“. Takže tady je konečné znázornění dané matematické fráze.,
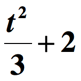
You might also be interested in:
Algebraic Expressions
Algebraic Sentences Word Problems