Să presupunem că doriți să luați în considerare impactul unui factor de risc asupra timpului până la apariția unui eveniment. De exemplu, Arnlov et al (2010) ia în considerare impactul indicelui de masă corporală (IMC) și al sindromului metabolic asupra dezvoltării bolilor cardiovasculare și a decesului la bărbații de vârstă mijlocie. Asociațiile au fost investigate folosind date dintr-un studiu de cohortă a bărbaților suedezi de vârstă mijlocie 1758 care locuiesc într-un județ cu peste 30 ani de urmărire., Figura de mai jos descrie timpul până la un eveniment cardiovascular major în funcție de categoria IMC și prezența (B) sau absența (a) sindromului metabolic. Există o diferență în aceste curbe de supraviețuire?
Figura 2: curbele Kaplan-Meier pentru evenimente cardiovasculare majore în diferite categorii de IMC la persoanele fără MetS (A) și cu MetS (B).
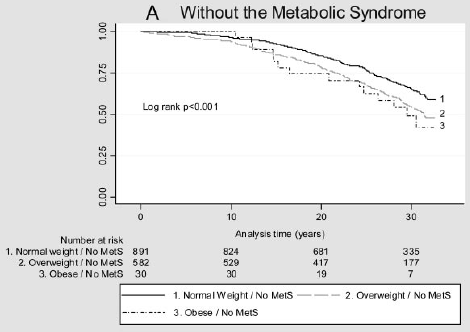
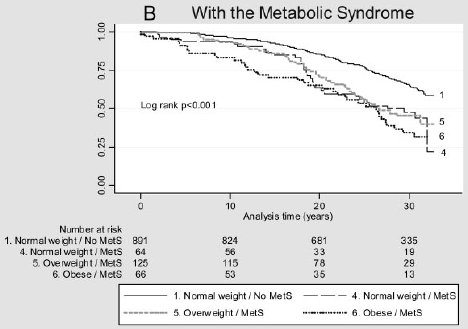
(Figurile reproduse din Arnlov, J et al., Impactul indicelui de masă corporală și a sindromului Metabolic asupra riscului de boli cardiovasculare și deces la bărbații de vârstă mijlocie. Circulație 2010; 121; 230-236, publicat inițial on-line 12/28/2009; DOI 10.1161/CIRCULATIONAHA.Apariția unui eveniment cardiovascular major este un răspuns binar. Ar fi adecvată regresia logistică, cu IMC ca variabilă predictor, pentru a analiza aceste date?,
răspuns
relația dintre prezența sau absența unui eveniment cardiovascular major și variabila predictor ar putea fi evaluată cu regresie logistică la un moment dat, dar acest lucru nu ar compara direct curbele de supraviețuire. O analiză de supraviețuire ar compara curbele pe baza timpului cu evenimentul.metodele de analiză a supraviețuirii, cum ar fi regresia proporțională a pericolelor, diferă de regresia logistică prin evaluarea unei rate în loc de o proporție.,
\(\lambda \left ( t|x_{1i},X_{2i},…,X_{ki} \dreapta ) = \ lambda_{0} (t)exp\stânga (\beta_{1}x_{1i}+\beta_{2}x_{2i}+…,+\beta_{K}X_{Ki} \right )\)
Deși nici un anumit model de probabilitate este selectat pentru a reprezenta timpul de supravietuire, de regresie proporțională a riscurilor are o presupunere importantă: pericol pentru orice individ este un procent fix de pericol pentru orice alt individ. (adică pericole proporționale)., Observați dacă \(\lambda_0 (t)\) este funcția de pericol pentru un subiect cu toate predictor valori egale cu zero și \(\lambda_1 (t)\) este funcția de pericol pentru un subiect cu alte valori pentru variabilele predictor, atunci raportul de risc depinde doar de variabilele predictor și nu la momentul t. Această ipoteză înseamnă că, dacă un covariate dubleaza riscul de eveniment pe zi, este, de asemenea, dubleaza riscul de eveniment în orice altă zi.,modelele de risc proporțional pot fi utilizate pentru măsuri discrete sau continue ale timpului evenimentului și pot încorpora covariatele dependente de timp (covariatele ale căror valori se pot schimba în timpul perioadei de observație). Folosind regresia proporțională a pericolelor, se pot produce rapoarte de risc (sau risc) ajustate covariate.să revenim la întrebarea inițială pusă de Arnlov și colleagues…do IMC și sindromul metabolic afectează dezvoltarea bolilor cardiovasculare? Citiți Arnlov și colab., Impactul indicelui de masă corporală și a sindromului Metabolic asupra riscului de boli cardiovasculare și deces în circulația bărbaților de vârstă mijlocie 2010; 121; 230-236, acordând o atenție deosebită metodelor statistice, rezultatelor și concluziilor.
comparați și contrastați abordarea de regresie proporțională a riscurilor cu o abordare de regresie logistică prin citirea lui Franco și colab. Traiectoriile intrării în sindromul Metabolic:studiul Framingham Heart. Circulație 2009;120; 1943-1950; publicat inițial Online 2 noiembrie 2009; American Heart Association. 7272 Greenville Avenue, Dallas, TX DOI: 10.,1161 / CIRCULATIONAHA.109.855817
De asemenea, puteți compara rezultatele celor două studii. Ambele lucrări sunt în dosarul citirilor pentru săptămâna 14.
(accesat din http://www.oxfordjournals.org/our_journals/tropej/online/ma_chap12.pdf)