Etter radius og diameter, en annen viktig del av en sirkel er en bue. I denne artikkelen vil vi diskutere i detaljer hva en bue er, hvordan å finne lengden av en bue, og målingen av en bue lengde i radianer. Vi vil også studere om mindre arc og store arc.
Hva er en rest av en Sirkel?
En bue av en sirkel er en del av omkretsen av en sirkel. Å hente frem, og omkretsen av en sirkel er omkretsen, eller avstanden rundt en sirkel., Derfor kan vi si at omkretsen av en sirkel er full buen av sirkelen i seg selv.
Hvordan for å Finne Lengden av en Bue?
formelen for beregning arc sier at:
Arc lengde = 2nr (θ/360)
Hvor r = radius i sirkelen,
π = pi = 3.14
θ = vinkelen (i grader) subtended av en bue på midten av sirkelen.
360 = vinkelen til en komplett rotasjon.
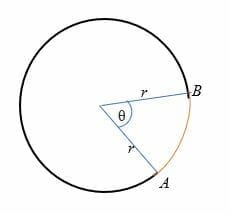
Fra illustrasjonen ovenfor, lengden på arc (trukket i rødt) er avstanden fra punkt A til punkt B.,
La oss jobbe ut et par eksempel problemer om lengden av en bue:
Eksempel 1
Gitt at arc AB subtends en vinkel på 40 grader til midten av en sirkel med radius 7 cm. Beregne lengden av buen AB.
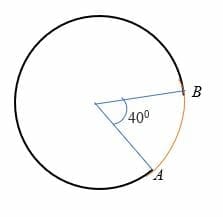
Løsningen
Gitt r = 7 cm
θ = 40 grader.
Ved substitusjon,
lengden av en bue = 2nr(θ/360)
Lengde = 2 x 3.14 x 7 x 40/360
= 4.884 cm.
Eksempel 2
Finne lengden av en bue av en sirkel som subtends en vinkel på 120 grader til midten av en sirkel med radius på 24 cm.,
Løsningen
lengden av en bue = 2nr(θ/360)
= 2 x 3.14 x 24 x 120/360
= 50.24 cm.
Eksempel 3
lengden av en lysbue er 35 meter. Hvis radius i sirkelen er 14 m, finn vinkelen subtended av arc.
Løsningen
lengden av en bue = 2nr(θ/360)
35 m = 2 x 3.14 x 14 x (θ/360)
35 = 87.92 θ/360
Multiplisere begge sider av 360 for å fjerne brøkdel.
12600 = 87.92 θ
Dividere begge sider av 87.92
θ = 143.3 grader.,
Eksempel 4
Finn radien i en bue som er 156 cm i lengde og subtends en vinkel på 150 grader til midten av en sirkel.
Løsningen
lengden av en bue = 2nr(θ/360)
156 cm = 2 x 3.14 x r x 150/360
156 = 2.6167 r
Dividere begge sider av 2.6167
r = 59.62 cm.
Så, radien på buen er 59.62 cm.
Hvordan Finne Arc Lengde i Radianer?
Det er en sammenheng mellom vinkel subtended av en bue i radianer og forholdet mellom lengden av buen til radius i sirkelen., I dette tilfellet,
θ = (lengden av en bue) / (radius i sirkel).
Derfor, lengden av buen i radianer er gitt ved,
S = r θ
der, θ = vinkelen subtended av en bue i radianer
S = lengden av buen.
r = radius i sirkelen.
En radian er det sentrale vinkel subtended av en bue lengden av en radius dvs. s = r
radian er bare en annen måte å måle størrelsen på en vinkel. For eksempel, for å konvertere vinkler fra grader til radianer, må du multiplisere den vinkelen (i grader) ved π/180.,
på samme måte, til å konvertere radianer til grader, må du multiplisere den vinkelen (i radianer) ved 180/π
Eksempel 5
Finne lengden av en bue med radius 10 cm og vinkel subtended er 0.349 radianer.
Løsningen
Arc lengde = r θ
= 0.349 x 10
= 3.49 cm.
Eksempel 6
Finne lengden av en bue i radianer, som har en radius på 10 m og en vinkel på 2.356 radianer.
Løsningen
Arc lengde = r θ
= 10 m x 2.356
= 23.56 m.
Eksempel 7
Finn vinkelen subtended av en bue som har en lengde på 10.05 mm og en radius på 8 mm.,
Løsningen
Arc lengde = r θ
10.05 = 8 θ
Dividere begge sider av 8.
1.2567 = θ
Det kan vinkelen subtended av arc er 1.2567 radianer.
Eksempel 8
Beregne radius i en sirkel der arc lengde er 144 meter og arc vinkel, er 3.665 radianer.
Løsningen
Arc lengde = r θ
144 = 3.665 r
Dividere begge sider av 3.665.
144/3.665 = r
r = 39.29 meter.
Eksempel 9
Beregne lengden av en bue som subtends en vinkel på 6.283 radianer til midten av en sirkel som har en radius på 28 cm.,
Løsningen
Arc lengde = r θ
= 28 x 6.283
= 175.93 cm
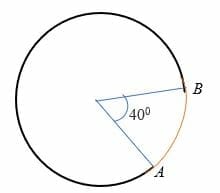
Mindre arc (h3)
mindre arc er en bue som subtends en vinkel på mindre 180 grader til sentrum av sirkelen. Med andre ord, mindre arc mål mindre enn en halvsirkel, og er representert på sirkel med to poeng. For eksempel, arc AB i sirkelen nedenfor er mindre arc.
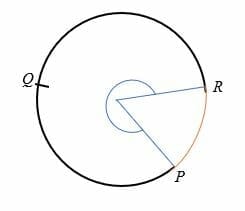
Store arc (h3)
De store arc av en sirkel er en bue som subtends en vinkel på mer enn 180 grader til sentrum av sirkelen., Den store lysbuen er større enn semi – sirkel og er representert med tre poeng på en sirkel.
For eksempel, PQR er den store buen av sirkelen som vises nedenfor.
Praksis Problemer
- Finn arealet av den delen av sirkelen med radius på 9 mm. Anta vinkelen subtended av dette arc i sentrum er 30 o.
- Byen er på grunn Nord for byen B. breddegrader over byen og En by B er 54 o N og 45 o N hhv. Hva er Nord-Sør-avstanden mellom to byer? Radius av Jorden er 6400 km.,