半径と直径の後に、円のもう一つの重要な部分は円弧です。 この記事では、円弧とは何か、円弧の長さを見つける方法、および円弧の長さをラジアン単位で測定する方法について詳細に説明します。 マイナーアークとメジャーアークについても勉強します。
円の円弧とは何ですか?
円の円弧は、円の円周の任意の部分です。 思い出すために、円の円周は、円の周りの周囲または距離です。, したがって、円の円周は円自体の完全な円弧であると言うことができます。
円弧の長さを見つける方法は?
円弧を計算するための式は、次のように述べています。
円弧の長さ=2nr(θ/360)
ここで、r=円の半径、
θ=pi=3.14
θ=円の中心で円弧でサブテンドされた角度(度)。
360=一つの完全な回転の角度。
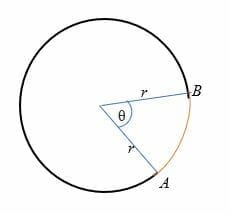
上の図から、円弧の長さ(赤で描かれている)は、点Aから点Bまでの距離です。,
円弧の長さに関するいくつかの例の問題を考えてみましょう:
例1
円弧ABが半径が40cmの円の中心に対して7度の角度を下げるとします。 円弧ABの長さを計算します。
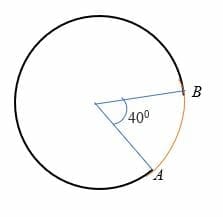
ソリューション
与えられたr=7cm
θ=40度。置換により、円弧の長さ=2nr(φ/360)
長さ=2×3.14x7x40/360
=4.884cm。
例2
半径が120cmの円の中心に対して24度の角度を持つ円の円弧の長さを求めます。,アークの長さ=2nr(φ/360)
=2×3.14x24x120/360
=50.24cm。
例3
円弧の長さは35mです。円の半径が14mの場合、円弧で囲まれた角度を見つけます。
解
円弧の長さ=2nr(π/360)
35m=2×3.14x14x(π/360)
35=87.92π/360
分数を取り除くために、両側に360を掛けます。
12600=87.92°
両側を87.92で割る
θ=143.3度。,
例4
長さ156cmの円弧の半径を求め、円の中心に対して150度の角度を下げます。
解
円弧の長さ=2nr(φ/360)
156cm=2×3.14x r x150/360
156=2.6167r
両側を2.6167
r=59.62cmで割ります。したがって、円弧の半径は59.62cmです。
円弧の長さをラジアンで見つける方法は?
ラジアン単位の円弧によってサブテンドされた角度と、円の半径に対する円弧の長さの比との間には関係があります。, この場合、
θ=(円弧の長さ)/(円の半径)である。したがって、ラジアン単位の円弧の長さは、
S=rθ
ここで、θ=ラジアン単位の円弧によってサブテンドされた角度
S=円弧の長さで与えられます。
r=円の半径。
一つのラジアンは、一つの半径の円弧長によってサブテンドされた中心角であり、すなわちs=r
ラジアンは、角度のサイズを測定するちょうど別の たとえば、角度を度からラジアンに変換するには、角度(度単位)にθ/180を掛けます。,
同様に、ラジアンを度に変換するには、角度(ラジアン単位)に180/πを掛けます
例5
半径が10cmで、サブテンド角度が0.349ラジアンの円弧の長さを求めます。アークの長さ=r≤
=0.349×10
=3.49cm。
例6
半径10m、角度2.356ラジアンの円弧の長さをラジアン単位で求めます。
ソリューション
円弧の長さ=r∞
=10m x2.356
=23.56m.
例7
長さ10.05mm、半径8mmの円弧でサブテンドされた角度を求めます。,
解
円弧の長さ=r≤
10.05=8≤
両側を8で割ります。
1.2567=θ
ここで、円弧によってサブテンシングされた角度は1.2567ラジアンです。
例8
円弧の長さが144ヤード、円弧の角度が3.665ラジアンの円の半径を計算します。
解
円弧の長さ=r≤
144=3.665r
両側を3.665で割ります。
144/3.665=r
r=39.29ヤード。
例9
半径が6.283cmの円の中心に対して角度が28ラジアンになる円弧の長さを計算します。,
解
円弧の長さ=r∞
=28×6.283
=175.93cm
マイナーアーク(h3)
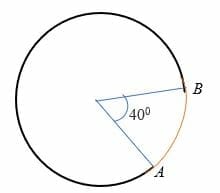
マイナーアークは、円の中心に対して180度以下の角度をサブテンダーする円弧です。 言い換えれば、マイナーアークは半円よりも小さい測定し、二つの点で円上に表されます。 たとえば、下の円の円弧ABはマイナー円弧です。
メジャーアーク(h3)
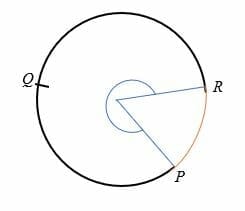
円のメジャーアークは、円の中心に対して180度以上の角度をサブテンダーする円弧です。, 主弧は半円よりも大きく、円上の三つの点で表されます。
たとえば、PQRは以下に示す円の主円弧です。
練習問題
- 半径9mmの円のセクターの面積を求めます。
- 都市Aは都市Bの真北にあります。都市Aと都市Bの緯度はそれぞれ54o Nと45o Nです。 両都市間の南北の距離は何ですか? 地球の半径は6400kmです。,