sen Jälkeen, kun säde ja halkaisija, toinen tärkeä osa ympyrän kaaren. Tässä artikkelissa, aiomme keskustella yksityiskohtaisesti, mitä kaari on, miten löytää pituus kaaren ja mittaus kaaren pituus radiaaneina. Tutkimme myös sivukaarta ja suurkaarta.
mikä on ympyrän kaari?
ympyrän kaari on mikä tahansa ympyrän kehän osa. Muistaakseni ympyrän kehä on kehä tai etäisyys ympyrän ympärillä., Siksi voimme sanoa, että ympyrän ympärysmitta on itse ympyrän täysi kaari.
Miten löytää kaaren pituus?
laskentakaava arc todetaan, että:
Arc pituus = 2nr (θ/360)
Missä, r = ympyrän säde,
π = pi = 3.14
θ = kulma (asteina) subtended jonka kaaren keskellä ympyrän.
360 = yhden täydellisen rotaation kulma.
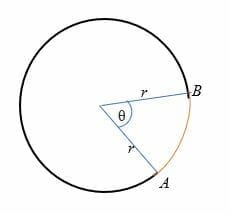
edellä kuvitus, pituus kaari (piirretty punaisella) on etäisyys pisteestä A pisteeseen B.,
tehdään muutama esimerkki ongelmista, pituus kaaren:
Esimerkki 1
ottaen Huomioon, että kaaren AB kaariminuutin kulmassa 40 astetta keskellä ympyrän, jonka säde on 7 cm. Laske arc AB: n pituus.
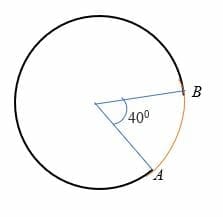
Ratkaisu
Koska r = 7 cm
θ = 40 astetta.
korvaamisen,
pituus kaari = 2nr(θ/360)
Pituus = 2 x 3.14 x 7 x 40/360
= 4.884 cm.
Esimerkki 2:
Löytää pituus kaaren ympyrän, joka kaariminuutin kulmassa 120 astetta keskellä ympyrän, jonka säde on 24 cm.,
Ratkaisu
pituus kaari = 2nr(θ/360)
= 2 x 3.14 x 24 x 120/360
= 50.24 cm.
Esimerkki 3.
pituus kaari on 35 m. Jos ympyrän säde on 14 m, löytää kulman subtended jonka kaari.
Ratkaisu
pituus kaari = 2nr(θ/360)
35 m = 2 x 3.14 x 14 x (θ/360)
35 = 87.92 θ/360
Kerrotaan molemmin puolin 360 poistaa murto-osa.
12600 = 87.92 θ
Jakaa molemmin puolin 87.92
θ = 143.3 astetta.,
Esimerkki 4.
Löytää säde kaaren, joka on 156 cm pitkä ja kaariminuutin kulmassa 150 astetta ympyrän keskipiste.
Ratkaisu
pituus kaari = 2nr(θ/360)
156 cm = 2 x 3.14 x r x 150/360
156 = 2.6167 r
Jakaa molemmin puolin 2.6167
r = 59.62 cm.
joten kaaren säde on 59,62 cm.
Miten Löytää Kaaren Pituus Radiaaneina?
välillä on suhde kulman subtended jonka kaaren radiaaneina ja suhde pituus kaaren ympyrän säde., Tällöin
θ = (kaaren pituus) / (ympyrän säde).
näin Ollen, pituus kaaren radiaaneina on antanut,
S = r θ
missä, θ = kulma subtended jonka kaaren radiaaneina
S = pituus kaari.
r = ympyrän säde.
Yksi radiaani on keski-kulman subtended jonka kaaren pituus on yksi säde eli s = r,
radiaani on vain toinen tapa mitata koko kulma. Esimerkiksi muunnettaessa kulmia asteista radiaaneiksi kerrotaan kulma (asteina) π/180: lla.,
voit Myös muuntaa radiaanit astetta, kerrotaan kulman (radiaaneina), jonka 180/π
Esimerkki 5.
Löytää pituus kaaren, jonka säde on 10 cm ja kulma subtended on 0.349 radiaaneina.
Ratkaisu
Arc pituus = r θ
= 0.349 x 10
= 3.49 cm.
Esimerkki 6.
Löytää pituus kaaren radiaaneina, joka on säde 10 m ja kulma 2.356 radiaaneina.
Ratkaisu
Arc pituus = r θ
= 10 m x 2.356
= 23.56 m.
Esimerkki 7.
Löytää kulman subtended jonka kaari, jonka pituus on 10.05 mm ja säde 8 mm.,
Ratkaisu
Arc pituus = r θ
10.05 = 8 θ
Jakaa molemmin puolin 8.
1.2567 = θ
Siellä kulman subtended jonka kaari on 1.2567 radiaaneina.
Esimerkki 8
Laske ympyrän säde, jonka kaaren pituus on 144 metriä ja arc kulma, on 3.665 radiaaneina.
Ratkaisu
Arc pituus = r θ
144 = 3.665 r
Jakaa molemmin puolin 3.665.
144/3.665 = r,
r = 39.29 metriä.
Esimerkki 9
Laske pituus kaaren, joka kaariminuutin kulmassa 6.283 radiaaneina keskellä ympyrä, joka on halkaisijaltaan 28 cm.,
Ratkaisu
Arc pituus = r θ
= 28 x 6.283
= 175.93 cm
Pieniä kaari (h3)
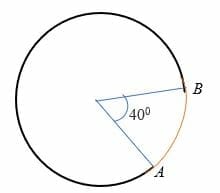
alaikäinen kaari on kaari, joka kaariminuutin kulmassa alle 180 astetta ympyrän keskipiste. Toisin sanoen, pieni kaari mittaa vähemmän kuin puoliympyrän ja on esitetty ympyrän kaksi pistettä. Esimerkiksi arc AB alla olevassa ympyrässä on mollikaari.
Suuret kaari (h3)
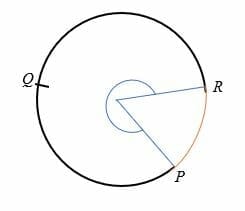
suuret kaari ympyrän kaari, joka kaariminuutin kulmassa enemmän kuin 180 astetta ympyrän keskipiste., Suuri kaari on suurempi kuin puoliympyrä ja sitä edustaa kolme pistettä ympyrän.
esimerkiksi PQR on alla olevan ympyrän pääkaari.
Käytännön Ongelmia
- Löytää alueen sektorin ympyrän säde 9 mm. Olettaa kulman subtended jonka tämä kaaren keskellä on 30 o.
- Kaupunki on Pohjoiseen kaupungin B. leveysasteilla kaupunki ja kaupungissa B on 54 o N ja 45 o N vastaavasti. Mikä on pohjoisen ja etelän välinen etäisyys näiden kahden kaupungin välillä? Maan säde on 6400 km.,