po poloměru a průměru je další důležitou součástí kruhu oblouk. V tomto článku budeme podrobně diskutovat o tom, co je oblouk, jak najít délku oblouku a měření délky oblouku v radiánech. Budeme také studovat o menším oblouku a velkém oblouku.
co je oblouk kruhu?
oblouk kruhu je jakákoli část obvodu kruhu. Chcete-li připomenout, obvod kruhu je obvod nebo vzdálenost kolem kruhu., Proto můžeme říci, že obvod kruhu je plný oblouk samotného kruhu.
jak najít délku oblouku?
vzorce pro výpočet oblouku se uvádí, že:
délka Oblouku = 2nr (θ/360)
, Kde r = poloměr kruhu,
π = pi = 3.14
θ = úhel (ve stupních) protilehlý oblouku ve středu kruhu.
360 = úhel jedné úplné rotace.
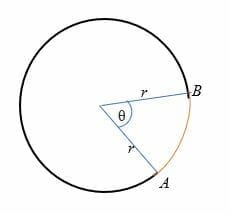
Z výše uvedeného obrázku, délka oblouku (nakreslené červeně) je vzdálenost z bodu A do bodu B.,
Pojďme vyřešit pár problémů například o délku oblouku:
Příklad 1
Vzhledem k tomu, že oblouk AB svírá úhel 40 stupňů do středu kruhu, jehož poloměr je 7 cm. Vypočítejte délku oblouku AB.
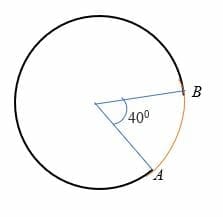
roztok
daný r = 7 cm
θ = 40 stupňů.
substitucí,
délka oblouku = 2NR (θ / 360)
délka = 2 x 3,14 x 7 x 40/360
= 4,884 cm.
Příklad 2
Najděte délku oblouku kružnice, který svírá úhel 120 stupňů do středu kruhu, jehož poloměr je 24 cm.,
Řešení
délka oblouku = 2nr(θ/360)
= 2 x 3.14 x 24 x 120/360
= 50.24 cm.
Příklad 3
délka oblouku je 35 m. Pokud poloměr kruhu je 14 m, najít úhel protilehlý oblouku.
Řešení
délka oblouku = 2nr(θ/360)
35 m = 2 x 3.14 x 14 x (θ/360)
35 = 87.92 θ/360
Vynásobte obě strany 360 odstranit zlomek.
12600 = 87.92 θ
rozdělte obě strany o 87.92
θ = 143.3 stupňů.,
Příklad 4
Najděte poloměr oblouku, který je 156 cm na délku a svírá úhel 150 stupňů do středu kruhu.
Řešení
délka oblouku = 2nr(θ/360)
156 cm = 2 x 3.14 x r x 150/360
156 = 2.6167 r
Rozdělte obě strany 2.6167
r = 59.62 cm.
poloměr oblouku je tedy 59,62 cm.
jak najít délku oblouku v radiánech?
Existuje vztah mezi úhel protilehlý oblouku v radiánech a poměr délky oblouku k poloměru kruhu., V tomto případě
θ = (délka oblouku) / (poloměr kruhu).
Proto, délka oblouku v radiánech je dána,
S = r θ
kde, θ = úhel protilehlý oblouku v radiánech
S = délka oblouku.
r = poloměr kružnice.
jeden radian je centrální úhel subtended o délce oblouku jednoho poloměru tj. s = r
radian je jen další způsob měření velikosti úhlu. Chcete-li například převést úhly ze stupňů na radiány, vynásobte úhel (ve stupních) π/180.,
Podobně, chcete-li převést radiány na stupně, vynásobte úhel (v radiánech) o 180/π
Příklad 5
Najděte délku oblouku, jehož poloměr je 10 cm a úhel protilehlý je vzduchu 0,349 radiánech.
roztok
délka oblouku = r θ
= 0, 349 x 10
= 3, 49 cm.
Příklad 6
Najděte délku oblouku v radiánech, který má poloměr 10 m a úhlu 2.356 radiánech.
Řešení
délka Oblouku = r θ
= 10 m x 2.356
= 23.56 m.
Příklad 7
Najděte úhel protilehlý oblouku, který má délku 10,05 mm a poloměru 8 mm.,
Řešení
délka Oblouku = r θ
10.05 = 8 θ
Vydělíme obě strany 8.
1.2567 = θ
tam je úhel podtržený obloukem 1.2567 radiánů.
příklad 8
Vypočítejte poloměr kružnice, jejíž délka oblouku je 144 yardů a úhel oblouku, je 3.665 radiánů.
řešení
délka oblouku = r θ
144 = 3.665 r
obě strany se dělí o 3.665.
144/3.665 = r
r = 39,29 yardů.
Příklad 9
Vypočítejte délku oblouku, který je protilehlý úhel 6.283 radiánech do středu kruhu, který má poloměr 28 cm.,
Řešení
délka Oblouku = r θ
= 28 x 6.283
= 175.93 cm
Menší oblouk (h3)
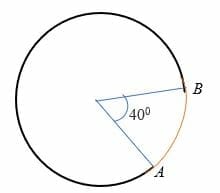
drobné arc je oblouk, který je protilehlý úhel z menší o 180 stupňů do středu kruhu. Jinými slovy, menší oblouk měří méně než půlkruh a je na kruhu reprezentován dvěma body. Například oblouk AB v níže uvedeném kruhu je menší oblouk.
Hlavní oblouk (h3)
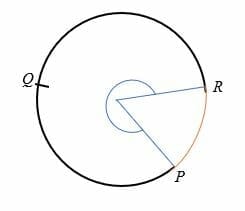
hlavní kruhový oblouk je oblouk, který je protilehlý úhel více než 180 stupňů do středu kruhu., Hlavní oblouk je větší než polokruh a je reprezentován třemi body na kruhu.
například PQR je hlavní oblouk níže uvedeného kruhu.
Problémy Praxe
- Najít oblast, odvětví kruhu o poloměru 9 mm. Předpokládejme, úhel protilehlý oblouk ve středu je 30 hodin.
- Město je na Sever od města. B. V zeměpisných šířkách město a a město B 54 N o a 45 o, N, resp. Jaká je severojižní vzdálenost mezi oběma městy? Poloměr Země je 6400 km.,